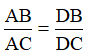nhận xét gì về các đường trung tuyến của 1 tam giác

Những câu hỏi liên quan
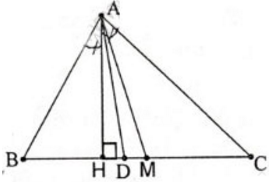
Cho tam giác ABC ( AB < AC). Vẽ đường cao AH, đường phân giác AD, đường trung tuyến AM. Có nhận xét gì về vị trí của ba điểm H, D, M.
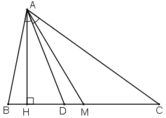
- Nhận xét: D luôn nằm giữa H và M.
- Chứng minh:

Đúng 0
Bình luận (0)
Cho tam giác ABC (AB < AC). Vẽ đường cao AH, đường phân giác AD, đường trung tuyến AM. Có nhận xét gì về vị trí của ba điểm H, D, M ?
- Nhận xét: D luôn nằm giữa H và M.
- Chứng minh:
Đúng 0
Bình luận (0)
Δ AMB và Δ AMC có: AM chung MB =MC và AC > AB
=> AMC^ > AMB^ => M thuộc CH.(M ở giữa C và H)
AB<AC => B^ > C^ => BAH^ < CAH^ => D thuộc CH.(1)
theo tính chất phân giác:
BD/AB = CD/AC
mà: AC > AB => CD > BD => D thuộc BM (2)
(1) và (2) => D thuộc HM hay D là điểm nằm giữa H và M.
Đúng 0
Bình luận (0)
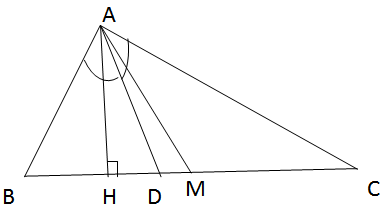
+Nhận xét: D luôn nằm giữa H và M.
+Chứng minh: AD là đường phân giác của ∆ABC.
=>ABAC=DBDCABAC=DBDC AB < AC
=>DB < DC => DB + DC < DC + DC
=>BD + DC < 2DC hay BC < 2DC => DC >BC2BC2
Mà MC=BC2MC=BC2 (M là trung điểm của BC)
=>DC > MC =>M nằm giữa D và C (1)
+Mặt khác: ˆCAH=900–^CCAH^=900–C^ (∆CAH vuông tại H)
^A+^B+^C=1800A^+B^+C^=1800 (tổng 3 góc ∆ABC)
=>ˆCAH=^A+^B+^C2–^CCAH^=A^+B^+C^2–C^
=>ˆCAH=^A2+^B2–^C2=^A2+^B–^C2CAH^=A^2+B^2–C^2=A^2+B^–C^2
Vì AB < AC =>ˆC<ˆB⇒ˆB–ˆC>0C^<B^⇒B^–C^>0
Do đó: ˆCAH>^A2CAH^>A^2 hay ˆCAH>ˆCADCAH^>CAD^
=>Tia AD nằm giữa hai tia AH và AC =>D nằm giữa hai điểm H và C (2)
Từ (1) và (2) => D nằm giữa H và M.
Đúng 0
Bình luận (0)
Cho tam giác ABC có AB < AC, phân giác AD,trung tuyến AM,đường cao AH.
a) So sánh độ dài của HB và HC
b) Chứng minh rằng HAC > \(\dfrac{A}{2}\)
c) Nhận xét gì về vị trí của các tia AH,AD,AM
a) Xét ΔABC có AB<AC(gt)
mà HB là hình chiếu của AB trên BC(gt)
và HC là hình chiếu của AC trên BC(gt)
nên HB<HC
c) tia AD nằm giữa hai tia AH và AM
Đúng 0
Bình luận (0)
trong tam giác đều Em có nhận xét về đường cao đường trung tuyến đường phân giác đường trung trực
Em hãy vẽ tam giác ABC đều vẽ các đường trung tuyến và xác định trọng tâm G của tam giác Do và nhận xét về đọ dài của các đoạn thẳng GA , GB, GC
tam giác ABC đều
=> AB=AC=BC
góc B = góc C= góc A
D,E,F là trung điểm BC,AC,AB
Xét tam giác ABD và ADC
AD chung
AB=AC
BD=DC
=> ABD=ACD (c.c.c)
=> góc ADB = góc ADC = 90 độ , góc BAD = góc CAD = 30 độ
tương tự ta có:
góc AFC =BFC, ACF=BCF=30
góc AEB=CEB, EBC = EBA=30
Xét tam giác AFG và tam giác BFG
góc AFG=BFG
AF=FB
góc FAG= FBG=30 độ
FG chung
=>tam giác AFG=BFG
=>AG=GB
tương tự cm tam giác AEG=CEG
=>AG=GC mà AG=GB
=>GA=GB=GC
Vậy ...
Đúng 0
Bình luận (0)
cho Tam giác có hai đg trung tuyến AD và BE cắt nhau ở G . Kéo dài GD thêm 1 đoạn DI DG . Kéo dài GE thêm 1 đoạn EK EG1) chứng minh AK ( CG ) BI 2) chứng minh AK // BG3) Chứng minh tam giác GAK Tam giác GIB và AG 2GD , BG 2GE4) Chứng minh DG DA : 3 , EG EB : 35) Nếu đường trung tuyến CF của Tam giác ABC cắt AD tại G thì ta có kết quả gì tương tự câu 4 ? Rút ra nhận xét về 3 đường trung tuyến .
Đọc tiếp
cho Tam giác có hai đg trung tuyến AD và BE cắt nhau ở G . Kéo dài GD thêm 1 đoạn DI = DG . Kéo dài GE thêm 1 đoạn EK = EG
1) chứng minh AK ( = CG ) = BI
2) chứng minh AK // BG
3) Chứng minh tam giác GAK = Tam giác GIB và AG = 2GD , BG = 2GE
4) Chứng minh DG = DA : 3 , EG = EB : 3
5) Nếu đường trung tuyến CF của Tam giác ABC cắt AD tại G thì ta có kết quả gì tương tự câu 4 ? Rút ra nhận xét về 3 đường trung tuyến .
1)
xét ΔAEK và Δ CEG có:
EA=EC(gt)
EG=EK(gt)
góc AEK= góc GEC( 2 góc đối đỉnh)
=> ΔAEK=ΔCEG(c.g.c)
=> AK=GC
cm tương tự ta có:ΔGDC=ΔIDB(c.g.c)
=> GC=BI
và AK=GC
=> AK=GC=BI
2)
theo câu a, ta có ΔAEK=ΔCEG(c.g.c)
=> góc EAK= góc ECG
=> AK//GC
theo câu a, ta có: ΔGDC=ΔIDB(c.g.c)
=> góc DGC= góc DIB
=> GC//BI
và AK//GC
=> AK//BI
3)
ta có: AD là đường trung tuyến ứng với cạnh BC của Δ ABC
BE là đường trung tuyến ứng với cạnh AC của ΔABC
=> giao của AD và BE là trọng tâm của ΔABC
=> G là trọng tâm của ΔABC
=> GA=2GD
mà GI=ID
=> GA=GI+ID=GI
ta có G là trọng tâm của ΔABC; BE là đường trung tuyến của ΔABC
=> BG=2GE
mà GE=EK
=> BG=GE+EK=GK
xét ΔGAK và ΔGIB có :
GA=GI(cmt)
GK=GB(cmt)
góc AGK= góc BGI(2 góc đối đỉnh)
=>ΔGAK=ΔGIB(c.g.c)
4)
ta có AD là đường trung tuyến của ΔABC
=> AD=3GD
hay DG=DA:3
ta có : BE là đường trung tuyến của ΔABC
=> GE=BE:3
5)
nếu CF là đường trung tuyến của ΔABC cắt AD tại G thì G là trọng tâm của tam giác ΔABC( tương tự như câu 4)
=> CG=2GF
NX: 3 đường trung tuyến của 1 tam giác cắt nhau tại 1 điểm. điểm này gọi là trọng tâm của tam giác đó
điểm này cách trung điểm của cạnh mà đoạn thẳng đi qua nó một khoảng =1/2 k/cách từ điểm đó đến đỉnh của tam giác mà đoạn thẳng đã đi nó
Đúng 0
Bình luận (0)
cho tam giác ABC có AB<AC . phân giác AD trung tuyến AM, đường cao AH
a) so sánh HB và HC
b) CMR góc HAC> A/2
c) nhận xét gì về vị trí các tia AH, AD, AM
Giúp mình với:
Bài 1:Cho tam giác ABC.Vẽ đường phân giác Ax,By,Cz lần lượt của góc A,góc B,góc C.Có nhận xét gì về quan hệ gì giữa ba đường Ax,By,Cz.
Bài 2:Cho tam giác ABC.N là trung điểm của BC.M là trung điểm AB,B là trung điểm AC,có nhận xết gì giữa ba đoạn thẳng AN,CM,BP.
Vẽ tam giác ABC cân tại A vẽ các đường trung tuyến,đường phan giác,đường trung trực xuất phát từ đỉnh A tới cạnh đối diện rút ra nhận xét
Chưa học nên chưa biết, xin lỗi bạn nhé tớ chưa học dạng toán hình học này!
Đúng 0
Bình luận (0)
Ta thấy các đường trung tuyến đường phân giác, đường trung trực xuất phát từ A tới cạnh đối diện trùng nhau .
Đúng 1
Bình luận (0)
Các đường trung tuyến, đường phân giác và đường trung trực xuất phát từ đỉnh A đến cạnh đối diện trùng nhau
Đúng 0
Bình luận (0)
Hãy vẽ hình tam giác ABC có ba góc nhọn rồi vẽ đường cao AD,BE,CG của hình tam giác đó . Em có nhận xét gì về các đường cao AD,BE,CG của hình tam giác này
Ba đường này cắt nhau tại một điểm gọi là trực tâm của tam giác
Đúng 0
Bình luận (0)