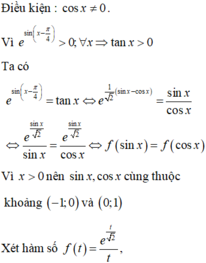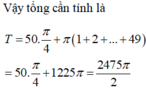Tính tổng các nghiệm nguyên thuộc [-5;5] của bất phương trình \(\sqrt{x^2-9}\left(\frac{3x-1}{x+5}\right)\le x\sqrt{x^2-9}\)

Những câu hỏi liên quan
Tính tổng S của tất cả các giá trị nguyên của m để bất phương trình
ln
7
x
2
+
7
≥
ln
m
x
2
+
4
x
+
m
nghiệm đúng với mọi x thuộc R A. S 12 B. S 14 C. S 35 D. S...
Đọc tiếp
Tính tổng S của tất cả các giá trị nguyên của m để bất phương trình ln 7 x 2 + 7 ≥ ln m x 2 + 4 x + m nghiệm đúng với mọi x thuộc R
A. S = 12
B. S = 14
C. S = 35
D. S = 0
Gọi S là tập hợp các nghiệm thuộc đoạn
0
;
2
π
của phương trình
sin
2
x
+
3
cos
2
x
−
2
. Biết rằng tổng các phần tử thuộc S bằng
m
π
n
, trong đó m, n là các số nguyên dương và phân số
m...
Đọc tiếp
Gọi S là tập hợp các nghiệm thuộc đoạn 0 ; 2 π của phương trình sin 2 x + 3 cos 2 x = − 2 . Biết rằng tổng các phần tử thuộc S bằng m π n , trong đó m, n là các số nguyên dương và phân số m n tối giản. Tính T = 22 m + 6 n + 2018 .
A. T = 2322
B. T = 2340
C. T = 2278
D. T = 2388
Đáp án A.
Ta có
sin 2 x + 3 cos 2 x = − 2 ⇔ cos 2 x − π 6 = − 2 2 .
⇔ x = − 7 π 24 + k π hoặc x = 11 π 24 + k π , k ∈ ℤ .
Nghiệm thuộc đoạn 0 ; 2 π của phương trình là 11 π 24 ; 17 π 24 ; 35 π 24 ; 41 π 24 .
Suy ra S = 11 π 24 ; 17 π 24 ; 35 π 24 ; 41 π 24 .
Do đó tổng các phần tử thuộc S là
11 π 24 + 17 π 24 + 35 π 24 + 41 π 24 = 104 24 π + 13 3 π
Ta có m=13 và n=3 nên T=2322.
Đúng 0
Bình luận (0)
Gọi S là tập hợp các nghiệm thuộc đoạn
0
;
2
π
của phương trình
sin
2
x
+
3
cos
2
x
−
2
. Biết rằng tổng các phần tử thuộc S bằng
m
π
n
, trong đó m, n là các số nguyên dương và phân số
m...
Đọc tiếp
Gọi S là tập hợp các nghiệm thuộc đoạn 0 ; 2 π của phương trình sin 2 x + 3 cos 2 x = − 2 . Biết rằng tổng các phần tử thuộc S bằng m π n , trong đó m, n là các số nguyên dương và phân số m n tối giản. Tính T=22m+6n+2018.
A. T=2322
B. T=2340
C. T=2278
D. T=2388
Tính tổng tất cả các giá trị \(m\) nguyên để phương trình \(mcos2x=\dfrac{cos^4x-sin^4x}{sinx}\) có đúng 4 nghiệm phân biệt thuộc \(\left(0;2\pi\right)\).
A. 1
B. 2
C. 3
D. 0
Gọi S là tập hợp tất cả các giá trị nguyên của tham số m thuộc đoạn [−5; 10] để phương trình
m
+
1
x
3
m
2
-
1
x
+
m
-
1
có nghiệm duy nhất. Tổng các phần tử trong S bằng: A. 15 B. 39 C. 17 D. 40
Đọc tiếp
Gọi S là tập hợp tất cả các giá trị nguyên của tham số m thuộc đoạn [−5; 10] để phương trình m + 1 x = 3 m 2 - 1 x + m - 1 có nghiệm duy nhất. Tổng các phần tử trong S bằng:
A. 15
B. 39
C. 17
D. 40
Phương trình viết lại m + 1 x = 3 m 2 - 1 x = 1 - m
Phương trình đã cho có nghiệm duy nhất khi 3 m 2 - m - 2 ≠ 0 ⇔ m ≠ 1 m ≠ − 2 3
Do m ∈ Z và m ∈ [−5; 10] ⇒ m ∈ {−5; −4; −3; −2; −1; 0; 2; 3; 4; 5; 6; 7; 8; 9; 10}.
Do đó, tổng các phần tử trong S bằng 39.
Đáp án cần chọn là: B
Đúng 0
Bình luận (0)
A={x thuộc Z/-6<x<5} =
a)tính tổng S các số nguyên x thuộc a
Các bạn giải giúp mình với
Cho tập hợp A={ x thuộc Z / -5 < x < 5 }
a) Viết A dưới dạng liệt kê các phần tử:
b) Tính tổng các số nguyên x thuộc A
a) A = {-4; -3; -2; -1; 0; 1; 2; 3; 4}
b) Tổng các số nguyên x thuộc A là
-4 + (-3) + (-2) + (-1) + 0 + 1 + 2 + 3 + 4 = (-4 + 4) + (-3 + 3) + (-2 + 2) + (-1 + 1) + 0 = 0 + 0 + 0 + 0 + 0 = 0
Đúng 0
Bình luận (0)
Cho tập hợp A={ x thuộc Z/ -5 < x < 5}
a/ Viết A dưới dạng liệt kê các phần tử
b/ Tính tổng các số nguyên x thuộc A
a ) A = { - 4 ; - 3 ; - 2 ; - 1 ; 0 ; 1 ; 2 ; 3 ; 4 }
Tổng các số nguyên x là : - 4 + ( - 3 ) + ( - 2 ) + ( - 1 ) + 0 + 1 + 2 + 3 + 4 = 0
Đúng 0
Bình luận (0)
a) A={-4;-3;-2;-1;0;1;2;3;4}
b) Ta thấy: -4 là số đối của 4
-3 là số đối của 3
-2 là số đối của 2
-1 là số đối của 1
từ đó suy ra: Tổng của A= (-4)+(-3)+(-2)+(-1)+0+1+2+3+4 = 0
Đúng 0
Bình luận (0)
jqn4hunhwnbjnwgjubusnowrnjrnfnnrinjiwrnmiwnirt ọe
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
Tính tổng tất cả các nghiệm của phương trình
e
sin
x
−
π
4
tan
x
thuộc
0
;
50
π
A.
1853
π...
Đọc tiếp
Tính tổng tất cả các nghiệm của phương trình e sin x − π 4 = tan x thuộc 0 ; 50 π
A. 1853 π 2
B. 2475 π 2
C. 2671 π 2
D. 1853 π 2
Tính tổng S là tổng các nghiệm thuộc đoạn
0
;
2
π
của phương trình:
sin
2
x
+
9
π
2
−
3
cos
x
−...
Đọc tiếp
Tính tổng S là tổng các nghiệm thuộc đoạn 0 ; 2 π của phương trình:
sin 2 x + 9 π 2 − 3 cos x − 15 π 2 = 1 + 2 sin x I
A. S = 4 π
B. S = 2 π
C. S = 3 π
D. S = 5 π
Đáp án A
Ta có sin 2 x + 9 π 2 = sin 2 x + π 2 + 4 π = cos 2 x và cos x − 15 π 2 = − sin x
Khi đó, phương trình (I) ⇔ cos 2 x + 3 sin x = 1 + 2 sin x ⇔ 1 − 2 sin 2 x = 1 − sin x ⇔ sin x = 0 sin x = 1 2
Kết hợp với x ∈ 0 ; 2 π , ta được x = 0 ; π ; 2 π ; π 6 ; 5 π 6 là các nghiệm của phương trình
Đúng 0
Bình luận (0)