Đáp án A

Phương pháp:

Cô lập m, đưa về dạng f(x) = m

Số nghiệm của phương trình là số giao điểm của đồ thị hàm số y = f(x) và đường thẳng y = m

Cách giải:

Điều kiện: x ≠ 2, x ≠ -4

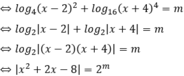
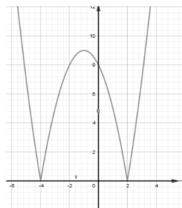
Số nghiệm của phương trình đã cho bằng số giao điểm của đồ thị hàm số y = |x2 + 2x - 8| và đường thẳng y = 2m

Quan sát đồ thị hàm số bên, ta thấy, để đồ thị hàm số y = |x2 + 2x - 8| cắt đường thẳng y = 2m tại 4 điểm phân biệt thì 0 < 2m < 9 ⇔ m < log29 ⇔ m < 2 log23

\(\text{Δ}=\left(-8\right)^2-4\cdot\left(-3\right)\cdot\left(m-1\right)\)

\(=64+12\left(m-1\right)\)

=64+12m-12

=12m+52

a: Để phương trình có hai nghiệm phân biệt nhỏ hơn 7 thì 

\(\left\{{}\begin{matrix}12m+52>0\\8< 14\end{matrix}\right.\Leftrightarrow m>-\dfrac{13}{4}\)

b: Để phương trình có hai nghiệm phân biệt lớn hơn 7 thì \(\left\{{}\begin{matrix}12m+52>0\\8>14\end{matrix}\right.\Leftrightarrow m\in\varnothing\)

mình làm luôn 4 nghiệm nhé-đổi k thành m cho dễ nhé

Pt trở thành: t² + 2mt + 4 = 0 (*). 
Pt đã cho có 4 nghiệm phân biệt <=> pt (*) có 2 nghiệm phân biệt dương. => xảy ra đồng thời: delta’(t) > 0; S = x1 + x2 > 0; p = x1x2 > 0 <=> m² - 4 > 0; -2m > 0; 4 > 0 ( theo Vi-et) 
=> m < -2. 
=> pt đã cho có nghiệm x1,2 = +- căn t1; x3,4 = +- căn t2 
=> x1^4 = x2^4 = t1²; x3^4 = x4^4 = t2² 
=> x1^4 + x2^4 + x3^4 + x4^4 = 2(t1² + t2²) = 32 => t1² + t2² = 16. 
<=> (t1 + t2)² - 2t1t2 = 16 <=> (-2m)² - 2.4 = 16 <=> 4m² - 4 = 16 
<=> m² = 6, mà m < -2 => m = -(căn 6). 
vậy với m = -(căn 6) thì pt đã cho có 4 nghiệm phân biệt x1 ,x2, x3, x4 thỏa mãn x1^4 + x2^4 + x3^4 + x4^4 = 32. 

mik lm 4 nghiệm nhé-đổi k thành m nữa

Pt trở thành: t² + 2mt + 4 = 0 (*). 
Pt đã cho có 4 nghiệm phân biệt <=> pt (*) có 2 nghiệm phân biệt dương. => xảy ra đồng thời: delta’(t) > 0; S = x1 + x2 > 0; p = x1x2 > 0 <=> m² - 4 > 0; -2m > 0; 4 > 0 ( theo Vi-et) 
=> m < -2. 
=> pt đã cho có nghiệm x1,2 = +- căn t1; x3,4 = +- căn t2 
=> x1^4 = x2^4 = t1²; x3^4 = x4^4 = t2² 
=> x1^4 + x2^4 + x3^4 + x4^4 = 2(t1² + t2²) = 32 => t1² + t2² = 16. 
<=> (t1 + t2)² - 2t1t2 = 16 <=> (-2m)² - 2.4 = 16 <=> 4m² - 4 = 16 
<=> m² = 6, mà m < -2 => m = -(căn 6). 
vậy với m = -(căn 6) thì pt đã cho có 4 nghiệm phân biệt x1 ,x2, x3, x4 thỏa mãn x1^4 + x2^4 + x3^4 + x4^4 = 32. 

a, Thay m = -1 vào phương trình trên ta được 

\(x^2+4x-5=0\)

Ta có : \(\Delta=16+20=36\)

\(x_1=\frac{-4-6}{2}=-5;x_2=\frac{-4+6}{2}=1\)

Vậy với m = -1 thì x = -5 ; x = 1 

b, Vì x = 2 là nghiệm của phương trình trên nên thay x = 2 vào phương trình trên ta được : 

\(4+8+3m-2=0\Leftrightarrow3m=-10\Leftrightarrow m=-\frac{10}{3}\)

Vậy với x = 2 thì m = -10/3 

c, Để phương trình có 2 nghiệm phân biệt thì \(\Delta>0\)hay 

\(16-4\left(3m-2\right)=16-12m+8=4m+8>0\)

\(\Leftrightarrow8>-4m\Leftrightarrow m>-2\)

Theo Vi et ta có : \(\hept{\begin{cases}x_1+x_2=-\frac{b}{a}=-4\\x_1x_2=\frac{c}{a}=3m-2\end{cases}}\)

\(\Leftrightarrow x_1+x_2=-4\Leftrightarrow x_1=-4-x_2\)(1) 

suy ra : \(-4-x_2+2x_2=1\Leftrightarrow-4+x_2=1\Leftrightarrow x_2=5\)

Thay vào (1) ta được : \(x_1=-4-5=-9\)

Mà \(x_1x_2=3m-2\Rightarrow3m-2=-45\Leftrightarrow3m=-43\Leftrightarrow m=-\frac{43}{3}\)

Đáp án B

1.

Đặt \(\sqrt{x^2-4x+5}=t\ge1\Rightarrow x^2-4x=t^2-5\)

Pt trở thành:

\(4t=t^2-5+2m-1\)

\(\Leftrightarrow t^2-4t+2m-6=0\) (1)

Pt đã cho có 4 nghiệm pb khi và chỉ khi (1) có 2 nghiệm pb đều lớn hơn 1

\(\Leftrightarrow\left\{{}\begin{matrix}\Delta'=4-\left(2m-6\right)>0\\\left(t_1-1\right)\left(t_2-1\right)>0\\\dfrac{t_1+t_2}{2}>1\\\end{matrix}\right.\)

\(\Leftrightarrow\left\{{}\begin{matrix}10-2m>0\\t_1t_2-\left(t_1+t_1\right)+1>0\\t_1+t_2>2\end{matrix}\right.\)

\(\Leftrightarrow\left\{{}\begin{matrix}m< 5\\2m-6-4+1>0\\4>2\end{matrix}\right.\) \(\Leftrightarrow\dfrac{9}{2}< m< 5\)

2.

Để pt đã cho có 2 nghiệm:

\(\Leftrightarrow\left\{{}\begin{matrix}m\ne3\\\Delta'=1+4\left(m-3\right)\ge0\end{matrix}\right.\)

\(\Leftrightarrow\left\{{}\begin{matrix}m\ne3\\m\ge\dfrac{11}{4}\end{matrix}\right.\)

Khi đó:

\(x_1^2+x_2^2=4\Leftrightarrow\left(x_1+x_2\right)^2-2x_1x_2=4\)

\(\Leftrightarrow\dfrac{4}{\left(m-3\right)^2}+\dfrac{8}{m-3}=4\)

\(\Leftrightarrow\dfrac{1}{\left(m-3\right)^2}+\dfrac{2}{m-3}-1=0\)

\(\Leftrightarrow\left[{}\begin{matrix}\dfrac{1}{m-3}=-1-\sqrt{2}\\\dfrac{1}{m-3}=-1+\sqrt{2}\end{matrix}\right.\)

\(\Leftrightarrow\left[{}\begin{matrix}m=4-\sqrt{2}< \dfrac{11}{4}\left(loại\right)\\m=4+\sqrt{2}\end{matrix}\right.\)

3.

Nối AI kéo dài cắt BC tại D thì D là chân đường vuông góc của đỉnh A trên BC

\(\Rightarrow\dfrac{DB}{DC}=\dfrac{AB}{AC}=\dfrac{c}{b}\)

\(\Rightarrow\overrightarrow{BD}=\dfrac{c}{b}\overrightarrow{DC}\)

\(\Leftrightarrow\overrightarrow{ID}-\overrightarrow{IB}=\dfrac{c}{b}\left(\overrightarrow{IC}-\overrightarrow{ID}\right)\)

\(\Leftrightarrow b.\overrightarrow{IB}+\overrightarrow{c}.\overrightarrow{IC}=\left(b+c\right)\overrightarrow{ID}\) (1)

Mặt khác:

\(\dfrac{ID}{IA}=\dfrac{BD}{AB}=\dfrac{CD}{AC}=\dfrac{BD+CD}{AB+AC}=\dfrac{BC}{AB+AC}=\dfrac{a}{b+c}\)

\(\Leftrightarrow\left(b+c\right)\overrightarrow{ID}=-a.\overrightarrow{IA}\) (2)

(1); (2) \(\Rightarrow a.\overrightarrow{IA}+b.\overrightarrow{IB}+c.\overrightarrow{IC}=\left(b+c\right)\overrightarrow{ID}-\left(b+c\right)\overrightarrow{ID}=\overrightarrow{0}\)

Lời giải:

Xin chỉnh sửa lại chút, tìm $k$, chứ không phải tìm $m$.

PT $\Leftrightarrow x^2-(6k-2)=0\Leftrightarrow x^2=6k-2$

Để pt có 2 nghiệm phân biệt thì $6k-2>0\Leftrightarrow k>\frac{1}{3}$

Khi đó:

$x_1=\sqrt{6k-2}$ và $x_2=-\sqrt{6k-2}$

Để $3x_1-x_2=2$

$\Leftrightarrow 3\sqrt{6k-2}+\sqrt{6k-2}=2$

$\Leftrightarrow \sqrt{6k-2}=\frac{1}{2}\Rightarrow k=\frac{3}{8}$