a) tìm m để (P) \(y=3x^2\) và (d) y=5x+2m-1 có điểm chung b) Hãy tính giá trị của biểu thức \(A=x_1^3+x_2^3-5x_1x_2\)
1) a) Tính giá trị của biểu thức \(\sqrt{\left(\sqrt{3}-2\right)^2}\)+\(\sqrt{3}\)
b) Tìm các giá trị của tham số m để hai đường thẳng (d):y=(m+2).x-m (m≠-2) và (d'):y = -2x-2m+1 cắt nhau.
c) Tìm hệ số góc của đường thẳng (d):y=(2m-3)x+m ( với m≠\(\dfrac{3}{2}\)) biết (d) đi qua điểm A (3;-1)
a) √(√3 - 2)² + √3
= 2 - √3 + √3
= 2
b) Để (d) và (d') cắt nhau thì:
m + 2 ≠ -2
m ≠ -2 - 2
m ≠ -4
Vậy m ≠ -4 thì (d) cắt (d')
c) Thay tọa độ điểm A(3; -1) vào (d) ta có:
(2m - 3).3 + m = -1
⇔ 6m - 9 + m = -1
⇔ 7m = -1 + 9
⇔ 7m = 8
⇔ m = 8/7 (nhận)
Thay m = 8/7 vào (d) ta có:
(d): y = -5x/7 - 8/7
Vậy hệ số góc của (d) là -5/7
cho hàm số y=2m-3x+n-4 (d)
a,tìm giá trị của m và n để (d) đi qua A (1;2) và B(3;4)
b,Cắt trục hoành có hoành độ x=1+căn 2
cắt trục tung tại điểm có tung độ y=3 căn 2-1
Cho hàm số bậc nhất y=(2m-1)x-2m+5(m là tham số) có đồ thị là đường thẳng (d) và hàm số y=2x+1 có đồ thị là đường thẳng (d')
a. tìm giá trị của m để đường thẳng(d) đi qua điểm A(2;-3)
b. tìm giá trị của m để đường thẳng(d) song song với đường thẳng (d') .với giá trị m vừa tìm được ,vẽ đường thẳng(d) và tính góc α tạo bởi đường thẳng (d) và trục Ox ( làm tròn đến phút)
a: Thay x=2 và y=-3 vào (d), ta được:
\(2\left(2m-1\right)-2m+5=-3\)
=>\(4m-2-2m+5=-3\)
=>2m+3=-3
=>2m=-6
=>\(m=-\dfrac{6}{2}=-3\)
b: Để (d)//(d') thì \(\left\{{}\begin{matrix}2m-1=2\\-2m+5\ne1\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}2m=3\\-2m\ne-4\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}m=\dfrac{3}{2}\\m\ne2\end{matrix}\right.\)
=>m=3/2
Thay m=3/2 vào (d), ta được:
\(y=\left(2\cdot\dfrac{3}{2}-1\right)x-2\cdot\dfrac{3}{2}+5=2x+2\)

y=2x+2 nên a=2
Gọi \(\alpha\) là góc tạo bởi (d) với trục Ox
\(tan\alpha=2\)
=>\(\alpha\simeq63^026'\)
Cho hàm số y=(2m-3)x-1. a) tìm giá trị của m để đồ thị hàm số song song với đường hẳng y=-5x+3. Vẽ đồ thị. b) Tìm giá trị của m để đồ thị hàm số đi qua điểm A(-1;0). c) Tìm giá trị của m để đồ thị của hàm số đã cho và các bạn các đường thẳng y=1 và y=2x-5 đồng qui tại một điểm. Giúp mình giải bài này với.
a)Vẽ đồ thị hàm số y=2x+2
b)Tìm giá trị của m để đồ thị hàm số y=3x+(2-m)và y=x+(2m-1) tại mọi điểm trên trục tung
a) Bạn tự vẽ
b) Để 2 đồ thị hàm số cắt nhau tại 1 điểm trên trục tung
\(\Leftrightarrow\left\{{}\begin{matrix}3\ne1\\2-m=2m-1\end{matrix}\right.\) \(\Leftrightarrow m=1\)
Vậy \(m=1\)
cho hàm số:y=(m-1)x+2m-5 (d)
a)tìm giá trị của m để hàm số trên là hàm số đồng biến
b)tìm giá trị của m để đường thẳng (d) đi qua điểm M(2;1)
c)tìm giá trị của m để đường thẳng (d)//với đường thẳng y=3x+1
d)tìm giá trị của m để đường thẳng (d) cắt đường thẳng y=2x+3 tại 1 điểm trên trục tung
e)CMR: đường thẳng (d) luôn luôn đi qua 1 điểm cố định khi m thay đổi
a) Để hàm số đồng biến thì a>0 => m-1>0 <=> m>1
b) Thay M(2;1) vào h/s
1=(m-1).2+2m-5 => m=2
c) Để d song song với đường thẳng trên thì a=a' \(m-1=3\Leftrightarrow m=4\)
d) Cắt 1 điểm trên trục tung thì b=b' \(\Leftrightarrow2m-5=3\Leftrightarrow m=4\)
Tiếp tục với bài của bạn Elza Julius Ruventaren
e) Gọi điểm cố định là \(M\left(x_0;y_0\right)\)
\(\Leftrightarrow\left(m-1\right)x_0+2m-5=y_0\) \(\left(\forall m\right)\)
\(\Leftrightarrow mx_0-x_0+2m-5=y_0\) \(\left(\forall m\right)\)
\(\Leftrightarrow m\left(x_0+2\right)=y_0+x_0+5\) \(\left(\forall m\right)\)
\(\Leftrightarrow\left\{{}\begin{matrix}x_0+2=0\\y_0+x_0+5=0\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}x_0=-2\\y_0=-3\end{matrix}\right.\)
Vậy (d) luôn đi qua điểm cố định \(\left(-2;-3\right)\)
cho đường thẳng (d) có phương trình y = (2m - 1)x + m + 1 và đường thẳng (d') có phương trình y = x+ 3
a, tính giá trị của m để đường thẳng (d) cắt đường thẳng (d') tại một điểm trên trục tung
b, tìm m để khoản cách từ gốc tọa độ O đến dường thẳng (d) đạt giá trị lớn nhất và giá trị lớn nhất đó bằng nhau
Bài 8: Cho hàm số y=(2m-1)x+3 (d). Đi I) Vẽ đồ thị hàm số khi m=\frac{3}{2}
2) Tính góc tạo bởi đường thẳng d với trục Ox
3) Tìm giá trị của m để (d) song song với đường thẳng y=3x+1(d^{\prime}) .
4) Tìm m để (d) cắt (d1) y=2x-3 tại điểm có hoành độ bằng 1
5) Tìm m để (d) cắt (d2) y=2x-3 tại điểm có tung độ bằng 1
6) Gọi hai điểm A, B lần lượt là giao điểm của (d) với trục Ox và Oy. Tìm m để diện tích tam giác OAB bằng 3 (đvdt)
7) Tìm m để khoảng cách từ gốc tọa độ O đến d là lớn nhất.
Em cần gấp ạ
1: Khi m=3/2 thì \(\left(d\right):y=\left(2\cdot\dfrac{3}{2}-1\right)x+3=2x+3\)
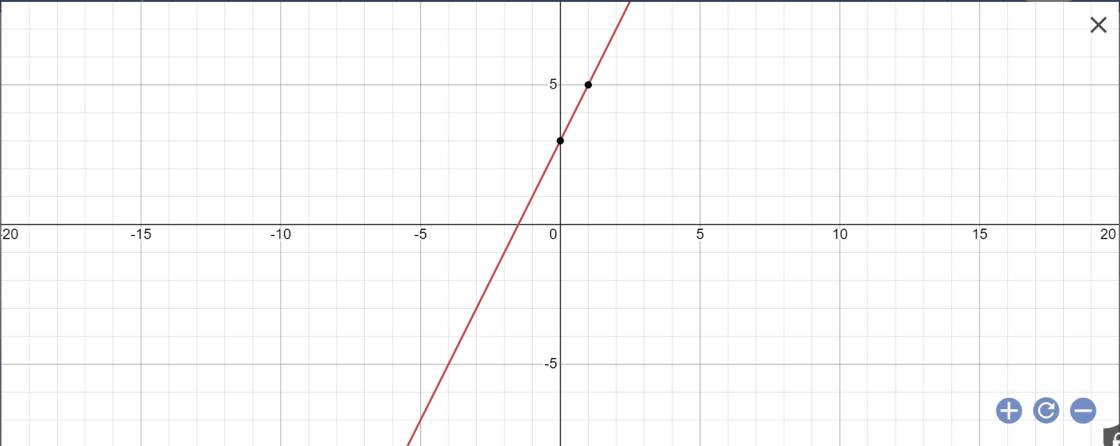
2: \(tanx=a=2m-1\)
3:
Để hai đồ thị (d) và (d') song song với nhau thì:
\(2m-1=3\)
=>2m=4
=>m=2
4: Thay x=1 vào (d1), ta được:
\(y=2\cdot1-3=-1\)
Thay x=1 và y=-1 vào (d), ta được:
\(1\left(2m-1\right)+3=-1\)
=>2m+2=-1
=>2m=-3
=>\(m=-\dfrac{3}{2}\)
5: y=1
=>2x-3=1
=>2x=4
=>x=2
Thay x=2 và y=1 vào (d),ta được:
\(2\left(2m-1\right)+3=1\)
=>2(2m-1)=-2
=>2m-1=-1
=>2m=0
=>m=0
Cho hàm số (C): y = x 3 - 6 x 2 + 9 x và đường thẳng d: y = 2 m - m 2 . Tìm số giá trị của tham số thực m để đường thẳng d và đồ thị (C) có hai điểm chung
A. 4
B. 3
C. 2.
D. Vô số
Đáp án C
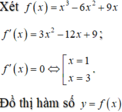

Đồ thị hàm số y = f ( x ) gồm hai phần:
Phần 1. Giữ nguyên phần đồ thị nằm phía trên trục hoành.
Phần 2. Lấy đối xứng phần nằm dưới trục hoành qua trục hoành

Dựa vào đồ thị, ta thấy đường thẳng d và đồ thị (C) có hai điểm chung khi
