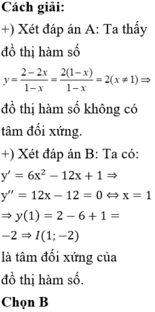Tâm đối xứng của đồ thị hàm số y=\(\frac{5x+1}{x-1}\)là điểm nào trong các điểm có tọa độ dưới đây
Những câu hỏi liên quan
Tâm đối xứng của đồ thị hàm số
y
3
x
−
3
x
+
1
là điểm I có tọa độ A.
I
3
;
−
1
B.
I
1
;
−
1...
Đọc tiếp
Tâm đối xứng của đồ thị hàm số y = 3 x − 3 x + 1 là điểm I có tọa độ
A. I 3 ; − 1
B. I 1 ; − 1
C. I − 1 ; 3
D. I − 1 ; − 3
Đáp án C
Tâm đối xứng là giao điểm 2 tiệm cận.
Đúng 0
Bình luận (0)
Đồ thị hàm số nào dưới đây có tâm đối xứng là điểm I(1;-2)? A. . B. . C. . D. .
Đọc tiếp
Đồ thị hàm số nào dưới đây có tâm đối xứng là điểm I(1;-2)?
A. 
.
B. 
.
C. 
.
D. 
.
+) Xét đáp án A: Ta thấy đồ thị hàm số 
đồ thị hàm số không có tâm đối xứng.
+) Xét đáp án B:
Ta có: 
là tâm đối xứng của đồ thị hàm số.
Chọn B
Đúng 0
Bình luận (0)
Đồ thị hàm số nào dưới đây có tâm đối xứng là điểm I(1;-2)?
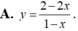
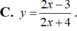
Hàm số nào dưới đây có đồ thị nhận gốc tọa độ làm tâm đối xứng?
Cho hàm số
y
x
−
2
x
+
1
. Xét các phát biểu sau đây+) Đồ thị hàm số nhận điểm
I
−
1
;
1
làm tâm đối xứng.+) Hàm số đồng biến trên tập
ℝ
−
1
.+) Giao điểm của...
Đọc tiếp
Cho hàm số y = x − 2 x + 1 . Xét các phát biểu sau đây
+) Đồ thị hàm số nhận điểm I − 1 ; 1 làm tâm đối xứng.
+) Hàm số đồng biến trên tập ℝ \ − 1 .
+) Giao điểm của đồ thị với trục hoành là điểm A 0 ; − 2
+) Tiệm cận đứng là y = 1 và tiệm cận ngang là x = − 1
Trong các phát biểu trên, có bao nhiêu phát biểu đúng?
A. 1
B. 3
C. 2
D. 4
Đồ thị hàm số nào dưới đây nhận gốc tọa độ làm tâm đối xứng?
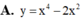
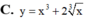
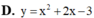
Đồ thị hàm số nào dưới đây nhận gốc tọa độ làm tâm đối xứng?
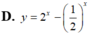
Tọa độ tâm đối xứng của đồ thị hàm số
y
x
-
2
2
x
-
1
là A.
-
1
2
;
2
B.
1
2
;...
Đọc tiếp
Tọa độ tâm đối xứng của đồ thị hàm số y = x - 2 2 x - 1 là
A. - 1 2 ; 2
B. 1 2 ; 1 2
C. 1 2 ; - 1
D. - 1 2 ; 1 2
Chọn B.
Tâm đối xứng của đồ thị hàm số này là giao điểm của 2 đường tiệm cận 1 2 ; 1 2
Đúng 0
Bình luận (0)
Cho hai hàm số y dfrac{1}{2}x^2 và y x2.a.Vẽ đồ thị của hai hàm số này trên cùng mặt phẳng tọa độ .b.Tìm tọa độ hai điểm A ; B có cùng hoành độ x 2 theo thứ tự nằm trên hai đồ thị .c.Gọi A’ và B’ lần lượt là các điểm đối xứng với A ; B qua trục tung Oy . Kiểm tra xem A’ ; B’ có lần lượt nằm trên hai đồ thị đó không ?
Đọc tiếp
Cho hai hàm số y = \(\dfrac{1}{2}x^2\) và y = x2.
a.Vẽ đồ thị của hai hàm số này trên cùng mặt phẳng tọa độ .
b.Tìm tọa độ hai điểm A ; B có cùng hoành độ x = 2 theo thứ tự nằm trên hai đồ thị .
c.Gọi A’ và B’ lần lượt là các điểm đối xứng với A ; B qua trục tung Oy . Kiểm tra xem A’ ; B’ có lần lượt nằm trên hai đồ thị đó không ?
a: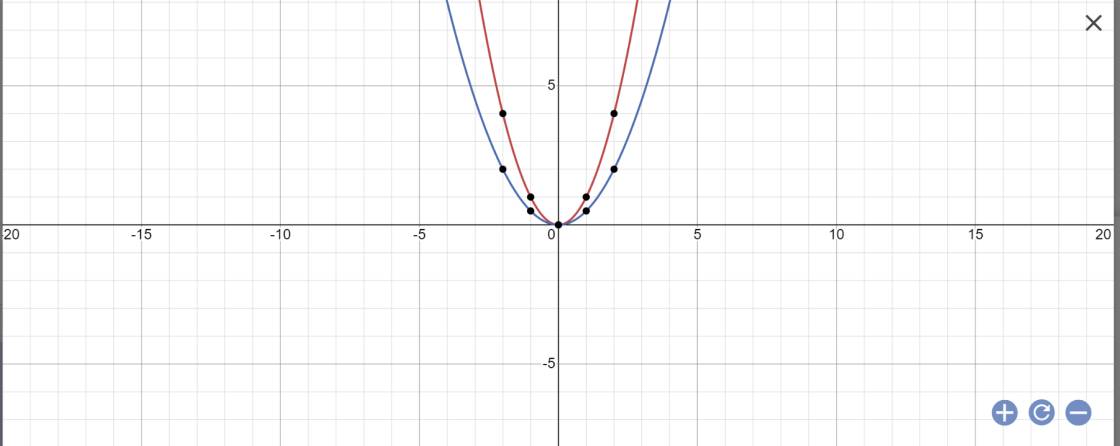 
b: Khi x=2 thì y=1/2*2^2=2
=>A(2;2)
Khi x=2 thì y=2^2=4
=>B(2;4)
c: Tọa độ A' là:
\(\left\{{}\begin{matrix}x_{A'}=-x_A=-2\\y_{A'}=y_A=2\end{matrix}\right.\)
Vì f(-2)=1/2*(-2)^2=2
nên A' thuộc (P1)
Tọa độ B' là:
\(\left\{{}\begin{matrix}x_{B'}=-x_B=-2\\y_{B'}=y_B=4\end{matrix}\right.\)
Vì f1(-2)=(-2)^2=4
nên B' thuộc y=x^2
Đúng 2
Bình luận (0)