1/ Cho \(\left|\overrightarrow{u}\right|=\sqrt{2}\) , \(\left|\overrightarrow{v}\right|=10\) , \(\overrightarrow{u}.\overrightarrow{v}=10\). Tính số đó góc hợp giữa \(\overrightarrow{u}và\overrightarrow{v}\) .
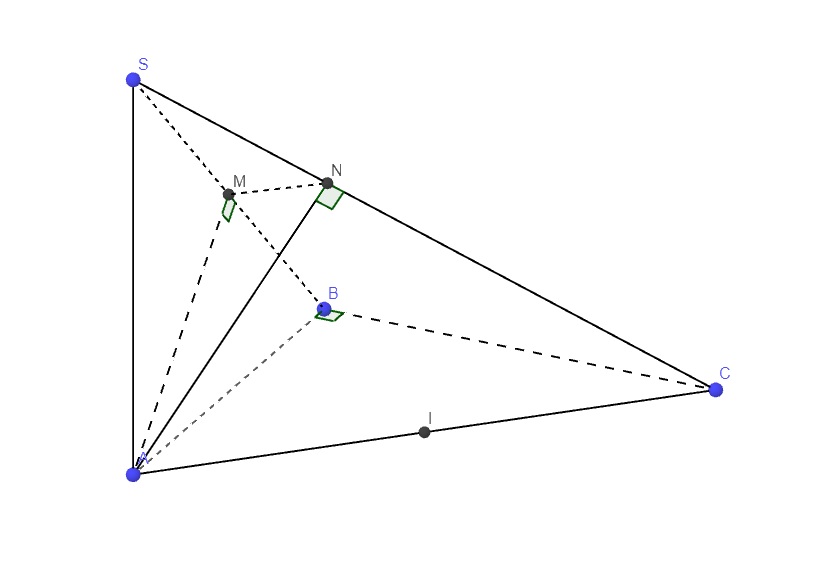
2/ Cho hình chóp S.ABC, đáy là tâm giác vuông cân tại B, SA vuông góc với mặt đáy, AB = SA = a
a. Tính góc 2mp ((SBC),(ABC))
b. Gọi M,N lần lượt là hình chiếu của A lên SB, SC. Tam giác AMN là tam giác gì? tính góc giữa 2mp ((AMN),(ABC)), góc giữa (AC;(AMN)).
c. Tính khoảng cách từ trung điểm I của đoạn thẳng AC đến mp (SBC)
3/ Cho hình chóp S.ABCD, đáy là hình vuống tâm O, SA = SB = SC = SD = AB = 2a. M,N lần lượt là trung điểm SB, SD.
a. Tính số đo của góc giữa (MN;SC)
b. SA vuống góc với đường thẳng nào?
c. Tính a khoảng cách giữa d(AB;(SCD)).
CỨU MK VS, MAI MK KT 15' mà mk lại ko lm đc, ko bt lm lun, giúp mk vs, cảm ơn nhiều.