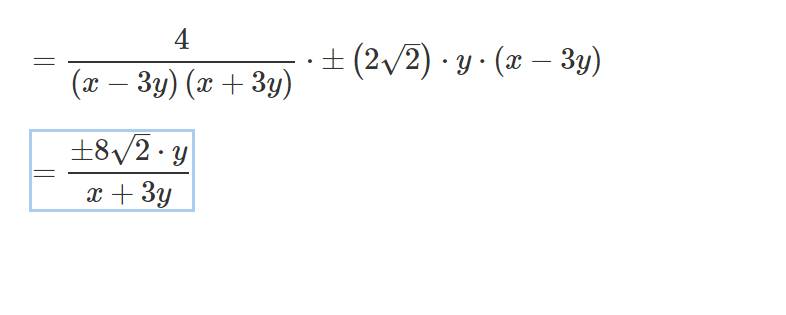c) (x+2)² - 9y²

Những câu hỏi liên quan
c/m dang thuc : (x^2 +3xy)/(x^2 - 9y^2) + (2x^2 -5xy-3y^2)/(x^2-6xy+9y^2)= (3x^2 +2xy+3xz +6yz)/(xz -3yz +z^2-3xy)
c/m dang thuc : (x^2 +3xy)/(x^2 - 9y^2) + (2x^2 -5xy-3y^2)/(x^2-6xy+9y^2)= (3x^2 +2xy+3xz +6yz)/(xz -3yz +z^2-3xy)
Phân tích đa thức thành nhân tử :
a) \(x^2-2x-9y^2-18y^2\)
b)\(x^2-4x-9y^2+4\)
c)\(x^2-2x-4x^2+1\)
d)\(4x^2-6x-9y^2+9y\)
\(b,x^2-4x-9y^2+4=\left(x-2\right)^2-\left(3y\right)^2=\left(x-2-3y\right)\left(x-2+3y\right)\)
\(c,x^2-2x-4x^2+1=\left(x-1\right)^2-\left(2x\right)^2=\left(x-1+2x\right)\left(x-2x-1\right)=\left(3x-1\right)\left(-x-1\right)\)
\(d,4x^2-6x-9y^2+9y=\left(4x^2-9y^2\right)-\left(6x-9y\right)=\left(2x-3y\right)\left(2x+3y\right)-3\left(2x-3y\right)=\left(2x+3y-3\right)\left(2x-3y\right)\)
Đúng 0
Bình luận (0)
(x + 9y / x^2 - 9y^2 - 3y / x^2 + 3xy) . x - 3xy / x + 3y
x mũ 2 y+ x mux2 - 9y mũ 2-9y
\(x^2y+x^2-9y^2-9y\)
\(=x^2\left(y+1\right)-9y\left(y+1\right)\)
\(=\left(y+1\right)\left(x^2-9y\right)\)
Đúng 1
Bình luận (2)
4/x^2 - 9y^2 nhân căn 8y^2(9y^2-6xy+x^2) cuu tuiiiiii
a) 4x2-9y2+6x-9y
b) 1-2x+2yz+x2-y2-z2
c) x3-1+5x2-5+3x-3
\(\frac{x+9y}{x^2-9y^2}-\frac{3y}{x^2+3xy}\)
đk: \(x\ne0\); \(x\ne\pm3y\)
\(\frac{x+9y}{x^2-9y^2}-\frac{3y}{x^2+3xy}\)
\(=\frac{x+9y}{\left(x-3y\right)\left(x+3y\right)}-\frac{3y}{x\left(x+3y\right)}\)
\(=\frac{x\left(x+9y\right)}{x\left(x-3y\right)\left(x+3y\right)}-\frac{3y\left(x-3y\right)}{x\left(x-3y\right)\left(x+3y\right)}\)
\(=\frac{x^2+9xy-3xy+9y^2}{x\left(x-3y\right)\left(x+3y\right)}\)
\(=\frac{\left(x+3y\right)^2}{x\left(x-3y\right)\left(x+3y\right)}\)
\(=\frac{x+3y}{x\left(x-3y\right)}\)
Đúng 0
Bình luận (0)
Phân tích đa thức thành nhân tử
a) x^2+2x+1-16y^2
b) x^2+6x-y^2+9
c) 4x^2+4x-9y^2+1
d) x^2-6xy+9y^2-25z^2
\(a=\left(x+1\right)^2-\left(4y\right)^2=\left(x+1-4y\right)\left(x+1+4y\right)\)
\(b=\left(x+3\right)^2-y^2=\left(x+3+y\right)\left(x+3-y\right)\)
\(c=\left(2x+1\right)^2-\left(3y\right)^2=\left(2x+1-3y\right)\left(2x+1+3y\right)\)
\(d=\left(x+3y\right)^2-\left(5z\right)^2=\left(x+3y-5z\right)\left(x+3y+5z\right)\)