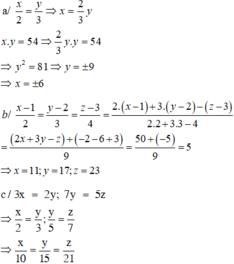a: \(=3x^4+3x^2y^2+2x^2y^2+2y^4+y^2\)

\(=\left(x^2+y^2\right)\left(3x^2+2y^2\right)+y^2\)

\(=3x^2+3y^2=3\)

b: \(=7\left(x-y\right)+4a\left(x-y\right)-5=-5\)

c: \(=\left(x-y\right)\left(x^2+xy+y^2\right)+xy\left(y-x\right)+3=3\)

d: \(=\left(x+y\right)^2-4\left(x+y\right)+1\)

=9-12+1

=-2

`#3107.101107`

`D = x^3 - y^3 - 3xy` biết `x - y - 1 = 0`

Ta có:

`x - y - 1 = 0`

`=> x - y = 1`

`D = x^3 - y^3 - 3xy`

`= (x - y)(x^2 + xy + y^2) - 3xy`

`= 1 * (x^2 + xy + y^2) - 3xy`

`= x^2+ xy + y^2 - 3xy`

`= x^2 - 2xy + y^2`

`= x^2 - 2*x*y + y^2`

`= (x - y)^2`

`= 1^2 = 1`

Vậy, với `x - y = 1` thì `D = 1`

________

`E = x^3 + y^3` với `x + y = 5; x^2 + y^2 = 17`

`x + y = 5`

`=> (x + y)^2 = 25`

`=> x^2 + 2xy + y^2 = 25`

`=> 2xy = 25 - (x^2 + y^2)`

`=> 2xy = 25 - 17`

`=> 2xy = 8`

`=> xy = 4`

Ta có:

`E = x^3 + y^3`

`= (x + y)(x^2 - xy + y^2)`

`= 5 * [ (x^2 + y^2) - xy]`

`= 5 * (17 - 4)`

`= 5 * 13`

`= 65`

Vậy, với `x + y = 5; x^2 + y^2 = 17` thì `E = 65`

________

`F = x^3 - y^3` với `x - y = 4; x^2 + y^2 = 26`

Ta có:

`x - y = 4`

`=> (x - y)^2 = 16`

`=> x^2 - 2xy + y^2 = 16`

`=> (x^2 + y^2) - 2xy = 16`

`=> 2xy = (x^2 + y^2) - 16`

`=> 2xy = 26 - 16`

`=> 2xy = 10`

`=> xy = 5`

Ta có:

`F = x^3 - y^3`

`= (x - y)(x^2 + xy + y^2)`

`= 4 * [ (x^2 + y^2) + xy]`

`= 4 * (26 + 5)`

`= 4*31`

`= 124`

Vậy, với `x - y = 4; x^2 + y^2 = 26` thì `F = 124.`

Sửa đề: Tìm x,y nguyên biết

Ta có: \(x^3y=xy^3+1997\)

=>\(x^3y-xy^3=1997\)

=>\(xy\left(x^2-y^2\right)=1997\)

=>xy(x-y)(x+y)=1997

Đặt A=xy(x-y)(x+y)

TH1: x chẵn; y chẵn

=>xy chẵn

=>xy(x-y)(x+y)⋮2

=>A⋮2(1)

TH2: x chẵn, y lẻ

=>xy chẵn

=>xy(x-y)(x+y)⋮2

=>A⋮2(2)

TH3: x lẻ; y chẵn

=>xy chẵn

=>A=xy(x-y)(x+y)⋮2(3)

TH4: x lẻ; y lẻ

=>x+y chẵn

=>(x+y)(x-y)xy⋮2

=>A⋮2(4)

Từ (1),(2),(3),(4) suy ra A⋮2

mà A=1997

và 1997 không chia hết cho 2

nên (x;y)∈∅

a) A = -1;                        b) B = ( x   +   y ) 3  =1.

@ Nguyễn Thị Thương Hoài

Giúp em với ạ.

Tìm \(x\); y nguyên hay thế nào em 

nguyên ạ

Ta có: \(\frac{3x-2y}{4}=\frac{2z-4x}{3}=\frac{4y-3z}{2}\)

=>\(\frac{12x-8y}{16}=\frac{6z-12x}{9}=\frac{8y-6z}{4}\)

Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:

\(\frac{12x-8y}{16}=\frac{6z-12x}{9}=\frac{8y-6z}{4}=\frac{12x-8y+6z-12x+8y-6z}{16+9+4}=0\)

=>12x=8y=6z

=>6x=4y=3z

=>\(\frac{6x}{12}=\frac{4y}{12}=\frac{3z}{12}\)

=>\(\frac{x}{2}=\frac{y}{3}=\frac{z}{4}\)

Đặt \(\frac{x}{2}=\frac{y}{3}=\frac{z}{4}=k\)

=>x=2k; y=3k; z=4k

\(x^3+y^3+z^3=2673\)

=>\(\left(2k\right)^3+\left(3k\right)^3+\left(4k\right)^3=2673\)

=>\(8k^3+27k^3+64k^3=2673\)

=>\(99k^3=2673\)

=>\(k^3=27=3^3\)

=>k=3

=>\(\begin{cases}x=2\cdot3=6\\ y=3\cdot3=9\\ z=4\cdot3=12\end{cases}\)

Tìm x phải có 2 vế chứ ~ đề thiếu trầm trọng ~

= nha bn