Giải phương trình x3 -12x - 16 =0

Những câu hỏi liên quan
Giải phương trình x3 -12x - 16 =0
\(x^3-12x-16=0\Leftrightarrow x^2\left(x+2\right)-2x\left(x+2\right)-8\left(x+2\right)=0\)
\(\Leftrightarrow\left(x+2\right)\left(x^2-2x-8\right)=0\)
\(\Leftrightarrow\left(x+2\right)\left[x\left(x-4\right)+2\left(x-4\right)\right]=0\)
\(\Leftrightarrow\left(x+2\right)^2\left(x-4\right)=0\Leftrightarrow\orbr{\begin{cases}x=-2\\x=4\end{cases}}\)
Đúng 0
Bình luận (0)
Giải phương trình:
(x+2)3-16.(x+2)=0
2x3-6x2+12x-8=0
\(\left(x+2\right)^3-16\left(x+2\right)=0\)
\(\Rightarrow\left(x+2\right)\left[\left(x+2\right)^2-16\right]=0\)
\(\Rightarrow\left(x+2\right)\left(x+2-4\right)\left(x+2+4\right)=0\)
\(\Rightarrow\left(x+2\right)\left(x-2\right)\left(x+6\right)=0\)
\(\Rightarrow\left[{}\begin{matrix}x+2=0\\x-2=0\\x+6=0\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}x=-2\\x=2\\x=-6\end{matrix}\right.\)
Vậy \(S=\left\{-2;2;-6\right\}\)
\(2x^3-6x^2+12x-8=0\)
\(\Rightarrow2x^3-2x^23+3.2^2-2^3=0\)
\(\Rightarrow\left(x-2\right)^3=0\)
\(\Rightarrow x-2=0\)
\(\Rightarrow x=2\)
Đúng 1
Bình luận (0)
Giải phương trình: x^4 + 5x^3 + 12x^2 + 20x + 16 =0?
Ai nhanh mk t.i.c.k
x⁴ + 5x³ + 12x² + 20x + 16 = 0
Nhận xét: vì 16/1 = (20/5)² ⇒ đây là pt đối xứng. Vì x = 0 không là nghiệm của pt nên chia 2 vế của pt cho x²⇒pt trở thành:
⇔x² + 5x + 12+ 20/x + 16/x² = 0
⇔(x²+ 16/x²) +5(x+4/x) + 12 = 0
đặt x+4/x = t ⇒ t² = x²+ 8 + 16/x²
học tốt!
Đúng 0
Bình luận (0)
- tiếp
⇒ t² -8 + 5t + 12 = 0
⇔ t² + 5t + 4 = 0
┌t = -1 ⇒ x+4/x = -1 ⇔x²+x + 4 = 0 ( phương trình vô nghiệm)
└t=-4 ⇒ x+4/x = -4 ⇔ x²+ 4x + 4 = 0 ⇔ x =-2
Vậy phương trình có 1 nghiệm duy nhất x=-2
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
Giá trị m để phương trình
x
3
−
12
x
+
m
−
2
0
có 3 nghiệm phân biệt. A.
−
4
m
4
B.
−
14
m
18
C.
−
18
m
14
D.
−
16
m
16...
Đọc tiếp
Giá trị m để phương trình x 3 − 12 x + m − 2 = 0 có 3 nghiệm phân biệt.
A. − 4 < m < 4
B. − 14 < m < 18
C. − 18 < m < 14
D. − 16 < m < 16
Đáp án B
Ta có: x 3 − 12 x + m − 2 = 0 ⇔ x 3 − 12 x − 2 = − m . Vẽ đồ thị hàm số y = x 3 − 12 x − 2 .
Để phương trình ban đầu có 3 nghiệm phân biệt thì đường thẳng y = − m giao với đồ thị hàm số y = x 3 − 12 x − 2 tại 3 điểm phân biệt ⇔ − 18 < − m < 14 ⇔ − 14 < m < 18.
Đúng 0
Bình luận (0)
Phương trình
x
3
-
12
x
+
m
-
2
0
có ba nghiệm phân biệt với m thuộc khoảng A.
-
18 m 14 B.
-
4 m 4 C.
-
14 m 18 D.
-
16 m 16
Đọc tiếp
Phương trình x 3 - 12 x + m - 2 = 0 có ba nghiệm phân biệt với m thuộc khoảng
A. - 18 < m < 14
B. - 4 < m < 4
C. - 14 < m < 18
D. - 16 < m < 16
Đáp án A
Phương pháp: Sử dụng sự tương giao giữa hai đồ thị hàm số để đánh giá số nghiệm của phương trình.
Cách giải: ![]()
Số nghiệm của phương trình (*) bằng số giao điểm của đồ thị hàm số ![]() và đường thẳng
và đường thẳng ![]()
Xét ![]() có
có ![]()
Bảng biến thiên:
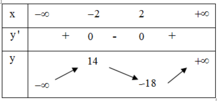
Khi đó, ![]() cắt
cắt ![]() tại 3 điểm phân biệt
tại 3 điểm phân biệt ![]()
Đúng 0
Bình luận (0)
Giải các phương trình:a)
3
x
−
3
4
−
2
−
4
x
0
;b)
x
2
−
4
x
+
7...
Đọc tiếp
Giải các phương trình:
a) 3 x − 3 4 − 2 − 4 x = 0 ;
b) x 2 − 4 x + 7 − 12 x + 7 = 0 ;
c) 4 − 4 + x + x x 2 − 16 = 0 ;
d) x 2 + 6 x − 7 = 0 .
Giải các phương trình sau: 2 x 3 + 2 x - 1 6 = 4 - x 3
2 x 3 + 2 x - 1 6 = 4 - x 3
⇔ 2.2x + 2x – 1 = 4.6 – 2x
⇔ 4x + 2x – 1 = 24 – 2x
⇔ 6x + 2x = 24 + 1
⇔ 8x = 25 ⇔ x = 25/8
Phương trình có nghiệm x = 25/8
Đúng 0
Bình luận (0)
Giải phương trình ;
(1+1/x3)(1+x)3=16
Tìm tất cả các giá trị thực của tham số m sao cho phương trình
x
3
−
12
x
+
m
−
2
0
có 3 nghiệm phân biệt. A.
−
16
m
16.
B.
−
18
m
14.
C.
−
14
m
...
Đọc tiếp
Tìm tất cả các giá trị thực của tham số m sao cho phương trình x 3 − 12 x + m − 2 = 0 có 3 nghiệm phân biệt.
A. − 16 < m < 16.
B. − 18 < m < 14.
C. − 14 < m < 18.
D. − 4 < m < 4.
Đáp án C
Phương trình ⇔ − m = x 3 − 12 x − 2 . Điều kiện trở thành đường y= m cắt đồ thị hàm số y = x 3 − 12 x − 2 tại 3 điểm phân biệt.
Lập bảng biến thiên của y = x 3 − 12 x − 2 .
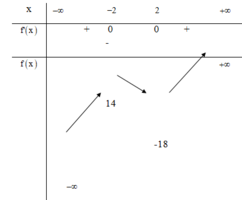
Nhìn vào bảng biến thiên, điều kiện của m là − m ∈ 14 ; − 18 ⇔ m ∈ − 14 ; 18 .
Đúng 0
Bình luận (0)
Gi ải các phương trình sau
e) x3-7x+6=0
f) x4-4x3+12x-9=0
g)x5-5x3+4x=0
h) x4-4x3+3x2+4x-4=0
a.
\(x^3-7x+6=0\)
\(\Leftrightarrow x^3-3x^2+2x+3x^2-9x+6=0\)
\(\Leftrightarrow x\left(x^2-3x+2\right)+3\left(x^2-3x+2\right)=0\)
\(\Leftrightarrow\left(x^2-3x+2\right)\left(x+3\right)=0\)
\(\Leftrightarrow\left(x^2-x-2x+2\right)\left(x+3\right)=0\)
\(\Leftrightarrow\left[x\left(x-1\right)-2\left(x-1\right)\right]\left(x+3\right)=0\)
\(\Leftrightarrow\left(x-1\right)\left(x-2\right)\left(x+3\right)=0\)
\(\Rightarrow\left[{}\begin{matrix}x=1\\x=2\\x=-3\end{matrix}\right.\)
Đúng 3
Bình luận (0)
f.
\(x^4-4x^3+12x-9=0\)
\(\Leftrightarrow x^4-4x^3+3x^2-3x^2+12x-9=0\)
\(\Leftrightarrow x^2\left(x^2-4x+3\right)-3\left(x^2-4x+3\right)=0\)
\(\Leftrightarrow\left(x^2-4x+3\right)\left(x^2-3\right)=0\)
\(\Leftrightarrow\left(x^2-x-3x+3\right)\left(x^2-3\right)=0\)
\(\Leftrightarrow\left[x\left(x-1\right)-3\left(x-1\right)\right]\left(x^2-3\right)=0\)
\(\Leftrightarrow\left(x-1\right)\left(x-3\right)\left(x^2-3\right)=0\)
\(\Rightarrow\left[{}\begin{matrix}x=1\\x=3\\x=\pm\sqrt{3}\end{matrix}\right.\)
Đúng 3
Bình luận (0)
g.
\(x^5-5x^3+4x=0\)
\(\Leftrightarrow x\left(x^4-5x^2+4\right)=0\)
\(\Leftrightarrow x\left(x^4-x^2-4x^2+4\right)=0\)
\(\Leftrightarrow x\left[x^2\left(x^2-1\right)-4\left(x^2-1\right)\right]=0\)
\(\Leftrightarrow x\left(x^2-1\right)\left(x^2-4\right)=0\)
\(\Leftrightarrow x\left(x-1\right)\left(x+1\right)\left(x-2\right)\left(x+2\right)=0\)
\(\Rightarrow\left[{}\begin{matrix}x=0\\x=\pm1\\x=\pm2\end{matrix}\right.\)
Đúng 2
Bình luận (0)
Xem thêm câu trả lời