Với hình vẽ bên hãy tính AB bằng 2 cách

Những câu hỏi liên quan
Câu 9. Nối mỗi đỉnh của hình vuông với trung điểm của cạnh đối diện như hình vẽ bên. Biết diện tích hình vuông bằng 2 200 . cm Hỏi diện tích phần tô đậm trong hình bằng kết quả nào sau đây?
A. 2 16 . cm B. 2 18 . cm C. 2 20 . cm D. 2 30 .
đưa hình đây trả lời cho
chưa có hình kìa bn
Đặt vật AB vuông góc với trục chính của thấu kính có tiêu cự 20 cm thì thu được ảnh thật cao bằng nửa vật.
a) Thấu kính đã cho là hội tụ hay phân kì? Vì sao?
b) Bằng phép vẽ, hãy xác định tiêu điểm F, F'? Nêu rõ cách vẽ.
c) Bằng kiến thức hình học, hãy xác định khoảng cách từ vật và ảnh đến thấu kính?
Cho hình vẽ bên:
a) hãy tính S hình tròn biết S hình vuông ABCD bằng 20 cm2
b) Tính S phần gạch chéo.
Đọc tiếp
Cho hình vẽ bên:
a) hãy tính S hình tròn biết S hình vuông ABCD bằng 20 cm2
b) Tính S phần gạch chéo.
câu 1 : cho đoạn thẳng AB3cm nằm song song với mặt gương phẳng và cách mặt gương 2cm: a, hãy vẽ ảnh AB của AB qua gương (ghi rõ cách vẽ ) b, tính độ lớn của ảnh và khoảng cách từ ảnh tới gương Bài 2: Chiếu tia tới SI lên 1 gương phẳng a, Vẽ tia phản xạ ( ghi rõ cách vẽ ) b,...
Đọc tiếp
câu 1 : cho đoạn thẳng AB=3cm nằm song song với mặt gương phẳng và cách mặt gương 2cm: a, hãy vẽ ảnh A'B' của AB qua gương (ghi rõ cách vẽ ) b, tính độ lớn của ảnh và khoảng cách từ ảnh tới gương Bài 2: Chiếu tia tới SI lên 1 gương phẳng a, Vẽ tia phản xạ ( ghi rõ cách vẽ ) b, Tính góc phản xạ biết góc tới bằng 20 độ
[Vật lí 7] Bài tập tết của mình nè | HOCMAI Forum - Cộng đồng học sinh Việt Nam
tham khảo ở đây nhé, Vương Kỳ Băng
Đúng 0
Bình luận (0)
Cho tam giác ABC có A =110 độ vẽ CM vuông góc với AB
a, Tính góc ACM
b, Bên ngoài tam giác vẽ 1 đường thẳng đi qua B tạo với BA 1 góc = góc ACM và cắt tia CM tại H . Chứng minh CA vuông góc với Bh
c, Tính góc BHM
nói cách làm và vẽ hình nữa nha
hãy vẽ hình theo cách diễn đạt bằng lời sau.Cho tam giác ABC .Vẽ AH vuông góc với BC(H thuộc BC)Từ H vẽ HM song song với AB(M thuộc AC)vẽ HN song song với AC (N thuộc AB).Nói ra cách vẽ
) Một vật sáng AB = 1 cm có dạng hình mũi tên được đặt vuông góc với trục chính của một thấu kính hội tụ, cách thấu kính 20 cm, A nằm trên trục chính. Thấu kính có tiêu cự 15 cm. a, Hãy vẽ ảnh của AB theo đúng tỉ lệ b, Nêu tính chất của ảnh c, Tính độ cao của ảnh
a)Bạn tự vẽ hình nha!!!
b)Ảnh thật, ngược chiều và lớn hơn vật.
c)Khoảng cách từ ảnh đến thấu kính:
\(\dfrac{1}{f}=\dfrac{1}{d}+\dfrac{1}{d'}\Rightarrow\dfrac{1}{15}=\dfrac{1}{20}+\dfrac{1}{d'}\)
\(\Rightarrow d'=60cm\)
Độ cao ảnh: \(\dfrac{h}{h'}=\dfrac{d}{d'}\)
\(\Rightarrow\dfrac{1}{h'}=\dfrac{20}{60}\Rightarrow h'=3cm\)
Đúng 1
Bình luận (0)
Một thấu kính hội tụ có tiêu cự 20 cm , một vật AB cho ảnh thật A' B' cao bằng nửa vật
a) Vẽ hình sự tạo ảnh
b) Dựa vào hình vẽ xác định vị trí của vật và ảnh so với thấu kính
c) Tính khoảng cách giữa vật và ảnh
Em đang cần gấp lắm ạ . Giải chi tiết giúp em với nha
Sơ đồ tạo ảnh:

Vật sáng AB là một đoạn thẳng đặt vuông góc trục chính của thấu kính cho ảnh cao gấp hai lần vật

Áp dụng công thức về vị trí ảnh – vật:
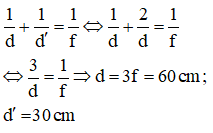
Đúng 1
Bình luận (1)
Bài 2: Cho hình vẽ bên. Biết rằng GF = 4cm, FH = 3cm, I là trung điểm GF, IK//FH. a) Tính GK. b) Cmr: KGF cân c) Cmr: KFH cân (bằng 2 cách) d) Hạ KM vuông góc với FH. Cmr: M là trung điểm FH(bằng 3 cách) e) Tính độ dài IM.

a) Ta có: \(GI=IF=\dfrac{GF}{2}\) ( do I là trung điểm GF)
\(\Rightarrow GI=GF=\dfrac{4}{2}=2\left(cm\right)\)
Xét ΔABC có:
I là trung điểm của GF(gt)
IK//FH(gt)
=> K là trung điểm của GH
=> IK là đường trung bình của tam giác ABC
=> \(IK=\dfrac{1}{2}FH=\dfrac{1}{2}.3=\dfrac{3}{2}\)(cm)
Xét tam giác GIK vuông tại I có:
\(GK^2=GI^2+IK^2\)( định lý Pytago)
\(\Rightarrow GK=\sqrt{GI^2+IK^2}=\sqrt{2^2+\left(\dfrac{3}{2}\right)^2}=\dfrac{5}{2}\left(cm\right)\)
b) Xét tam giác KGF có:
\(KI\perp GF\)( KI //FH, FH⊥GF=> KI⊥GF)
KI là đường trung tuyến( I là trung điểm của GF)
=> Tam giác KGF cân tại K
c) Cách 1:
Xét tam giác GCH vuông tại C có
FK là đường trung tuyến ứng với cạnh huyền GH( K là trung điểm của GH)
=> \(FK=\dfrac{1}{2}GH=KH\) \(\Rightarrow\Delta FKH\) cân tại K
Cách 2:
Xét tam giác GFH có:
IK là đường trung bình
=> IK//FH \(\Rightarrow\left\{{}\begin{matrix}\widehat{IKF}=\widehat{KFH}\\\widehat{GKI}=\widehat{KHF}\end{matrix}\right.\)
Mà \(\widehat{GKI}=\widehat{IKF}\) ( do tam giác GKF cân tại K nên KI là tia phân giác \(\widehat{GKF}\))
\(\Rightarrow\widehat{KFH}=\widehat{KHF}\Rightarrow\Delta KFH\) cân tại K
Đúng 0
Bình luận (0)
d) Cách 1:
Xét tam giác KFH cân tại K có:
KM là đường cao ( KM⊥FH)
=>KM là đường trung tuyến => M là trung điểm của FH
Cách 2:
Xét tứ giác IKMF có:
\(\widehat{KIF}=\widehat{IFM}=\widehat{FMK}=90^0\) => Tứ giác IKMF là hình chữ nhật
=> IK =FM mà \(FM=\dfrac{1}{2}FH\Rightarrow IK=\dfrac{1}{2}FH\Rightarrow M\) là trung điểm của FH
Cách 3:
Xét tam giác GFH có:
K là trung điểm của GH(IK là đường trung bình)
KM//GF( cùng vuông góc với FH)
=> M là trung điểm của FH
e) Xét tam giác GCH vuông tại C có:
\(GH^2=GC^2+CH^2\Rightarrow GH=\sqrt{GC^2+CH^2}=\sqrt{4^2+3^2}=5\left(cm\right)\)
Ta có: Tứ giác IKMF là hình chữ nhật
\(\Rightarrow IM=FK=\dfrac{1}{2}GH=\dfrac{1}{2}.5=\dfrac{5}{2}\left(cm\right)\)
Đúng 1
Bình luận (0)
Cho hình vẽ bên : a. Hãy tính diện tích hình tròn biết diện tích hình vuông ABCD bằng 20 cm vuông b.Tính diện tích phần còn lại.
Đọc tiếp
Cho hình vẽ bên : a. Hãy tính diện tích hình tròn biết diện tích hình vuông ABCD bằng 20 cm vuông b.Tính diện tích phần còn lại.
Ta thấy, cạnh của hình vuông gấp 2 lần bán kính của hình tròn
Gọi bán kính hình tròn là r
Theo bài ra ta có:
rx2xrx2=20(cm2)
=> rxr=20:4=5
=> Shình tròn =5x3,14=15,7(cm2)
=>S phần còn lại =20-15,7=4,3(cm2)
Đáp số: a) 15,7 cm2
b) 4,3 cm2
Đúng 1
Bình luận (2)






















