Phương trình hoành độ giao điểm của (P) và (d) là \(x^2=2x-m\Leftrightarrow x^2-2x+m=0\) (*)

Pt (*) có \(\Delta'=\left(-1\right)^2-1.m=1-m\)

Để (d) cắt (P) tại 2 điểm phân biệt \(x_1,x_2\) thì pt (*) phải có 2 nghiệm phân biệt \(x_1,x_2\) \(\Leftrightarrow\Delta'>0\Leftrightarrow1-m>0\Leftrightarrow m< 1\)

Khi \(m< 1\), áp dụng hệ thức Vi-ét, ta có \(\left\{{}\begin{matrix}x_1+x_2=2\\x_1x_2=m\end{matrix}\right.\)

Mà \(\left\{{}\begin{matrix}y_1=x_1^2\\y_2=x_2^2\end{matrix}\right.\)\(\Rightarrow y_1+y_2=x_1^2+x_2^2=\left(x_1+x_2\right)^2-2x_1x_2=2^2-2m=4-2m\)

Do đó để \(y_1+y_2+x_1^2x_2^2=6\left(x_1+x_2\right)\)\(\Leftrightarrow4-2m+m^2=6.2\)\(\Leftrightarrow m^2-2m-8=0\) (1)

pt (1) có \(\Delta'=\left(-1\right)^2-1.\left(-8\right)=9>0\)

Vậy (1) có 2 nghiệm phân biệt \(\left[{}\begin{matrix}m_1=\dfrac{-\left(-1\right)+\sqrt{9}}{1}=4\\m_2=\dfrac{-\left(-1\right)-\sqrt{9}}{1}=-2\end{matrix}\right.\)

Như vậy để (d) cắt (P) tại 2 điểm có hoành độ và tung độ thỏa mãn yêu cầu đề bài thì \(\left[{}\begin{matrix}m=4\\m=-2\end{matrix}\right.\)

Mà do \(m< 1\) nên ta chỉ nhận trường hợp \(m=-2\)

Vậy để (d) cắt (P) tại 2 điểm phân biệt có hoành độ và tung độ thỏa mãn đề bài thì \(m=-2\)

Phương trình hoành độ giao điểm của $\left(d\right)$ và $\left(P\right)$ là:

$x^2=2x-m\iff x^2-2x+m=0$ (1)

Ta có: ${\Delta }^{{}^{}}=1-m$.

Điều kiện để $\left(d\right)$ cắt $\left(P\right)$ tại hai điểm phân biệt là phương trình hoành độ giao điểm của $\left(d\right)$ và $\left(P\right)$ có hai nghiệm phân biệt.

Suy ra $1-m>0\iff m<1$ (*).

Khi đó $x_1$, $x_2$ là các hoành độ giao điểm của $\left(d\right)$ và $\left(P\right)$ nên $x_1$, $x_2$ là các nghiệm của phương trình hoành độ của $\left(d\right)$ và $\left(P\right)$.

Theo hệ thức Vi-et ta có: $\{\begin{array}{c}{x}_1+x_2=2\\ x_1{x}_2=m\end{array}$

Khi đó, $y_1+y_2+{x_1}^2{x_2}^2=6\left(x_1+x_2\right).$

$\iff {x_1}^2+{x_2}^2+{x_1}^2{x_2}^2=6\left(x_1+x_2\right).$

$\iff {\left(x_1+x_2\right)}^2-2x_1{x}_2+{x_1}^2{x_2}^2=6\left(x_1+x_2\right).$

$\iff 4-2m+m^2=12\iff m^2-2m-8=0\iff [\begin{array}{c}m=-2\left(\text{tm}(\ast )\right)\\ m=4\left(\text{ktm}(\ast )\right)\end{array}$

Vậy $m=-2$ là giá trị cần tìm.

Phương trình hoành độ giao điểm của $\left(d\right)$ và $\left(P\right)$ là:

$x^2=2x-m\iff x^2-2x+m=0$ (1)

Ta có: ${\Delta }^{{}^{}}=1-m$.

Điều kiện để $\left(d\right)$ cắt $\left(P\right)$ tại hai điểm phân biệt là phương trình hoành độ giao điểm của $\left(d\right)$ và $\left(P\right)$ có hai nghiệm phân biệt.

Suy ra $1-m>0\iff m<1$ (*).

Khi đó $x_1$, $x_2$ là các hoành độ giao điểm của $\left(d\right)$ và $\left(P\right)$ nên $x_1$, $x_2$ là các nghiệm của phương trình hoành độ của $\left(d\right)$ và $\left(P\right)$.

Theo hệ thức Vi-et ta có: $\{\begin{array}{c}{x}_1+x_2=2\\ x_1{x}_2=m\end{array}$

Khi đó, $y_1+y_2+{x_1}^2{x_2}^2=6\left(x_1+x_2\right).$

$\iff {x_1}^2+{x_2}^2+{x_1}^2{x_2}^2=6\left(x_1+x_2\right).$

$\iff {\left(x_1+x_2\right)}^2-2x_1{x}_2+{x_1}^2{x_2}^2=6\left(x_1+x_2\right).$

$\iff 4-2m+m^2=12\iff m^2-2m-8=0\iff [\begin{array}{c}m=-2\left(\text{tm}(\ast )\right)\\ m=4\left(\text{ktm}(\ast )\right)\end{array}$

Vậy $m=-2$ là giá trị cần tìm.

a: Để (d1) và (d2) cắt nhau thì \(2m+1\ne m+2\)

=>\(2m-m\ne2-1\)

=>\(m\ne1\)

b: Khi m=-1 thì (d1): \(y=\left(2-1\right)x+1=x+1\)

Khi m=-1 thì (d2): \(y=\left(1-2\right)x+2=-x+2\)

Vẽ đồ thị:

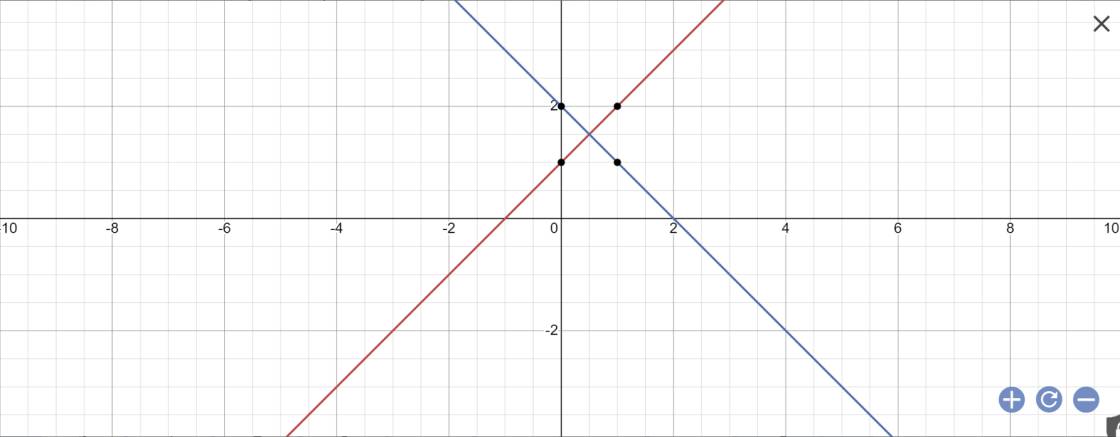
Phương trình hoành độ giao điểm là:

x+1=-x+2

=>x+x=2-1

=>2x=1

=>\(x=\dfrac{1}{2}\)

Thay x=1/2 vào y=x+1, ta được:

\(y=\dfrac{1}{2}+1=\dfrac{3}{2}\)

c:

(d1): y=(m+2)x+1

=>(m+2)x-y+1=0

Khoảng cách từ A(1;3) đến (d1) là:

\(d\left(A;\left(d1\right)\right)=\dfrac{\left|1\left(m+2\right)+3\cdot\left(-1\right)+1\right|}{\sqrt{\left(m+2\right)^2+\left(-1\right)^2}}\)

\(=\dfrac{\left|m\right|}{\sqrt{\left(m+2\right)^2+1}}\)

Để d(A;(d1)) lớn nhất thì m+2=0

=>m=-2

Vậy: \(d\left(A;\left(d1\right)\right)_{max}=\dfrac{\left|-2\right|}{\sqrt{\left(-2+2\right)^2+1}}=\dfrac{2}{1}=2\)

.

.

\(\dfrac{1}{2}x^2-\left(-2+1\right)x+\dfrac{-2-1}{2}=0\)

\(\Rightarrow\dfrac{1}{2}x^2+x-\dfrac{3}{2}=0\)

Tới đây dùng \(\Delta\) chứ, nếu bn lấy \(\dfrac{1}{2}\) đặt lm nhân tử chung thì ở đây hơi vô lí 

\(\Delta=b^2-4ac=1-4.\dfrac{1}{2}.\left(-\dfrac{3}{2}\right)=4>0\)

\(\Rightarrow\)Pt có 2 nghiệm phân biệt

\(\left\{{}\begin{matrix}x_1=\dfrac{-b+\sqrt{\Delta}}{2a}=\dfrac{-1+2}{1}=1\\x_2=\dfrac{-b-\sqrt{\Delta}}{2a}=\dfrac{-1-2}{1}=-3\end{matrix}\right.\)

Thay \(x_1=1\) vào \(y=\dfrac{1}{2}x^2\Rightarrow y=\dfrac{1}{2}\)

Thay \(x_2=-3\) vào \(y=-x+\dfrac{3}{2}\Rightarrow y=\dfrac{9}{2}\)

b: Phương trình hoành độ giao điểm là:

\(x^2-2\left(m-1\right)x-m^2-2m=0\)

\(\text{Δ}=\left[-2\left(m-1\right)\right]^2-4\left(-m^2-2m\right)\)

\(=4m^2-8m+4+4m^2+8m=8m^2+4>0\)

Vậy: Phương trình luôn có hai nghiệm phân biệt

\(x_1^2+x_2^2+4x_1x_2=36\)

\(\Leftrightarrow\left(x_1+x_2\right)^2+2x_1x_2=36\)

\(\Leftrightarrow\left[2\left(m-1\right)\right]^2+2\left(-m^2-2m\right)=36\)

\(\Leftrightarrow4m^2-8m+4-2m^2-4m-36=0\)

\(\Leftrightarrow2m^2-12m-32=0\)

\(\Leftrightarrow\left(m-8\right)\left(m+2\right)=0\)

hay \(m\in\left\{8;-2\right\}\)

Gọi \(A\left(x_1;x_1^2\right)\) và \(B\left(x_2;x_2^2\right)\) là 2 điểm thuộc (P) và đối xứng qua M

Do A; B đối xứng qua M

\(\Rightarrow\left\{{}\begin{matrix}x_1+x_2=2.\left(-1\right)\\x_1^2+x_2^2=2.5\end{matrix}\right.\)

\(\Rightarrow\left\{{}\begin{matrix}x_2=-2-x_1\\x_1^2+x_2^2=10\end{matrix}\right.\)

\(\Rightarrow x_1^2+\left(-2-x_1\right)^2=10\)

\(\Rightarrow2x_1^2+4x_1-6=0\Rightarrow\left[{}\begin{matrix}x_1=1\\x_1=-3\end{matrix}\right.\)

Vậy 2 điểm đó là \(\left(1;1\right)\) và \(\left(-3;9\right)\)

Phương trình hoành độ giao điểm là:

\(x^2-\left(2m+1\right)x+m^2-1=0\)

\(\text{Δ}=\left(2m+1\right)^2-4\left(m^2-1\right)\)

\(=4m^2+4m+1-4m^2+4=4m+5\)

Để (P) cắt (d) tại hai điểm nằm về hai phía của trục tung thì \(m^2-1< 0\)

hay -1<m<1

gợi ý nè .

1) áp dụng bunya

2)thử nhân Pt 2 với 5 rồi trừ đi thử

3) đặt x³=a,y²=b

=> a²+3a+1=b²

đến đây có thể xét delta hoặc...

a²<a²+3a+1<a²+4a+4

=> a²<b²<(a+2)²

x,y nguyên nên a,b nguyên => b²=(a+1)²<=> a²+3a+1=a²+2a+1

<=> a=0 => b=1 => x=0 ,y=1

câu 3:

đặt x³=a, y²=b.(a,b nguyên ) ta viết lại Pt a²+3a+1=b²

\(\Leftrightarrow4a^2+12a+4=4b^2\)

\(\Leftrightarrow\left(2a+3\right)^2-4b^2=5\)

\(\Leftrightarrow\left(2a-2b+3\right)\left(2a+2b+3\right)=5\)

vì a,b nguyên nên ta có bảng :

(2a-2b+3)(2a+2b+3)=5=1.5=5.1=(-1).(-5)=(-5).(-1)

.....

P/s: cách bên trên sẽ bị thiếu nghiệm , I can't explain it thế nào

Bạn tham khảo:

Câu hỏi của Thiếu Niên Thần Thánh - Toán lớp 9 | Học trực tuyến