Cho hai đường tròn (O; R) và (O' R') tiếp xúc ngoài tại A. Các điểm M và N lần lượt chạy trên các đường tròn (O; R) và (O' R') bắt đầu từ A cùng chiều kim đồng hồ sao cho số đo cung AM bằng số đo cung AN. Chứng minh 3 điểm M, A, N thẳng hàng

Những câu hỏi liên quan
cho hai đường tròn tâm O và O' tiếp xúc ngoài với nhau tại A, có đường kính AB của đường tròn tâm O, đường kính AC của đường tròn O', gọi MN là tiếp tuyến chung của hai đường tròn (M thuộc đường tròn O, N thuộc đường tròn O') hai tia BM và CN cắt nhau tại E. a) CM: tam giác EBC là tam giác vuông b) CM: EB.EM=EN.EC c) Tính MN biết bán kính của đường tròn (O) và (O') lần lượt là 9cm và 4cm
Cho đường tròn tâm O bán kính 2cm. Trên đường tròn (o) ta lấy điểm o' &vẽ đường tròn (o';2cm).hai đường tròn này cắt nhau tại hai điểm A,B.tính O,O'
Cho đường tròn (O) và điểm A nằm ngoài đường tròn (O). Từ A kẻ hai tiếp tuyến AB, AC với đường tròn (O) ( B và C là các tiếp điểm). Đường thẳng CO cắt đường tròn (O) tại điểm thứ hai là D) ; đường thẳng AD cắt đường tròn (O) tại điểm thứ hai là E .a) Chứng minh tứ giác ABOC nội tiếp đường tròn.b) Gọi H là giao điểm của A0 và BC . Chứng minh AE.AD AH.AO AB^2.c) Đường thẳng BE cắt AO tại F. Chứng minh HE vuông góc với BF.giúp tớ với ạ tớ đang cần luôn phần b và c. tớ cảm ơn nhiều ạ
Đọc tiếp
Cho đường tròn (O) và điểm A nằm ngoài đường tròn (O). Từ A kẻ hai tiếp tuyến AB, AC với đường tròn (O) ( B và C là các tiếp điểm). Đường thẳng CO cắt đường tròn (O) tại điểm thứ hai là D) ; đường thẳng AD cắt đường tròn (O) tại điểm thứ hai là E .
a) Chứng minh tứ giác ABOC nội tiếp đường tròn.
b) Gọi H là giao điểm của A0 và BC . Chứng minh AE.AD = AH.AO = AB^2.
c) Đường thẳng BE cắt AO tại F. Chứng minh HE vuông góc với BF.
giúp tớ với ạ tớ đang cần luôn phần b và c. tớ cảm ơn nhiều ạ
a: góc ABO+góc ACO=180 độ
=>ABOC nội tiếp
b: Xét (O) có
AB,AC là tiếp tuyến
=>AB=AC
mà OB=OC
nên OA là trung trực của BC
=>OA vuông góc BC tại H
=>AH*AO=AB^2
Xét ΔABE và ΔADB có
góc ABE=góc ADB
góc BAE chung
=>ΔABE đồng dạng với ΔADB
=>AB^2=AE*AD=AH*AO
Đúng 1
Bình luận (1)
Cho đường tròn (O) và điểm A nằm ngoài đường tròn (O). Từ A kẻ hai tiếp tuyến AB, AC với đường tròn (O). Đường thẳng CO cắt đường tròn (O) tại điểm thứ hai là D; đường thẳng AD cắt đường tròn (O) tại điểm thứ hai là E. BE cắt AO tại F,H là giao điểm của AO và BC a,CM ODEH nội tiếp đường tròn b,CM HE vuông góc với BF
Đọc tiếp
Cho đường tròn (O) và điểm A nằm ngoài đường tròn (O). Từ A kẻ hai tiếp tuyến AB, AC với đường tròn (O). Đường thẳng CO cắt đường tròn (O) tại điểm thứ hai là D; đường thẳng AD cắt đường tròn (O) tại điểm thứ hai là E. BE cắt AO tại F,H là giao điểm của AO và BC
a,CM ODEH nội tiếp đường tròn
b,CM HE vuông góc với BF
a,CM ODEH nội tiếp đường tròn
b,CM HE vuông góc với BF
a: Xét ΔABE và ΔADB co
góc ABE=góc ADB
góc BAE chung
=>ΔABE đồng dạng với ΔADB
=>AB/AD=AE/AB
=>AB^2=AD*AE
Xét (O) có
AB,AC là tiếp tuyến
=>AB=AC
mà OB=OC
nên OA là trung trực của BC
=>OA vuông góc BC tại H
=>AH*AO=AB^2=AE*AD
=>AH/AD=AE/AO
=>ΔAHE đồng dạng với ΔADO
=>góc AHE=góc ADO
=>góc OHE+góc ODE=180 độ
=>OHED nội tiếp
b: OHED nội tiếp
=>góc HED+góc HOD=180 độ
BD//AO
=>góc BDO+góc HOD=180 độ
=>góc BDO=góc HED
góc BCD+góc BDC=90 độ
góc BCD=góc BED
=>góc HED+góc BED=90 độ
=>HE vuông góc BF tại E
Đúng 1
Bình luận (0)
Cho hai đường tròn (O) và (O) có cùng bán kính R cắt nhau tại hai điểm A, B sao cho tâm O nằm trên đường tròn (O) và tâm O nằm trên đường tròn (O). Đường nối tâm OO cắt AB tại H, cắt đường tròn (O) tại giao điểm thứ hai là C. Gọi F là điểm đối xứng của B qua O.a) Chứng minh rằng AC là tiếp tuyến của (O), và AC vuông góc BF.b) Trên cạnh AC lấy điểm D sao cho AD AF. Qua D kẽ đường thăng vuông góc với OC cắt OC tại K, Cắt AF tại G. Gọi E là giao điểm của AC và BF. Chứng minh các tứ giác AHOE, ADKO...
Đọc tiếp
Cho hai đường tròn (O) và (O') có cùng bán kính R cắt nhau tại hai điểm A, B sao cho tâm O nằm trên đường tròn (O') và tâm O' nằm trên đường tròn (O). Đường nối tâm OO' cắt AB tại H, cắt đường tròn (O') tại giao điểm thứ hai là C. Gọi F là điểm đối xứng của B qua O'.
a) Chứng minh rằng AC là tiếp tuyến của (O), và AC vuông góc BF.
b) Trên cạnh AC lấy điểm D sao cho AD = AF. Qua D kẽ đường thăng vuông góc với OC cắt OC tại K, Cắt AF tại G. Gọi E là giao điểm của AC và BF. Chứng minh các tứ giác AHO'E, ADKO là các tứ giác nội tiếp.
c) Tứ giác AHKG là hình gì? Vì sao.
d) Tính diện tích phần chung của hình (O) và hình tròn (O') theo bán kính R.
Cho hai đường tròn (O; R) và (O'; r) tiếp xúc ngoài (R > r). Hai tiếp tuyến chung AB và A'B' của hai đường tròn (O),(O') cắt nhau tại P(A và A' thuộc đường tròn (O'), B và B' thuộc đường tròn (O)). Biết PA = AB = 4 cm. Tính diện tích hình tròn (O').

(O; R) và (O’; R’) tiếp xúc ngoài với nhau
⇒ OO’ = R + r.
O’A ⊥ BP, OB ⊥ BP ⇒ O’A // OB
⇒ ΔPAO’  ΔPBO
ΔPBO

⇒ OB = 2.O'A hay R = 2.r
và OP = 2.O’P ⇒ O’P = OO’ = R + r = 3.r
ΔO’AP vuông tại A nên:
O ’ P 2 = O ’ A 2 + A P 2
⇔ ( 3 r ) 2 = r 2 + 4 2 ⇔ 8 r 2 = 16 ⇔ r 2 = 2
Diện tích hình tròn (O’; r) là: S = π . r 2 = 2 π ( c m 2 ) .
Đúng 0
Bình luận (0)
Cho hai đường tròn (O; R) và (O'; r) tiếp xúc ngoài (R > r). Hai tiếp tuyến chung AB và A'B' của hai đường tròn (O),(O') cắt nhau tại P(A và A' thuộc đường tròn (O'), B và B' thuộc đường tròn (O)). Biết PA = AB = 4 cm. Tính diện tích hình tròn (O').

(O; R) và (O’; R’) tiếp xúc ngoài với nhau
⇒ OO’ = R + r.
O’A ⊥ BP, OB ⊥ BP ⇒ O’A // OB
⇒ ΔPAO’  ΔPBO
ΔPBO

⇒ OB = 2.O'A hay R = 2.r
và OP = 2.O’P ⇒ O’P = OO’ = R + r = 3.r
ΔO’AP vuông tại A nên: O ' P 2 = O ' A 2 + A P 2
⇔ ( 3 r ) 2 = r 2 + 4 2 ⇔ 8 r 2 = 16 ⇔ r 2 = 2
Diện tích hình tròn (O’; r) là: S = π · r 2 = 2 π cm 2
Đúng 0
Bình luận (0)
Cho hai đường tròn (O) và (O') tiếp xúc ngoài ở A . Đường nối tâm OO' cắt đường tròn (O) ở B , cắt đường tròn (O') ở C . DE là tiếp tuyến chung ngoài của hai đường tròn , D thuộc (O) và E thuộc (O') . Gọi M là giao điểm của hai đường thẳng BD và CE . Chứng minh :
a) MA là tiếp tuyến chung của hai đường tròn (O) và (O')
b) MD.MB=ME.MC
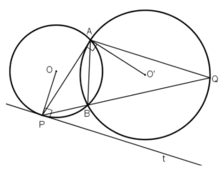
Cho hai đường tròn (O) và (O') cắt nhau tại A và B. Tiếp tuyến tại A của đường tròn (O') cắt đường tròn (O) tại điểm thứ hai P. Tia PB cắt đường tròn (O') tại Q. Chứng minh đường thẳng AQ song song với tiếp tuyến tại P của đường tròn (O).
Cho hai đường tròn (O) và (O') cắt nhau tại A và B. Tiếp tuyến tại A của đường tròn (O') cắt đường tròn (O) tại điểm thứ hai P. Tia PB cắt đường tròn (O') tại Q. Chứng minh đường thẳng AQ song song với tiếp tuyến tại P của đường tròn (O).
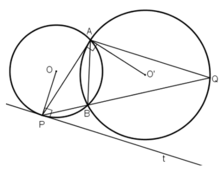


Kiến thức áp dụng
Trong một đường tròn:
+ Số đo của góc nội tiếp bằng một nửa số đo của cung bị chắn.
+ Số đo của góc tạo bởi tiếp tuyến và dây cung bằng nửa số đo của cung bị chắn.
Đúng 0
Bình luận (0)