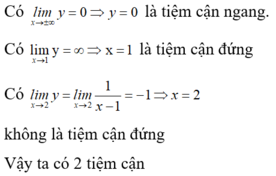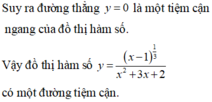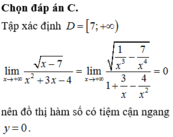Đồ thị hàm số `y = (x - sqrt{x^2 + 3x - 6})/(x^2 - 4)` có bao nhiêu đường tiệm cận

Những câu hỏi liên quan
Đồ thị hàm số
y
x
−
2
x
2
−
3
x
+
2
có bao nhiêu đường tiệm cận? A. 4 B. 1 C. 3 D. 2
Đọc tiếp
Đồ thị hàm số y = x − 2 x 2 − 3 x + 2 có bao nhiêu đường tiệm cận?
A. 4
B. 1
C. 3
D. 2
Đồ thị hàm số
y
x
-
1
1
3
x
2
+
3
x
+
2
có bao nhiêu đường tiệm cận? A. 1. B. 4. C. 3. D. 2.
Đọc tiếp
Đồ thị hàm số y = x - 1 1 3 x 2 + 3 x + 2 có bao nhiêu đường tiệm cận?
A. 1.
B. 4.
C. 3.
D. 2.
Đồ thị hàm số
y
x
−
2
x
2
−
3
x
+
2
có bao nhiêu đường tiệm cận? A. 4 B. 1 C. 3 D. 2
Đọc tiếp
Đồ thị hàm số y = x − 2 x 2 − 3 x + 2 có bao nhiêu đường tiệm cận?
A. 4
B. 1
C. 3
D. 2
Đáp án D
Có l i m x → ± ∞ y = 0 ⇒ y = 0 là tiệm cận ngang.
Có lim x → 1 y = ∞ ⇒ x = 1 là tiệm cận đứng
Có l i m x → 2 y = l i m x → 2 1 x − 1 = − 1 ⇒ x = 2 không là tiệm cận đứng
Vậy ta có 2 tiệm cận
Đúng 0
Bình luận (0)
Đồ thị hàm số y = x - 7 x 2 + 3 x - 4 có bao nhiêu đường tiệm cận?
A. 0
B. 3
C. 1
D. 2
Đồ thị hàm số y = x - 7 x 2 + 3 x - 4 có bao nhiêu đường tiệm cận?
A. 0
B. 3
C. 1
D. 2
26. Tìm số đường tiệm cận ngang và số đường tiệm cận đứng của đồ thị hàm số y = \(\dfrac{\sqrt{x-1}}{x^2-3x+2}\)
\(\lim\limits_{x\rightarrow+\infty}\dfrac{\sqrt{x-1}}{x^2-3x+2}=\lim\limits_{x\rightarrow+\infty}\dfrac{\sqrt{\dfrac{1}{x^3}-\dfrac{1}{x^4}}}{1-\dfrac{3}{x}+\dfrac{2}{x^2}}=0\)
\(\Rightarrow y=0\) là tiệm cận ngang
\(\lim\limits_{x\rightarrow1^+}\dfrac{\sqrt{x-1}}{x^2-3x+2}=\lim\limits_{x\rightarrow1^+}\dfrac{1}{\sqrt{x-1}\left(x-2\right)}=\infty\)
\(\Rightarrow x=1\) là tiệm cận đứng
\(\lim\limits_{x\rightarrow2}\dfrac{\sqrt{x-1}}{x^2-3x+2}=\dfrac{1}{0}=\infty\)
\(\Rightarrow x=2\) là tiệm cận đứng
ĐTHS có 1 TCN và 2 TCĐ
Đúng 1
Bình luận (0)
Hỏi đồ thị hàm số y = x − 1 x 2 − 3 x + 2 có đúng bao nhiêu tiệm cận đứng và tiệm cận ngang?
A. 3
B. 0
C. 2
D. 1
Phương pháp:
+) Đường thẳng x = a được gọi là TCĐ của đồ thị hàm số


Chọn: A
Đúng 0
Bình luận (0)
Đồ thị hàm số
y
x
-
1
x
3
-
3
x
có bao nhiêu đường tiệm cận đứng? A. 1. B. 2. C. 4. D. 3.
Đọc tiếp
Đồ thị hàm số y = x - 1 x 3 - 3 x có bao nhiêu đường tiệm cận đứng?
A. 1.
B. 2.
C. 4.
D. 3.
Đồ thị hàm số
y
x
-
1
x
2
-
3
x
+
2
có bao nhiêu tiệm cận?
Đọc tiếp
Đồ thị hàm số y = x - 1 x 2 - 3 x + 2 có bao nhiêu tiệm cận?
![]()
![]()
![]()
![]()