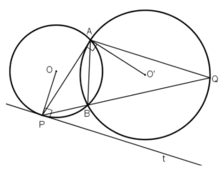
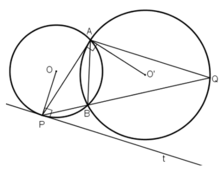
Cho hai đường tròn (O;R) và (O' ;R') cắt nhau tại 2 điểm phân biệt A và B. Từ một điểm C thay đổi trên tia đối của tia AB. Vẽ các tiếp tuyến CD, CE với đường tròn (O) (D,E là các tiếp điểm và E nằm trong đường tròn (O')).Hai đường thẳng AD và AE cắt (O') lần lượt tại M và N (M,N khác với điểm A). Đường thẳng DE cắt MN tại I. Chứng minh rằng:
a, MI.BE=BI.AE
b, Khi điểm C thay đổi thì đường DE luôn đi qua một điểm cố định













 ΔPBO
ΔPBO

 ΔPBO
ΔPBO