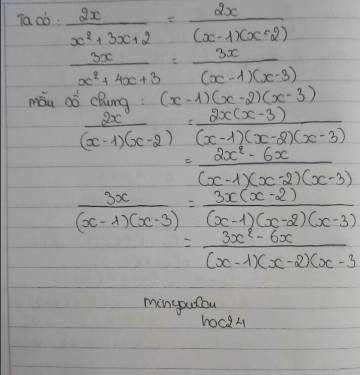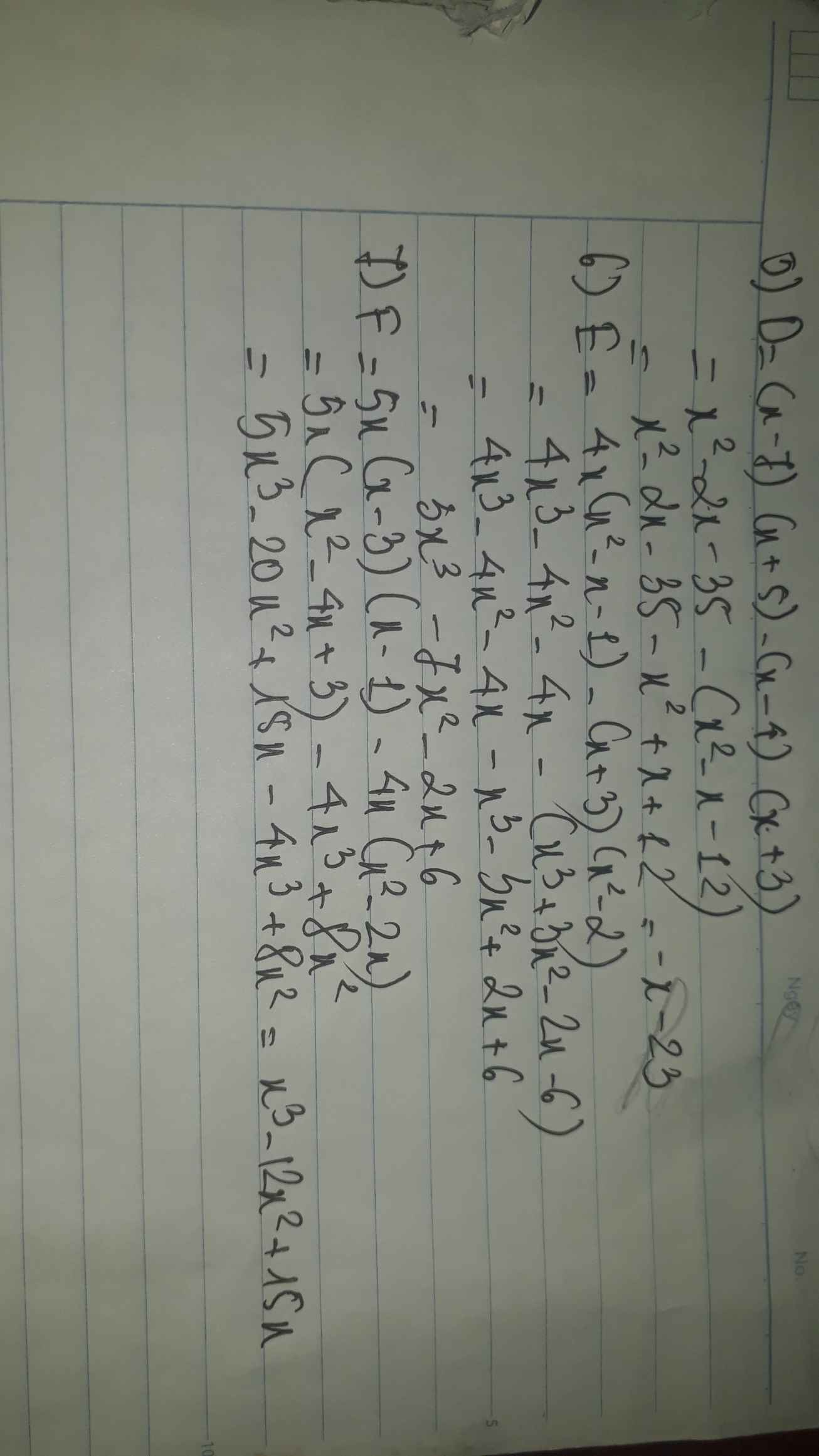A = - 3\(x\).(\(x-5\)) + 3(\(x^2\) - 4\(x\)) - 3\(x\) - 10

A = - 3\(x^2\) + 15\(x\) + 3\(x^2\) - 12\(x\) - 3\(x\) - 10

A = (- 3\(x^2\) + 3\(x^2\)) + (15\(x\) - 12\(x\) - 3\(x\)) - 10

A = 0 + (3\(x-3x\)) - 10

A = 0  - 10

A = - 10 

1) \(\left(\dfrac{1}{2}x+3\right)\left(x^2-4x-6\right)\)

\(=\dfrac{1}{2}x^3-2x^2-3x+3x^2-12x-18\)

\(=\dfrac{1}{2}x^3+x^2-15x-18\)

2) \(\left(6x^2-9x+15\right)\left(\dfrac{2}{3}x+1\right)\)

\(=4x^3+6x^2-6x^2-9x+10x+15\)

\(=4x^3+x+15\)

3) Ta có: \(\left(3x^2-x+5\right)\left(x^3+5x-1\right)\)

\(=3x^5+15x^2-3x^2-x^4-5x^2+x+5x^3+25x-5\)

\(=3x^5-x^4+5x^3+10x^2+26x-5\)

4) Ta có: \(\left(x-1\right)\left(x+1\right)\left(x-2\right)\)

\(=\left(x^2-1\right)\left(x-2\right)\)

\(=x^3-2x^2-x+2\)

lớp 8 có pt bậc 2 ak??

\(m,x^2+6x-16=0\)

\(\Leftrightarrow x^2-2x+8x-16=0\)

\(\Leftrightarrow x\left(x-2\right)+8\left(x-2\right)=0\)

\(\Leftrightarrow\left(x+8\right)\left(x-2\right)=0\)

\(\Leftrightarrow\left[{}\begin{matrix}x+8=0\\x-2=0\end{matrix}\right.\)

\(\Leftrightarrow\left[{}\begin{matrix}x=-8\\x=2\end{matrix}\right.\)

\(n,2x^2+5x-3=0\)

\(\Leftrightarrow2x^2-x+6x-3=0\)

\(\Leftrightarrow x\left(2x-1\right)+3\left(2x-1\right)=0\)

\(\Leftrightarrow\left(x+3\right)\left(2x-1\right)=0\)

\(\Leftrightarrow\left[{}\begin{matrix}x+3=0\\2x-1=0\end{matrix}\right.\)

\(\Leftrightarrow\left[{}\begin{matrix}x=-3\\x=\dfrac{1}{2}\end{matrix}\right.\)

\(k,x\left(2x-7\right)-4x+14=0\)

\(\Leftrightarrow2x^2-4x-7x+14=0\)

\(\Leftrightarrow2x\left(x-2\right)-7\left(x-2\right)=0\)

\(\Leftrightarrow\left(2x-7\right)\left(x-2\right)=0\)

\(\Leftrightarrow\left[{}\begin{matrix}2x-7=0\\x-2=0\end{matrix}\right.\)

\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{7}{2}\\x=2\end{matrix}\right.\)

\(a,\Rightarrow\left(2x-5\right)^2+2\left(2x-5\right)\left(x+2\right)+\left(x+2\right)^2=0\\ \Rightarrow\left(2x-5+x+2\right)^2=0\\ \Rightarrow3x-3=0\\ \Rightarrow x=1\\ b,\Rightarrow9-\left(x^2-5x\right)^2=9\\ \Rightarrow x^2-5x=0\\ \Rightarrow x\left(x-5\right)=0\Rightarrow\left[{}\begin{matrix}x=0\\x=5\end{matrix}\right.\)

1)(x²-4x+16)(x+4)-x(x+1)(x+2)+3x²=0

\(\Rightarrow\)(x³+64)-x(x²+2x+x+2)+3x²=0

\(\Rightarrow\)x³+64-x³-2x²-x²-2x+3x²=0

\(\Rightarrow\)-2x+64=0

\(\Rightarrow\)-2x=-64

\(\Rightarrow\)x=\(\dfrac{-64}{-2}\)

\(\Rightarrow x=32\)

2)(8x+2)(1-3x)+(6x-1)(4x-10)=-50

\(\Rightarrow\)8x-24x²+2-6x+24x²-60x-4x+10=50

\(\Rightarrow\)-62x+12=50

\(\Rightarrow\)-62x=50-12

\(\Rightarrow\)-62x=38

\(\Rightarrow\)x=\(-\dfrac{38}{62}=-\dfrac{19}{31}\)

3)(x²+2x+4)(2-x)+x(x-3)(x+4)-x²+24=0

\(\Rightarrow\)8-x³+x(x²+4x-3x-12)-x²+24=0

\(\Rightarrow\)8-x³+x³+4x²-3x²-12x-x²+21=0

\(\Rightarrow\)-12x+29=0

\(\Rightarrow\)-12x=-29

\(\Rightarrow\)x=\(\dfrac{-29}{-12}=\dfrac{29}{12}\)

a) x³y + x - y - 1

= (x³y - y) + (x - 1)

= y(x³ - 1) + (x - 1)

= y(x - 1)(x² + x + 1) + (x - 1)

= (x - 1)[y(x² + x + 1) + 1]

= (x - 1)(x²y + xy + y + 1)

b) x²(x - 2) + 4(2 - x)

= x²(x - 2) - 4(x - 2)

= (x - 2)(x² - 4)

= (x - 2)(x - 2)(x + 2)

= (x - 2)²(x + 2)

c) x³ - x² - 20x

= x(x² - x - 20)

= x(x² + 4x - 5x - 20)

= x[(x² + 4x) - (5x + 20)]

= x[x(x + 4) - 5(x + 4)]

= x(x + 4)(x - 5)

d) (x² + 1)² - (x + 1)²

= (x² + 1 - x - 1)(x² + 1 + x + 1)

= (x² - x)(x² + x + 2)

= x(x - 1)(x² + x + 2)

e) 6x² - 7x + 2

= 6x² - 3x - 4x + 2

= (6x² - 3x) - (4x - 2)

= 3x(2x - 1) - 2(2x - 1)

= (2x - 1)(3x - 2)

f) x⁴ + 8x² + 12

= x⁴ + 2x² + 6x² + 12

= (x⁴ + 2x²) + (6x² + 12)

= x²(x² + 2) + 6(x² + 2)

= (x² + 2)(x² + 6)

g) (x³ + x + 1)(x³ + x) - 2

Đặt u = x³ + x

x³ + x + 1 = u + 1

(u + 1).u - 2

= u² + u - 2

= u² - u + 2u - 2

= (u² - u) + (2u - 2)

= u(u - 1) + 2(u - 1)

= (u - 1)(u + 2)

= (x³ + x - 1)(x³ + x + 2)

= (x³ + x - 1)(x³ + x² - x² - x + 2x + 2)

= (x³ + x - 1)[(x³ + x²) - (x² + x) + (2x + 2)]

= (x³ + x - 1)[x²(x + 1) - x(x + 1) + 2(x + 1)]

= (x³ + x - 1)(x - 1)(x² - x + 2)

h) (x + 1)(x + 2)(x + 3)(x + 4) - 1

= [(x + 1)(x + 4)][(x + 2)(x + 3)] - 1

= (x² + 5x + 4)(x² + 5x + 6) - 1 (1)

Đặt u = x² + 5x + 4

u + 2 = x² + 5x + 6

(1) u.(u + 2) - 1

= u² + 2u - 1

= u² + 2u + 1 - 2

= (u² + 2u + 1) - 2

= (u + 1)² - 2

= (u + 1 + √2)(u + 1 - √2)

= (x² + 5x + 4 + 1 + √2)(x² + 5x + 4 + 1 - √2)

= (x² + 5x + 5 + √2)(x² + 5x + 5 - √2)

i: \(-\left(x^2+2\right)^2+4x\left(x^2+2\right)-3x^2\)

\(=-\left[\left(x^2+2\right)^2-4x\left(x^2+2\right)+3x^2\right]\)

\(=-\left[\left(x^2+2\right)^2-x\left(x^2+2\right)-3x\left(x^2+2\right)+3x^2\right]\)

\(=-\left[\left(x^2+2\right)\left(x^2+2-x\right)-3x\left(x^2+2-x\right)\right]\)

\(=-\left(x^2+2-x\right)\left(x^2-3x+2\right)\)

\(=-\left(x+2\right)\left(x-1\right)\left(x-2\right)\left(x-1\right)\)

\(=-\left(x+2\right)\left(x-2\right)\left(x-1\right)^2\)

l: \(81x^4+4y^4\)

\(=81x^4+36x^2y^2+4y^4-36x^2y^2\)

\(=\left(81x^4+36x^2y^2+4y^4\right)-\left(6xy\right)^2\)

\(=\left[\left(9x^2\right)^2+2\cdot9x^2\cdot2y^2+\left(2y^2\right)^2\right]-\left(6xy\right)^2\)

\(=\left(9x^2+2y^2\right)^2-\left(6xy\right)^2\)

\(=\left(9x^2+2y^2+6xy\right)\left(9x^2+2y^2-6xy\right)\)

\(a,\Rightarrow4x^2-20x-4x^2+3x+4x-3=5\\ \Rightarrow-13x=8\Rightarrow x=-\dfrac{8}{13}\\ b,\Rightarrow3x^2-10x+8-3x^2+27x=-3\\ \Rightarrow17x=-11\Rightarrow x=-\dfrac{11}{17}\\ c,\Rightarrow\left(x+3\right)\left(2-x\right)=0\Rightarrow\left[{}\begin{matrix}x=-3\\x=2\end{matrix}\right.\\ d,\Rightarrow2x\left(4x^2-25\right)=0\\ \Rightarrow2x\left(2x-5\right)\left(2x+5\right)=0\Rightarrow\left[{}\begin{matrix}x=0\\x=\dfrac{2}{5}\\x=-\dfrac{2}{5}\end{matrix}\right.\\ e,Sửa:\left(4x-3\right)^2-3x\left(3-4x\right)=0\\ \Rightarrow\left(4x-3\right)^2+3x\left(4x-3\right)=0\\ \Rightarrow\left(4x-3\right)\left(7x-3\right)=0\Rightarrow\left[{}\begin{matrix}x=\dfrac{3}{4}\\x=\dfrac{3}{7}\end{matrix}\right.\)

a.

4x(x-5) - (x-1)(4x-3)-5=0

 4x^2-20x-4x^2+3x+4x+3=0

(4x^2-4x^2)+(-20x+3x+4x)+3=0

 13x+3 = 0

13x=-3

x=-3/13

b,

(3x-4)(x-2)-3x(x-9)+3=0

3x^2-6x-4x+8 - 3x^2+27x+3=0

(3x^2-3x^2)+(-6x-4x+27x)+(8+3)=0

17x+11=0

17x=-11

x=-11/17

c, 2(x+3)-x^2-3x=0

2(x+3) - x(x+3)=0

(x+3)(2-x)=0

TH1: x+3 = 0; x=-3

TH2: 2-x=0;x=2