\(1,ĐK:x\ge2\\ PT\Leftrightarrow\sqrt{3x-6}+x-2-\left(\sqrt{2x-3}-1\right)=0\\ \Leftrightarrow\dfrac{3\left(x-2\right)}{\sqrt{3x-6}}+\left(x-2\right)-\dfrac{2\left(x-2\right)}{\sqrt{2x-3}+1}=0\\ \Leftrightarrow\left(x-2\right)\left(\dfrac{3}{\sqrt{3x-6}}-\dfrac{2}{\sqrt{2x-3}+1}+1\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}x=2\left(tm\right)\\\dfrac{3}{\sqrt{3x-6}}-\dfrac{2}{\sqrt{2x-3}+1}+1=0\left(1\right)\end{matrix}\right.\)

Với \(x>2\Leftrightarrow-\dfrac{2}{\sqrt{2x-3}+1}>-\dfrac{2}{1+1}=-1\left(3x-6\ne0\right)\)

\(\Leftrightarrow\left(1\right)>0-1+1=0\left(vn\right)\)

Vậy \(x=2\)

\(2,ĐK:x\ge-1\)

Đặt \(\left\{{}\begin{matrix}\sqrt{x+1}=a\\\sqrt{x^2-x+1}=b\end{matrix}\right.\left(a,b\ge0\right)\Leftrightarrow a^2+b^2=x^2+2\)

\(PT\Leftrightarrow2a^2+2b^2-5ab=0\\ \Leftrightarrow\left(a-2b\right)\left(2a-b\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}a=2b\\b=2a\end{matrix}\right.\)

Với \(a=2b\Leftrightarrow x+1=4x^2-4x+4\left(vn\right)\)

Với \(b=2a\Leftrightarrow4x+4=x^2-x+1\Leftrightarrow x^2-5x-3=0\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{5+\sqrt{37}}{2}\left(tm\right)\\x=\dfrac{5-\sqrt{37}}{2}\left(tm\right)\end{matrix}\right.\)

Vậy ...

\(3,ĐK:x\ge-1\\ PT\Leftrightarrow3\left(x^2-x+1\right)-2\left(x+1\right)=5\sqrt{x^3+1}\) 

Đặt \(\left\{{}\begin{matrix}\sqrt{x+1}=a\\\sqrt{x^2-x+1}=b\end{matrix}\right.\left(a,b\ge0\right)\)

\(PT\Leftrightarrow3b^2-2a^2=5ab\\ \Leftrightarrow2a^2+5ab-3b^2=0\\ \Leftrightarrow\left[{}\begin{matrix}a=2b\\a=-3b\left(vn\right)\end{matrix}\right.\Leftrightarrow a=2b\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{5+\sqrt{37}}{2}\\x=\dfrac{5-\sqrt{37}}{2}\end{matrix}\right.\left(\text{giống bài 2}\right)\)

B2: a) \(\left(x+\dfrac{1}{2}\right)\left(\dfrac{1}{2}-x\right)\)

\(=-\left(x+\dfrac{1}{2}\right)\left(x-\dfrac{1}{2}\right)\)

\(=-x^2+\dfrac{1}{4}\)

b) \(\left(3x-2y\right)\left(3x+2y\right)\)

\(=\left(3x\right)^2-\left(2y\right)^2\)

\(=9x^2-4y^2\)

c) \(\left(x-3\right)\left(3+x\right)\)

\(=x^2-3^2\)

\(=x^2-9\)

d) \(x^2+6x+9\)

\(=x^2+2\cdot3\cdot x+3^2\)

\(=\left(x+3\right)^2\)

e) \(9x^2-6x+1\)

\(=\left(3x\right)^2-2\cdot3x\cdot1+1^2\)

\(=\left(3x-1\right)^2\)

f) \(x^2y^2+xy+\dfrac{1}{4}\)

\(=\left(xy\right)^2+2\cdot\dfrac{1}{2}\cdot xy+\left(\dfrac{1}{2}\right)^2\)

\(=\left(xy+\dfrac{1}{2}\right)^2\)

g) \(\left(x-y\right)^2+6\left(x-y\right)+9\)

\(=\left(x-y\right)^2+2\cdot3\cdot\left(x-y\right)+3^2\)

\(=\left(x-y+3\right)^2\)

h) \(x^2+8x+16\)

\(=x^2+2\cdot4\cdot x+4^2\)

\(=\left(x+4\right)^2\)

i) \(9x^2-24x+16\)

\(=\left(3x\right)^2-2\cdot3x\cdot4+4^2\)

\(=\left(3x-4\right)^2\)

k) \(x^2-3x+\dfrac{9}{4}\)

\(=x^2-2\cdot\dfrac{3}{2}\cdot x+\left(\dfrac{3}{2}\right)^2\)

\(=\left(x-\dfrac{3}{2}\right)^2\)

l) \(4x^2y^4-4xy^3+y^2\)

\(=\left(2xy^2\right)^2-2\cdot2xy^2\cdot y+y^2\)

\(=\left(2xy^2-y\right)^2\)

m) \(9x^2-6x+1\)

\(=\left(3x\right)^2-2\cdot3x\cdot1+1\)

\(=\left(3x-1\right)^2\)

4:

a: Xét ΔEFA và ΔAMC có

góc EFA=góc AMC(=góc EIM)

góc EAF=góc ACM

=>ΔEFA đồng dạng với ΔAMC

=>EF/AM=EA/AC

=>EF*AC=AM*EA

b: ΔEFA đồng dạng với ΔAMC

=>S EFA/S AMC=(EF/AM)^2=1/9

=>S EFA=1/9*S AMC

mà S AMC=1/2*S ABC

nên S EFA=1/9*1/2*S ABC=1/18*S ABC

=(9/25 + 16/25) + ( 2/11 + 9/11)+ (10/17 + 7/17)

= 1    +     1       +          1

= 3

Toán này đâu khó!

1=1=1=3

\(\dfrac{9}{25}+\dfrac{2}{11}+\dfrac{10}{17}+\dfrac{16}{25}+\dfrac{9}{11}+\dfrac{7}{17}\)

\(=\left(\dfrac{9}{25}+\dfrac{16}{25}\right)+\left(\dfrac{2}{11}+\dfrac{9}{11}\right)+\left(\dfrac{10}{17}+\dfrac{7}{17}\right)\)

\(=1+1+1\)

\(=3\)

\(\frac{7}{x}=\frac{y}{27}=-\frac{42}{54}\)

\(\Leftrightarrow\frac{7}{x}=\frac{y}{27}=-\frac{7}{9}\)

Có \(\frac{7}{x}=-\frac{7}{9}\)

\(\Leftrightarrow x=-9\)

Lại có \(\frac{y}{27}=-\frac{7}{9}\)

\(\Leftrightarrow x=-21\)

X= -9, Y= -21   CHƯA CHẮC ĐÂY ĐẤY

Ta có:

7/x = -42/54 \(\Rightarrow\) x =  -9 (vì 7. 54 = 378 ; 378 :(-42) = -9

7/-9 = y/27   \(\Rightarrow\)y =  -21 (vì 7.27 = 189 ; 189 : (-9) = -21

                                                   Vậy x = -9 ; y = -21.

Bài 5:

a, Áp dụng PTG: \(BC=\sqrt{AB^2+AC^2}=5\left(cm\right)\)

\(\sin B=\dfrac{AC}{BC}=\dfrac{3}{5}\approx\sin37^0\\ \Rightarrow\widehat{B}\approx37^0\\ \Rightarrow\widehat{C}\approx90^0-37^0=53^0\)

b, Áp dụng HTL: \(S_{AHC}=\dfrac{1}{2}AH\cdot HC=\dfrac{1}{2}\cdot\dfrac{AB\cdot AC}{BC}\cdot\dfrac{AC^2}{BC}=\dfrac{1}{2}\cdot\dfrac{12}{5}\cdot\dfrac{9}{5}=\dfrac{54}{25}\left(cm^2\right)\)

c, Vì AD là p/g nên \(\dfrac{DH}{DB}=\dfrac{AH}{AB}\)

Mà \(AC^2=CH\cdot BC\Leftrightarrow\dfrac{HC}{AC}=\dfrac{AC}{BC}\)

Mà \(AH\cdot BC=AB\cdot AC\Leftrightarrow\dfrac{AH}{AB}=\dfrac{AC}{BC}\)

Vậy \(\dfrac{DH}{DB}=\dfrac{HC}{AC}\)

Bài 1:

\(a,A=6\sqrt{2}-6\sqrt{2}+2\sqrt{5}=2\sqrt{5}\\ b,B=\dfrac{\sqrt{3}\left(\sqrt{3}-1\right)}{\sqrt{3}-1}+\dfrac{\sqrt{2}\left(\sqrt{2}-1\right)}{\sqrt{2}-1}=\sqrt{3}+\sqrt{2}\\ c,=2\sqrt{3}-6\sqrt{3}+15\sqrt{3}-4\sqrt{3}=7\sqrt{3}\\ d,=1+6\sqrt{3}-\sqrt{3}-1=5\sqrt{3}\\ e,=4\sqrt{2}+\sqrt{2}-6\sqrt{2}+3\sqrt{2}=2\sqrt{2}\)

Bài 2:

\(a,ĐK:x\ge\dfrac{3}{2}\\ PT\Leftrightarrow\sqrt{2x-3}=5\Leftrightarrow2x-3=25\Leftrightarrow x=14\\ b,PT\Leftrightarrow x^2=\sqrt{\dfrac{98}{2}}=\sqrt{49}=7\Leftrightarrow\left[{}\begin{matrix}x=\sqrt{7}\\x=-\sqrt{7}\end{matrix}\right.\\ c,ĐK:x\ge3\\ PT\Leftrightarrow\sqrt{x-3}\left(\sqrt{x+3}+1\right)=0\\ \Leftrightarrow\sqrt{x-3}=0\left(\sqrt{x+3}+1>0\right)\\ \Leftrightarrow x=3\\ d,ĐK:x\ge1\\ PT\Leftrightarrow2\sqrt{x-1}-\sqrt{x-1}+3\sqrt{x-1}=4\\ \Leftrightarrow\sqrt{x-1}=1\Leftrightarrow x=2\left(tm\right)\\ e,PT\Leftrightarrow2x-1=16\Leftrightarrow x=\dfrac{17}{2}\\ f,PT\Leftrightarrow\left|2x-1\right|=\sqrt{3}-1\Leftrightarrow\left[{}\begin{matrix}2x-1=\sqrt{3}-1\\2x-1=1-\sqrt{3}\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{\sqrt{3}}{2}\\x=\dfrac{2-\sqrt{3}}{2}\end{matrix}\right.\)

Bài 3:

\(a,Q=\dfrac{1+5}{3-1}=3\\ b,P=\dfrac{x+\sqrt{x}-6+x-2\sqrt{x}-3-x+4\sqrt{x}+9}{\left(\sqrt{x}-3\right)\left(\sqrt{x}+3\right)}\\ P=\dfrac{\sqrt{x}\left(\sqrt{x}+3\right)}{\left(\sqrt{x}-3\right)\left(\sqrt{x}+3\right)}=\dfrac{\sqrt{x}}{\sqrt{x}-3}\\ c,M=\dfrac{\sqrt{x}}{\sqrt{x}-3}\cdot\dfrac{3-\sqrt{x}}{\sqrt{x}+5}=\dfrac{-\sqrt{x}}{\sqrt{x}+5}\)

Vì \(-\sqrt{x}\le0;\sqrt{x}+5>0\) nên \(M< 0\)

Do đó \(\left|M\right|>\dfrac{1}{2}\Leftrightarrow M< -\dfrac{1}{2}\Leftrightarrow-\dfrac{\sqrt{x}}{\sqrt{x}+5}+\dfrac{1}{2}< 0\)

\(\Leftrightarrow\dfrac{2\sqrt{x}-\sqrt{x}-5}{2\left(\sqrt{x}+5\right)}< 0\Leftrightarrow\sqrt{x}-5< 0\left(\sqrt{x}+5>0\right)\\ \Leftrightarrow0\le x< 25\)

Bài 4:

\(a,A=\dfrac{16+2\cdot4+5}{4-3}=29\\ b,B=\dfrac{2\sqrt{x}-9-x+9+2x-3\sqrt{x}-2}{\left(\sqrt{x}-2\right)\left(\sqrt{x}-3\right)}\\ B=\dfrac{x-\sqrt{x}-2}{\left(\sqrt{x}-2\right)\left(\sqrt{x}-3\right)}=\dfrac{\left(\sqrt{x}-2\right)\left(\sqrt{x}+1\right)}{\left(\sqrt{x}-2\right)\left(\sqrt{x}-3\right)}=\dfrac{\sqrt{x}+1}{\sqrt{x}-3}\\ c,P=\dfrac{x+2\sqrt{x}+5}{\sqrt{x}-3}\cdot\dfrac{\sqrt{x}-3}{\sqrt{x}+1}=\dfrac{x+2\sqrt{x}+5}{\sqrt{x}+1}\\ P=\dfrac{\left(\sqrt{x}+1\right)^2+4}{\sqrt{x}+1}=\sqrt{x}+1+\dfrac{4}{\sqrt{x}+1}\\ P\ge2\sqrt{\left(\sqrt{x}+1\right)\cdot\dfrac{4}{\sqrt{x}+1}}=2\sqrt{4}=4\\ P_{min}=4\Leftrightarrow\left(\sqrt{x}+1\right)^2=4\Leftrightarrow\sqrt{x}+1=2\Leftrightarrow x=1\left(tm\right)\)

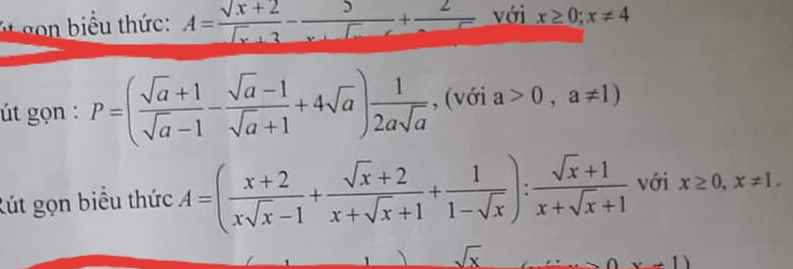
\(A=\left(\dfrac{x+2}{x\sqrt{x}-1}+\dfrac{\sqrt{x}+2}{x+\sqrt{x}+1}+\dfrac{1}{1-\sqrt{x}}\right):\dfrac{\sqrt{x}+1}{x+\sqrt{x}+1}\)

    \(=\left[\dfrac{x+2}{\sqrt{x^3}-1}+\dfrac{\left(\sqrt{x}+2\right)\left(\sqrt{x}-1\right)}{\sqrt{x^3}-1}-\dfrac{x+\sqrt{x}+1}{\sqrt{x^3}-1}\right]:\dfrac{\sqrt{x}+1}{x+\sqrt{x}+1}\)

    \(=\left(\dfrac{x+2+x-\sqrt{x}+2\sqrt{x}-2-x-\sqrt{x}-1}{\sqrt{x^3}-1}\right):\dfrac{\sqrt{x}+1}{x+\sqrt{x}+1}\)

    \(=\dfrac{x-1}{\left(\sqrt{x}-1\right)\left(x+\sqrt{x}+1\right)}.\dfrac{x+\sqrt{x}+1}{\sqrt{x}+1}\)

    \(=1\)

\(P=\left(\dfrac{\sqrt{a}+1}{\sqrt{a}-1}-\dfrac{\sqrt{a}-1}{\sqrt{a}+1}+4\sqrt{a}\right).\dfrac{1}{2a\sqrt{a}}\)

    \(=\left[\dfrac{\left(\sqrt{a}+1\right)^2}{a-1}-\dfrac{\left(\sqrt{a}-1\right)^2}{a-1}+\dfrac{4\sqrt{a}\left(a-1\right)}{a-1}\right].\dfrac{1}{2a\sqrt{a}}\)

\(=\left(\dfrac{a+2\sqrt{a}+1-a+2\sqrt{a}-1+4a\sqrt{a}-4\sqrt{a}}{a-1}\right).\dfrac{1}{2a\sqrt{a}}\)

\(=\dfrac{4a\sqrt{a}}{a-1}.\dfrac{1}{2a\sqrt{a}}\)

\(=\dfrac{2}{a-1}\)