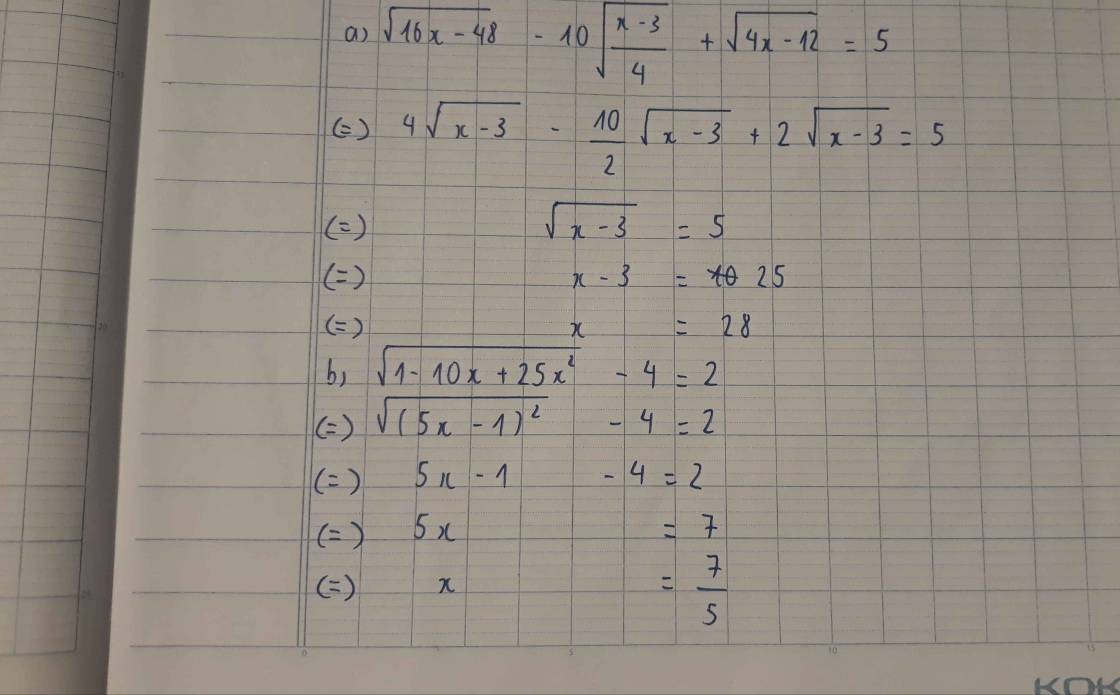a) \(\sqrt{4x^2+4x+1}=6\)

\(\Leftrightarrow\sqrt{\left(2x+1\right)^2}=6\)

\(\Leftrightarrow\left(2x+1\right)^2=6^2\)

\(\Leftrightarrow\left[{}\begin{matrix}2x+1=6\\2x+1=-6\end{matrix}\right.\)

\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{5}{2}\\x=-\dfrac{7}{2}\end{matrix}\right.\)

b) \(\sqrt{4x^2-4\sqrt{7}x+7}=\sqrt{7}\)

\(\Leftrightarrow\sqrt{\left(2x-\sqrt{7}\right)^2}=\sqrt{7}\)

\(\Leftrightarrow\left(2x-\sqrt{7}\right)^2=\left(\sqrt{7}\right)^2\)

\(\Leftrightarrow\left[{}\begin{matrix}2x-\sqrt{7}=\sqrt{7}\\2x-\sqrt{7}=-\sqrt[]{7}\end{matrix}\right.\)

\(\Leftrightarrow\left[{}\begin{matrix}x=\sqrt{7}\\x=0\end{matrix}\right.\)

a) \(\sqrt{4x^2+4x+1}=6\)

\(\Leftrightarrow\sqrt{\left(2x+1\right)^2}=6\)

\(\Leftrightarrow\left|2x+1\right|=6\)

\(\Leftrightarrow\left[{}\begin{matrix}2x+1=6\\2x+1=-6\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{5}{2}\\x=-\dfrac{7}{2}\end{matrix}\right.\)

b) \(pt\Leftrightarrow\sqrt{\left(2x-\sqrt{7}\right)^2}=\sqrt{7}\)

\(\Leftrightarrow\left|2x-\sqrt{7}\right|=\sqrt{7}\)

\(\Leftrightarrow\left[{}\begin{matrix}2x-\sqrt{7}=\sqrt{7}\\2x-\sqrt{7}=-\sqrt{7}\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=\sqrt{7}\\x=0\end{matrix}\right.\)

c) \(PT\Leftrightarrow\sqrt{\left(x+\sqrt{3}\right)^2}=2\sqrt{3}\)

\(\Leftrightarrow\left|x+\sqrt{3}\right|=2\sqrt{3}\)

\(\Leftrightarrow\left[{}\begin{matrix}x+\sqrt{3}=2\sqrt{3}\\x+\sqrt{3}=-2\sqrt{3}\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=\sqrt{3}\\x=-3\sqrt{3}\end{matrix}\right.\)

d) \(pt\Leftrightarrow\left|x-3\right|=9\Leftrightarrow\left[{}\begin{matrix}x-3=-9\\x-3=9\end{matrix}\right.\)

\(\Leftrightarrow\left[{}\begin{matrix}x=-6\\x=12\end{matrix}\right.\)

a: Đặt \(x^2-4=a\)

Pt sẽ là \(a=3\sqrt{xa}\)

\(\Rightarrow a^2=9xa\)

\(\Leftrightarrow a\left(a-9x\right)=0\)

\(\Leftrightarrow\left(x^2-4\right)\left(x^2-4-9x\right)=0\)

hay \(x\in\left\{2;-2;\dfrac{9+\sqrt{97}}{2};\dfrac{9-\sqrt{97}}{2}\right\}\)

d: Đặt \(\sqrt{x^2-x+1}=a;\sqrt{x^2+x+1}=b\)

Pt sẽ là 2a+b=ab+2

=>(b-2)(1-a)=0

=>b=2 và 1-a

\(\Leftrightarrow\left\{{}\begin{matrix}x^2+x+1=4\\x^2-x+1=1\end{matrix}\right.\Leftrightarrow x\in\varnothing\)

bạn tách từng câu ra mik suy nghĩ từng câu

Câu 3: đề là \(\sqrt{x+5}-\sqrt{x-2}\) hay \(\sqrt{x+5}-\sqrt{x+2}\)?

Câu 4:

ĐKXĐ: \(x\le9\)

Đặt \(\left\{{}\begin{matrix}\sqrt[3]{x-4}=a\\\sqrt{9-x}=b\end{matrix}\right.\) ta có hệ:

\(\left\{{}\begin{matrix}a-b=-1\\a^3+b^2=5\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}b=a+1\\a^3+b^2=5\end{matrix}\right.\)

\(\Rightarrow a^3+\left(a+1\right)^2=5\)

\(\Leftrightarrow a^3+a^2+2a-4=0\) \(\Rightarrow a=1\)

\(\Rightarrow\sqrt[3]{x-4}=1\Rightarrow x-4=1\Rightarrow x=5\)

5.

ĐKXĐ: \(x\ge-\frac{17}{16}\)

\(\Leftrightarrow8x^2-15x-23-\left(x+1\right)\sqrt{16x+17}=0\)

\(\Leftrightarrow\left(x+1\right)\left(8x-23\right)-\left(x+1\right)\sqrt{16x+17}=0\)

\(\Leftrightarrow\left[{}\begin{matrix}x=-1\\8x-23=\sqrt{16x+17}\left(1\right)\end{matrix}\right.\)

\(\left(1\right)\Leftrightarrow16x+17-2\sqrt{16x+17}-63=0\)

Đặt \(\sqrt{16x+17}=t\ge0\)

\(\Rightarrow t^2-2t-63=0\Rightarrow\left[{}\begin{matrix}t=9\\t=-7\left(l\right)\end{matrix}\right.\)

\(\Rightarrow\sqrt{16x+17}=9\Leftrightarrow x=\frac{32}{3}\)

mình cần phần 3 4 5 nữa thui ạ

Giải bằng bất đẳng thức Cô si: (ĐK: \(x^2-x+1\ge0;-2x^2+x+2\ge0;x^2-4x+7\)
Ta có: \(x^2-x+1+1\ge2\sqrt{x^2-x+1}\Leftrightarrow\sqrt{x^2-x+1}\le\dfrac{x^2-x+2}{2}\left(1\right)\\ T,T:\sqrt{-2x^2+x+2}\le\dfrac{-2x^2+x+3}{2}\left(2\right)\\ \left(1\right);\left(2\right)\Rightarrow\sqrt{x^2-x+1}+\sqrt{-2x^2+x+2}\le\dfrac{x^2-x+2-2x^2+x+3}{2}=\dfrac{-x^2+5}{2}\\ \Rightarrow\sqrt{x^2-x+1}+\sqrt{-2x^2+x+2}-\dfrac{x^2-4x+7}{2}\le\dfrac{-x^2+5-x^2+4x-7}{2}\\ =\dfrac{-2x^2+4x-2}{2}\\ =-x^2+2x-1 \\ \Rightarrow-\left(x-1\right)^2\ge0\)
Điều này chỉ thỏa 1 điều kiên khi x-1=0 ⇔x=1(nhận
Vậy x=1 là nghiệm cuả phương trình

\(x=1\)

lm jup mk di m.n