Cho tam giác đều ABC có cạnh bằng a, H là trung điểm cạnh BC. vtCH + vtCH có độ dài bao nhiêu.
Cho tam giác đều ABC có cạnh bằng a H là trung điểm của BC. Độ dài của C A → - H C → là
A . a 2
B . 3 a 2
C . 2 3 3 a
D . a 7 2
cho tam giác đều ABC có cạnh bằng a ,H là trung điểm của BC.Vecto CH + vecto CH có độ dài là:
\(\left|\overrightarrow{CH}+\overrightarrow{CH}\right|=a\)
Cho ABC có B B = 60 , A = 2 cm,BC = 5 cm. Trên cạnh BC lấy điểm D sao cho
BA BD = .
a) Chứng minh tam giác ABD đều;
b) Gọi H là trung điểm của BD. Chứng minh AH BD ⊥ ;
c) Tính độ dài cạnh AC;
d) Tam giác ABC có là tam giác vuông không? Tại sao?
Cho lăng trụ ABC.A'B'C' có độ dài cạnh bên bằng 2a, đáy ABC là tam giác đều cạnh a và hình chiếu vuông góc của đỉnh A’ trên mặt phẳng (ABC) là trung điểm cạnh BC. Thể tích khối chóp A.BCC’B’ là:
A. a 3 39 8
B. a 3 39 16
C. a 3 39 36
D. a 3 39 12
Đáp án D
Gọi H là trung điểm của BC, khi đó từ giả thiết ta có A'H ⊥ (ABC). Ta có:
A'H = a 3 => V A . BCC ' B ' = V ABC . A ' B ' C ' - V A ' . ABC
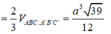
Cho tam giác đều \(ABC\) có độ dài cạnh bằng \(a\). Gọi \(M\) là 1 điểm nằm trong tam giác. \(MI,MP,MQ\) theo thứ tự là khoảng cách từ \(M\) đến các cạnh \(BC,AB,AC\). Gọi \(O\) là trung điểm của cạnh \(BC\). Các điểm \(D\) và \(E\) theo thứ tự chuyển động trên các cạnh \(AB\) và \(AC\) sao cho \(\widehat{DOE}=60^o\).
\(a\)) Chứng minh: \(MI+MP+MQ\) không đổi.
\(b\)) Chứng minh: Đường thẳng \(DE\) luôn tiếp xúc với một đường tròn cố định.
\(c\)) Xác định vị trí của \(D\) và \(E\) để diện tích tam giác \(DOE\) đạt giá trị nhỏ nhất. Tính giá trị nhỏ nhất đó theo \(a\).
Cho tam giác ABC là tam giác đều cạnh a, gọi H là trung điểm cạnh BC. Hình nón nhận được khi quay tam giác ABC xung quanh trục AH có diện tích đáy bằng:
A. π a 2
B. π a 2 2
C. π a 2 4
D. π a 2
Cho tam giác đều abc có cạnh ab=4cm, gọi M là trung điểm cạnh bc .tính độ dài vecto bm-ba.
\(=\dfrac{4\sqrt{3}}{2}=2\sqrt{3}\)
Cho tam giác ABC đều cạnh bằng a, M là trung điểm của BC tính độ dài vecto AM
\(\left|\overrightarrow{AM}\right|=AM=\dfrac{a\sqrt{3}}{2}\)
Cho hình lăng trụ A B C . A ' B ' C ' có đáy là tam giác đều cạnh có độ dài bằng 2a. Hình chiếu vuông góc của A' lên mặt phẳng (ABC) trùng với trung điểm H của BC. Khoảng cách giữa hai đường thẳng BB' và A'H bằng
A. a 3 2
B. a 3 3
C. a
D. 2a