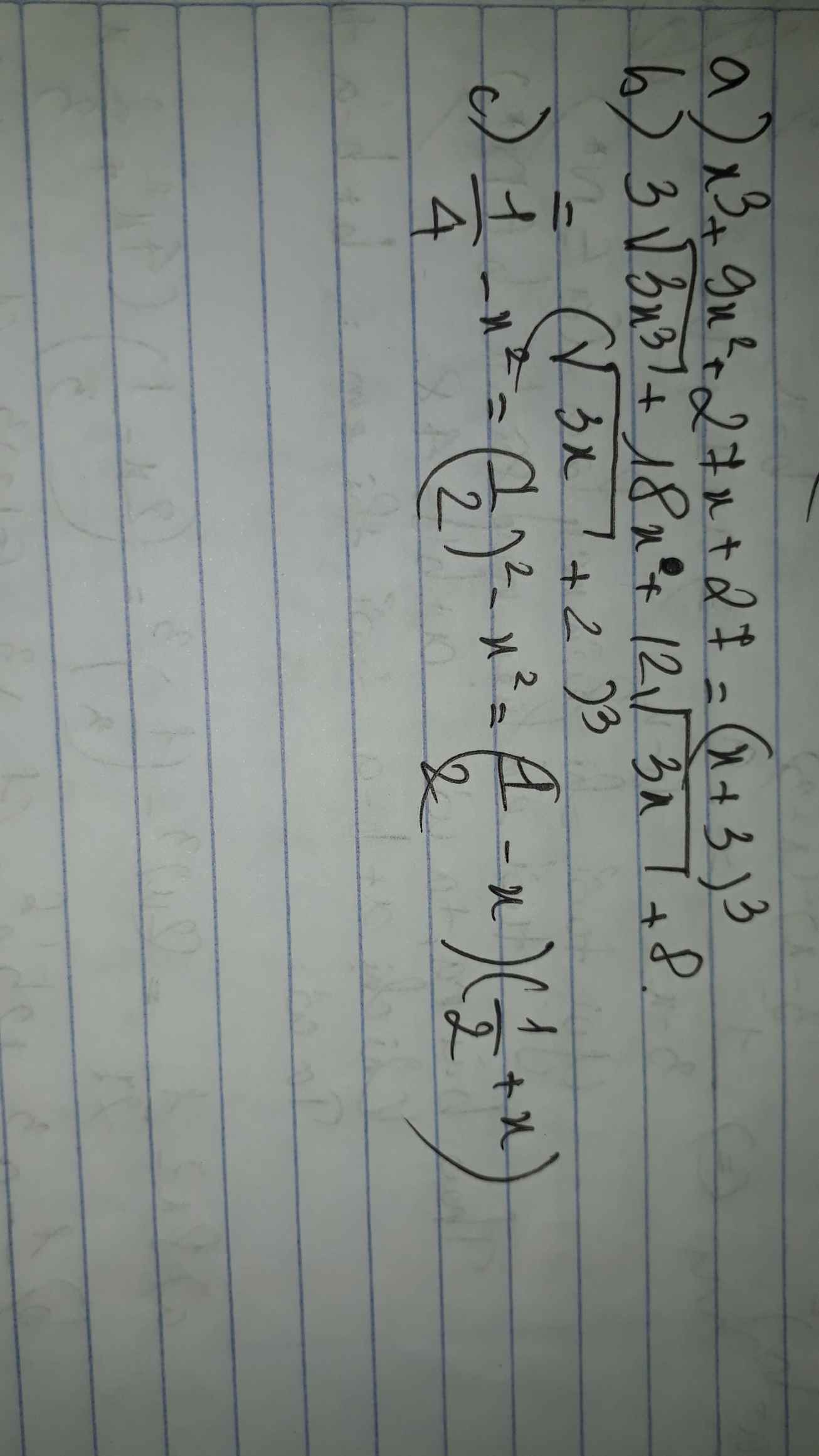a) x² + x - 12 = x² - 3x + 4x - 12 = x(x - 3) + 4(x - 3) = (x - 3)(x + 4)

b) x² - x - 12 = x² + 3x - 4x - 12 = x(x + 3) - 4(x + 3) = (x + 3)(x - 4)

c) x² - 9x + 20 = x² - 4x - 5x + 20 = x(x - 4) - 5(x - 4) = (x - 4)(x - 5)

d) x² + 9x + 20 = x² + 4x + 5x + 20 = x(x + 4) + 5(x + 4) = (x + 4)(x + 5)

a,x^2+x-12=x^2-3x+4x-12

                 =x(x-3)+4(x-3)

                 =(x-3)*(x+4)

b) x² - x - 12 = x² + 3x - 4x - 12 = x(x + 3) - 4(x + 3) = (x + 3)(x - 4)

\(\frac{12}{5}x^2y^2-9x^4-\frac{4}{25}y^4\)

\(=-\left(\frac{4}{25}y^4-\frac{12}{5}x^2y^2+9x^4\right)\)

\(=-\left[\left(\frac{2}{5}y^2\right)^2-2\cdot\frac{2}{5}y^2\cdot3x^2+\left(3x^2\right)^2\right]\)

\(=-\left(\frac{2}{5}y^2-3x^2\right)^2\)

        \(\frac{12}{5}x^2y^2-9x^4-\frac{4}{25}y^4\)

\(=-\left(9x^4-\frac{12}{5}x^2y^2+\frac{4}{25}y^4\right)\)

\(=-\left[\left(3x\right)^2-2.3x^2.\frac{2}{5}y^2+\left(\frac{2}{5}y^2\right)^2\right]\)

\(=-\left(3x^2+\frac{2}{5}y^2\right)\)

bạn tách ra từng ít câu 1 thôi ạ

a: \(=5x\left(xy^2+3x+6y^2\right)\)

b: \(=\left(x-2\right)\left(x+3\right)-\left(x-2\right)\left(x+2\right)=\left(x-2\right)\left(x+3-x-2\right)=\left(x-2\right)\)

c: \(=\left(x-3\right)\left(x-4\right)\)

d: \(=x\left(x^2-2xy+y^2-9\right)\)

=x(x-y-3)(x-y+3)

e: \(=\left(x+y\right)^2-25=\left(x+y+5\right)\left(x+y-5\right)\)

f: \(=\left(x-4\right)\left(x+3\right)\)

1) \(x^3+2x-3\)

\(=\left(x^3-x^2\right)+\left(x^2-x\right)+\left(3x-3\right)\)

\(=x^2\left(x-1\right)+x\left(x-1\right)+3\left(x-1\right)\)

\(=\left(x-1\right)\left(x^2+x+3\right)\)

2) \(x^3-6x+4\)

\(=\left(x^3-2x^2\right)+\left(2x^2-4x\right)-\left(2x-4\right)\)

\(=x^2\left(x-2\right)+2x\left(x-2\right)-2\left(x-2\right)\)

\(=\left(x-2\right)\left(x^2+2x-2\right)\)

3) \(x^3-2x^2+1\)

\(=\left(x^3-x^2\right)-\left(x^2-x\right)-\left(x-1\right)\)

\(=x^2\left(x-1\right)-x\left(x-1\right)-\left(x-1\right)\)

\(=\left(x-1\right)\left(x^2-x-1\right)\)

4) \(x^3+5x^2-12\)

\(=\left(x^3+2x^2\right)+\left(3x^2+6x\right)-\left(6x+12\right)\)

\(=x^2\left(x+2\right)+3x\left(x+2\right)-6\left(x+2\right)\)

\(=\left(x+2\right)\left(x^2+3x-6\right)\)

5) \(x^3-6x^2+9x\) (chắc đề như vậy)

\(=x\left(x^2-6x+9\right)\)

\(=x\left(x-3\right)^2\)

6) \(4x^3-9x^2+5x\)

\(=x\left(4x^2-9x+5\right)\)

\(=x\left[\left(4x^2-4x\right)-\left(5x-5\right)\right]\)

\(=x\left[4x\left(x-1\right)-5\left(x-1\right)\right]\)

\(=x\left(x-1\right)\left(4x-5\right)\)

1/ Đặt x²+x=t

=>(x²+x)²+4(x²+x)-12=t²+4t-12=t²+6t-2t-12=t(t+6)-2(t+6)=(t-2)(t+6)=(x²+x-2)(x²+x+6)=(x²-x+2x-2)(x²+x+6)

=[x(x-1)+2(x-1)](x²+x+6)=(x-1)(x+2)(x²+x+6)

2/ Đặt x²+x=t 

=>(x²+x)²+9x²+9x+14=(x²+x)²+9(x²+x)+14=t²+9t+14=t²+2t+7t+14=t(t+2)+7(t+2)=(t+2)(t+7)=(x²+x+2)(x²+x+7)

3/ Đặt x²+5x=t

=>(x²+5x)²+10x²+50x+24=(x²+5x)²+10(x²+5x)+24=t²+10t+24=t²+4t+6t+24=t(t+4)+6(t+4)=(t+4)(t+6)=(x²+5x+4)(x²+5x+6)

=(x²+x+4x+4)(x²+2x+3x+6)=[x(x+1)+4(x+1][x(x+2)+3(x+2)]=(x+1)(x+4)(x+2)(x+3)=(x+1)(x+2)(x+3)(x+4)

Bài 1:

\(=\left(3x-1\right)^2-9y^2\)

=(3x-1-3y)(3x-1+3y)

=(3x-1-3y)(3x-1+3y)
Tham khảo ạ

=(3x-1-3y)(3x-1+3y)

HT

Câu b đề sai nha bạn.

a) \(x^3+9x^2+27x+27=\left(x+3\right)^3\)

b) \(3\sqrt{3x^3}+18x^2+12\sqrt{3x}+8=\left(\sqrt{3x}+2\right)^3\)

c) \(\dfrac{1}{4}-x^2=\left(\dfrac{1}{2}-x\right)\left(\dfrac{1}{2}+x\right)\)