chứng minh 2x/2√x =4

Những câu hỏi liên quan
1.chứng minh \(\dfrac{6x^3-x^6}{x^4-2x^2+4}< 3\) với mọi x ∈ R
2.chứng minh \(\dfrac{x^4-4x^2+8}{2x-x^2}>4\) với mọi x ∈ (0;2)
Chứng minh rằng(3x-5)(2x+1)-(2x-1)^2-2x(x-2)-x+10=4
(3x-5)(2x+1)-(2x-1)^2-2x(x-2)-x+10=4
=>6x^2+3x-10x-5-(4x^2-4x+1)-2x^2+4x-x+10=4
=>(6x^2-4x^2-2x^2)+(3x-10x+4x+4x-x)+(-5-1+10)=4
=>4=4
Đúng 1
Bình luận (0)
Chứng minh đẳng thức:
4 x x 2 - 4 + x x + 2 + 2 x - 2 = x + 2 x - 2
Biến đổi vế trái (VT), ta có: MTC = x2 – 4.
4
x
x
2
-
4
+
x
x
+
2
+
2
x
-
2
=
x
+
2
x
-
2
![]()
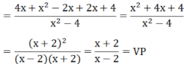
Đúng 0
Bình luận (0)
Chứng minh rằng (x+1)2=x2+2x+1 và chứng minh đa thức P(x)=x2+2x+4 không có nghiệm.
Mik cảm ơn trước
\(\left(x+1\right)^2=x^2+2\cdot x\cdot1+1^2=x^2+2x+1=VP\left(đpcm\right)\)
\(P\left(x\right)=x^2+2x+4\)
\(\Delta=b^2-4ac=2^2-4\cdot1\cdot4=4-16=-12\)
\(\Delta< 0\)=> Đa thức vô nghiệm ( đpcm )
\(\left(x+1\right)^2=\left(x+1\right)\left(x+1\right)=x^2+x+x+1=x^2+2x+1\)
=> \(x^2+2x+1=x^2+2x+1\left(\text{đ}pcm\right)\)
Ta có : \(P\left(x\right)=x^2+2x+4=0\)
\(\hept{\begin{cases}x^2\ge0\\2x\ge0\\4>0\end{cases}\Rightarrow vonghiem}\)
Ê Tú ... Ai dạy mi \(2x\ge0\)đấy :)
Cách khác delta
\(P\left(x\right)=x^2+2x+4\)
\(P\left(x\right)=x^2+2x+1+3\)
\(P\left(x\right)=\left(x+1\right)^2+3\)
\(\hept{\begin{cases}\left(x+1\right)^2\ge0\forall x\\3>0\end{cases}}\Rightarrow\left(x+1\right)^2+3\ge3>0\forall x\)
=> đpcm
Xem thêm câu trả lời
| Chứng minh đẳng thức |
| x2 – 4 + ( x – 2 )2 = 2x ( x – 2 ) |
x2 - 4 + (x - 2)2
= (x - 2)(x + 2) + (x - 2)2
= (x - 2)(x + 2 + x - 2)
= 2x(x - 2)
Vậy x2 - 4 + (x - 2)2 = 2x(x - 2)
Đúng 0
Bình luận (1)
chứng minh giá trị biểuthức ko phụ thuộc giá trị biến x
(x mũ 2 -5x+4) (2x+4) -(2x mũ 2-x-10) (x-3)
\(\text{∘ Ans}\)
\(\downarrow\)
\(\left(x^2-5x+4\right)\left(2x+4\right)-\left(2x^2-x-10\right)\left(x-3\right)\)
`= 2x(x^2 - 5x + 4) + 4(x^2 - 5x + 4) - [x(2x^2 - x - 10) - 3(2x^2 - x - 10) ]`
`= 2x^3 - 10x^2 + 8x + 4x^2 - 20x + 16 - (2x^3 - x^2 - 10x - 6x^2 + 3x + 30)`
`= 2x^3 - 6x^2 - 12x + 16 - 2x^3 + x^2 + 10x + 6x^2 - 3x - 30`
`= (2x^3 - 2x^3) + (-6x^2 + 6x^2 + x^2) + (-12x + 10x - 3x) + (16 - 30)`
`= x^2 - 5x - 14`
Bạn xem lại đề.
Đúng 1
Bình luận (0)
bài 1: chứng minh :(a+b)2-(a-b)24abrút gọn :(a+2)2_(a+2).(a-2)tìm x: (2x+3)2-4(x-1).(x+1)49tính giá trị biểu thức :Q(x+3)2+(x+3).(x-3)-2.(x+2).(x-4), cho x1/2bài 2rút gọn biểu thức A(4x2+y2).(2x+y).(2x-y)chứng minh :(7x+1)2-(x+7)2+48(x2-1)tìm x, biết : 16x2-(4x-5)215tìm giá trị nhỏ nhất : A-x2+2x+3Em đang cần gấp! giúp với ạ
Đọc tiếp
bài 1:
chứng minh :(a+b)2-(a-b)2=4ab
rút gọn :(a+2)2_(a+2).(a-2)
tìm x: (2x+3)2-4(x-1).(x+1)=49
tính giá trị biểu thức :
Q=(x+3)2+(x+3).(x-3)-2.(x+2).(x-4), cho x=1/2
bài 2
rút gọn biểu thức
A=(4x2+y2).(2x+y).(2x-y)
chứng minh :(7x+1)2-(x+7)2+48(x2-1)
tìm x, biết : 16x2-(4x-5)2=15
tìm giá trị nhỏ nhất : A-x2+2x+3
Em đang cần gấp! giúp với ạ
chứng minh x^4+2x^3-2x^2-10x+20>0với mọi x
chứng minh rằng √(x^2+2x+5) +√(2x^2+4x+6) ≥ 4
\(VT=\sqrt{x^2+2x+5}+\sqrt{2x^2+4x+6}\)
\(=\sqrt{x^2+2x+1+4}+\sqrt{2x^2+4x+2+4}\)
\(=\sqrt{\left(x+1\right)^2+4}+\sqrt{2\left(x+1\right)^2+4}\)
Dễ thấy: \(\hept{\begin{cases}\sqrt{\left(x+1\right)^2}\ge0\\\sqrt{2\left(x+1\right)^2}\ge0\end{cases}}\)\(\Rightarrow\hept{\begin{cases}\sqrt{\left(x+1\right)^2+4}\ge\sqrt{4}=2\\\sqrt{2\left(x+1\right)^2+4}\ge\sqrt{4}=2\end{cases}}\)
\(\Rightarrow\sqrt{\left(x+1\right)^2+4}+\sqrt{2\left(x+1\right)^2+4}\ge2+2=4\)
Đẳng thức xảy ra khi \(x=-1\)
Đúng 0
Bình luận (0)
1.Chứng minh tích của 2,3,4 số nguyên dương liên tiếp ko là số chính phương.
2.Chứng minh với mọi x thuộc N* thì x^4+2x^3+2x^2+2x+1 ko là số chính phương
Dây là 4 số nguyên dương liên tiếp, còn phần kia tương tự nha
Đặt A = n.(n+1)(n+2)(n+3) với n ≥ 1; n € N
A = [n.(n+3)].[(n+1)(n+2)] = (n² + 3n).(n²+3n+2)
= t(t+2) (với t = n² + 3n ≥ 4 ; t € N)
Ta thấy
t² < A = t² + 2t < t² + 2t + 1 = (t+1)²
=> A nằm giữa 2 số chính phương liên tiếp
=> A không phải là số chính phương (đpcm)
Đúng 1
Bình luận (0)

























