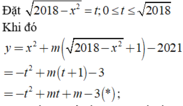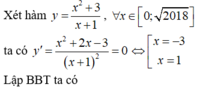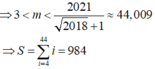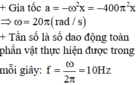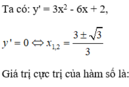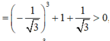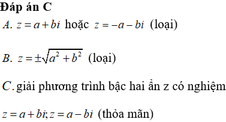Trục số thực là j

Những câu hỏi liên quan
Cho hàm số
y
x
2
+
m
(
2018
-
x
2
+
1
)
-
2021
với m là tham số thực. Gọi S là tổng tất cả các giá trị nguyên của t...
Đọc tiếp
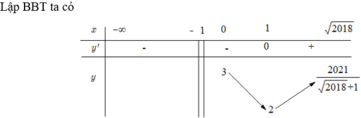
Cho hàm số y = x 2 + m ( 2018 - x 2 + 1 ) - 2021 với m là tham số thực. Gọi S là tổng tất cả các giá trị nguyên của tham số m để đồ thị của hàm số đã cho cắt trục hoành tại đúng hai điểm phân biệt. Tính S.
A. 960
B. 986
C. 984
D. 990
Một vật dao động điều hoà trên trục Ox với vị trí cân bằng là gốc toạ độ. Gia tốc và li độ liên hệ với nhau bằng biểu thức
a
-
4
π
2
x
. Số dao động toàn phần vật thực hiện được trong mỗi giây là: A. 400 B. 40 C. 10 D. 20
Đọc tiếp
Một vật dao động điều hoà trên trục Ox với vị trí cân bằng là gốc toạ độ. Gia tốc và li độ liên hệ với nhau bằng biểu thức a = - 4 π 2 x . Số dao động toàn phần vật thực hiện được trong mỗi giây là:
A. 400
B. 40
C. 10
D. 20
Một vật dao động điều hoà trên trục Ox với vị trí cân bằng là gốc toạ độ. Gia tốc và li độ liên hệ với nhau bằng biểu thức
a
−
4
π
2
x
. Số dao động toàn phần vật thực hiện được trong mỗi giây là: A. 400 B. 40 C. 10 D. 20
Đọc tiếp
Một vật dao động điều hoà trên trục Ox với vị trí cân bằng là gốc toạ độ. Gia tốc và li độ liên hệ với nhau bằng biểu thức a = − 4 π 2 x . Số dao động toàn phần vật thực hiện được trong mỗi giây là:
A. 400
B. 40
C. 10
D. 20
Cho hàm số
y
x
4
2
-
2
m
2
x
2
+
2
. Tìm tập hợp tất cả các giá trị của tham số thực m sao cho đồ thị của hàm số đã cho có cực đại và cực tiểu, đồng thời đường thẳng cùng phương với trục hoành qua điểm cực đại tạo với đồ thị một hình ph...
Đọc tiếp
Cho hàm số y = x 4 2 - 2 m 2 x 2 + 2 . Tìm tập hợp tất cả các giá trị của tham số thực m sao cho đồ thị của hàm số đã cho có cực đại và cực tiểu, đồng thời đường thẳng cùng phương với trục hoành qua điểm cực đại tạo với đồ thị một hình phẳng có diện tích bằng 64 15 là
![]()
![]()
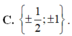
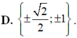
Nguyệt thực là j
Nhật thực là j
- Nhật Thực là hiện tượng Mặt Trăng làm vật cản sáng giữa Mặt Trời và Trái Đất
- Nhật thực toàn phần (hay một phần) quan sát được ở chỗ có bóng tối (hay bóng nữa tối) của Mặt Trăng trên Trái Đất.
- Nguyệt Thực xảy ra khi Mặt Trăng bị Trái Đất che khuất không được Mặt Trời chiếu sáng.
Đúng 0
Bình luận (0)
Số giao điểm của đồ thị hàm số y = x 3 - 3 x 2 + 2 x + 1 với trục hoành là
A. 0
B. 1
C. 2
D. 4
xác định hàm số bậc nhất y \(=\) ax + b, biết đồ thị hàm số có hệ số góc là -2 và cắt trục hoành tại điểm có hoành độ là 2
Hệ số góc là `-2` `=> a=-2`
Với `a=-2` ta có hàm số `y=-2x+b`
Đồ thị h/s cắt trục hoành tại điểm có hoành độ là `2` nên `y=-2x+b` đi qua điểm `(2;0)`
`0=-2*2+b`
`<=> 0 = -4+b`
`<=>b=4`
Vậy hàm số bậc nhất là : `y=-2x+4`
Đúng 3
Bình luận (0)
Cho số phức za+bi với a, b là hai số thực khác 0. Một phương trình bậc hai với hệ số thực nhận
z
làm nghiệm với mọi a, b là: A.
z
2
a
2
-
b
2
+
2
a
b
i
B.
z
2
a
2...
Đọc tiếp
Cho số phức z=a+bi với a, b là hai số thực khác 0. Một phương trình bậc hai với hệ số thực nhận z làm nghiệm với mọi a, b là:
A. z 2 = a 2 - b 2 + 2 a b i
B. z 2 = a 2 + b 2
C. z 2 - 2 a z + a 2 + b 2 = 0
D. z 2 + 2 a z + a 2 - b 2 = 0
Bài 6. Cho hàm số y = -2x + 3.
a) Vẽ đồ thị của hàm số trên.
b) Gọi A và B theo thứ tự là giao điểm của đồ thị với các trục Ox và Oy. Tính diện tích tam giác OAB (với O là gốc tọa độ và đơn vị trên các trục tọa độ là centimet ).
c) Tính độ dài đoạn AB
\(b,\text{PT giao Ox và Oy: }\\ y=0\Leftrightarrow x=\dfrac{3}{2}\Leftrightarrow A\left(\dfrac{3}{2};0\right)\Leftrightarrow OA=\dfrac{3}{2}\\ x=0\Leftrightarrow y=3\Leftrightarrow B\left(0;3\right)\Leftrightarrow OB=3\\ \Leftrightarrow S_{OAB}=\dfrac{1}{2}OA\cdot OB=\dfrac{1}{2}\cdot\dfrac{3}{2}\cdot3=\dfrac{9}{4}\left(cm^2\right)\\ c,C_1:\text{Áp dụng Pytago: }AB=\sqrt{OA^2+OB^2}=\dfrac{3\sqrt{5}}{2}\left(cm\right)\\ C_2:AB=\sqrt{\left(x_A-x_B\right)^2+\left(y_A-y_B\right)^2}=\sqrt{\left(\dfrac{3}{2}-0\right)^2+\left(0-3\right)^2}=\dfrac{3\sqrt{5}}{2}\left(cm\right)\)
Đúng 2
Bình luận (1)