Hình chữ nhật ABCD nội tiếp đường tròn ( O;R). Chứng minh rằng tổng bình phương các khoảng cách từ điểm M \(\in\) (O) đến các đường thẳng chứa cạnh của hình chữ nhật không phụ thuộc vào vị trí của M

Những câu hỏi liên quan
Cho hình chữ nhật ABCD có chu vi bằng 56cm và nội tiếp đường tròn (O) có bán kính R=10cm. Tính diện tích hình chữ nhật ABCD
Đặt AB=x; BC=y
=>x+y=28 và x^2+y^2=20^2=400
=>x=16; y=12
=>S=16*12=192cm2
Đúng 1
Bình luận (0)
Cho hình chữ nhật ABCD có chu vi bằng 28cm và nội tiếp đường tròn(O) có bán kính R=5cm. Tính diện tích hình chữ nhật ABCD
Đặt AB=x, BC=y
Theo đề, ta có:
x+y=14 và x^2+y^2=100
=>x=8; y=6
=>S=8*6=48cm2
Đúng 0
Bình luận (0)
Cho tứ giác ABCD nội tiếp đường tròn O. Gọi E,F,G,H lần lượt là tâm đường tròn nội tiếp của các tam giác ABC, BCD, CDA, DAB. CMR: EFGH là hình chữ nhật.
chứng minh các tứ giác nội tiếp sau nội tiếp được đường tròn bằng định nghĩa: A B C D ABCD là hình thang cân P Q S R PQSR là hình vuông L M O N LMNO là hình chữ nhật
Đọc tiếp
chứng minh các tứ giác nội tiếp sau nội tiếp được đường tròn bằng định nghĩa:
1. AB // CD (ABCD là hình thang) => ^B + ^D = 180o (Trong cùng phía)
Mà ^B = ^A (ABCD là hình thang) => ^A + ^D = 180o
Xét hình thang ABCD có: ^A đối diện với ^D
^A + ^D = 180o (cmt)
=> hình thang ABCD nội tiếp đường tròn
2. Xét hình chữ nhật LMNO có:
^L + ^N = 180o (^L = 90o; ^N = 90o)
=> hình chữ nhật LMNO nội tiếp đường tròn
3. Xét hình vuông PQRS có:
^P + ^R = 180o (^P = 90o; ^R = 90o)
=> hình vuông PQRS nội tiếp đường tròn
Đúng 2
Bình luận (0)
Cho tứ giác ABCD. Gọi O1, O2, O3, O4 là tâm đường tròn nội tiếp tam giác ABD, ABC, BCD, CDA. CMR: Nếu O1O2O3O4 là hình chữ nhật thì tứ giác ABCD là tứ giác nội tiếp
đề sai. muốn c/m đề sai thì nói. mình c/m cho
Hình chữ nhật ABCD nội tiếp đường tròn (O; R). Chứng minh rằng tổng bình phương các khoảng cách từ điểm M \(\in\) (O) đến các đường thẳng chứa cạnh của hình chữ nhật không phụ thuộc vào vị trí của M.
Cho hình chữ nhật ABCD nội tiếp đường tròn tâm O. Trên cung nhỏ AB lấy điểm E ( E ko trùng A và B), F là giao của AB và CE.
a) CM tứ giác FBHE nội tiếp
b) CM \(\widehat{FHA}=\widehat{ADE}\) ???
Tính diện tích lớn nhất của hình chữ nhật ABCD nội tiếp trong nửa đường tròn có bán kính 10cm (hình vẽ) A.
160
c
m
2
B.
100
c
m
2
C.
80
c
m
2
D.
200
c
m
2
Đọc tiếp
Tính diện tích lớn nhất của hình chữ nhật ABCD nội tiếp trong nửa đường tròn có bán kính 10cm (hình vẽ)
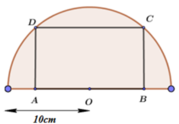
A. 160 c m 2
B. 100 c m 2
C. 80 c m 2
D. 200 c m 2
Tính diện tích lớn nhất của hình chữ nhật ABCD nội tiếp trong nửa đường tròn có bán kính 10cm (hình vẽ)
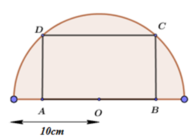
A. 160
B. 100
C. 80
D. 200
Cho hình chữ nhật ABCD nội tiếp (O).Tiếp tuyến tại C với đường tròn Cắt AB,AD lần lượt tại E,F.
a)Cm:AB.AE=AD.AF
b)Gọi M là trung điểm của EF.Cm:AM=BD
c)Đường tròn đường kính EF cắt (O) tại K,Ak cắt EF tại S.Cm:B,D,S thẳng hàng
mình không vẽ hình nhé
a) \(\Delta ABD~\Delta AFE\left(g.g\right)\Rightarrow\frac{AB}{AF}=\frac{AD}{AE}\Rightarrow AB.AE=AD.AF\)
b) AM cắt BD tại H
Xét \(\Delta AEF\)có M là trung điểm EF
\(\Rightarrow AM=MF=ME\)
\(\Rightarrow\Delta AMF\)cân tại M
\(\Rightarrow\widehat{MAF}=\widehat{MFA}=\widehat{ABD}\)
Mà \(\widehat{ABD}+\widehat{ADB}=90^o\Rightarrow\widehat{MAF}+\widehat{ADB}=90^o\)
\(\Rightarrow\widehat{AHD}=90^o\Rightarrow AM\perp BD\)
c) vì AK là dây chung của hai đường tròn ( O ) và ( M ) nên \(OM\perp AK\)
Xét \(\Delta AMS\)có MO và AO là đường cao nên O là trực tâm
\(\Rightarrow SO\perp AM\)( 1 )
Mà \(BD\perp AM\)( 2 )
Từ ( 1 ) và ( 2 ) nên B,D,S thẳng hàng


















