Cho A=\([\)0,3) và B={b,b+4}. Xác định b để A\(\subset\)B

Những câu hỏi liên quan
Xác định điều kiện của a,b để:
a, \(A\cap B\ne\varnothing\)với \(A=\left(a-1;a+2\right);B=(b;b+4]\)
b, \(E\subset\left(C\cup D\right)\) với \(C=\left[-1;4\right];D=R\backslash\left(-3;3\right);E=\left[a;b\right]\)
Cho A = { 1; 2; 3; 4; 5 } và B = { 3; 5 }
a) A có mấy tập hợp con, là những tập nào?
b) Hãy xác định 1 tập hợp C thỏa mãn \(B\subset C\)và \(C\subset A\). Có mấy tập C như vậy? Kể tên
a. A có 1 tập hợp con, gồm tập hợp con B
b.C={ 2; 3; 4; 5 } Có 2 tập hợp C như vậy, gồm C={2; 3; 4; 5} và C={1; 3; 4; 5}
ủng hộ mình nha!
Đúng 0
Bình luận (0)
[1] Cho hai tập hợp A = { 1; 2; 3; 4; 5 }; B = { 3; 4; 5 }. Biết B \(\subset A\), xác định tập hợp T = \(C_AB\)
A. T = { 1; 2; 3 } B. T = { 3; 4: 5 } C. T = { 1; 2 } D. T = { 1; 2; 3; 4; 5 }
Ta có:
Tập hợp A:
\(A=\left\{1;2;3;4;5\right\}\)
Tập hợp B:
\(B=\left\{3;4;5\right\}\)
Mà: \(B\subset A\) và \(T=C_AB\)
\(\Rightarrow T=\left\{1;2\right\}\)
⇒ Chọn C
Đúng 1
Bình luận (0)
[1] Cho tập hợp A = { 1; a; b }. Chọn khằng định sai:
A. \(\varnothing\subset A\) B. \(A\subset A\) C. \(1\subset A\) D. \(\left\{a;b\right\}\) \(\subset A\)
Ta có:
\(A=\left\{1;a;b\right\}\)
Xét:
A. \(\varnothing\subset A\) (đúng)
B. \(A\subset A\) (đúng)
C. \(1\subset A\) (sai)
D. \(\left\{a,b\right\}\subset A\) (đúng)
⇒ Chọn C
Đúng 2
Bình luận (0)
Xác định tính đúng sai của mỗi mệnh đề sau:
a) \(\{ a\} \in \{ a;b;c;d\} \)
b) \(\emptyset = \{ 0\} \)
c) \(\{ a;b;c;d\} \in \{ b;a;d;c\} \)
d) \(\{ a;b;c\} \not {\subset } \{ a;b;c\} \)
a) \(\{ a\} \in \{ a;b;c;d\} \) là mệnh đề sai, vì không có quan hệ \( \in \) giữa hai tập hợp.
b) \(\emptyset = \{ 0\} \) là mệnh đề sai, vì tập rỗng là tập không có phần tử nào, còn tập {0} có một phần tử là 0.
c) \(\{ a;b;c;d\} = \{ b;a;d;c\} \) là mệnh đề đúng (có thể thay đổi tùy ý vị trí các phần tử trong một tập hợp).
d) \(\{ a;b;c\} \not {\subset} \{ a;b;c\} \) là mệnh đề sai, vì mỗi phần tử a,b,c đều thuộc tập hợp \(\{ a;b;c\} \).
Đúng 0
Bình luận (0)
Bạn An khẳng định rằng: Với các tập hợp A, B, C bất kì, nếu \(A \subset B\) và \(B \subset C\) thì \(A \subset C.\)
Khẳng định của bạn An có đúng không? Hãy giải thích bằng cách sử dụng biểu đồ Ven.
Tham khảo:
+) Biểu diễn: \(A \subset B\)
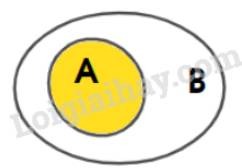
+) Sau đó, biểu diễn: \(B \subset C\)

Quan sát biểu đồ Ven, dễ thấy \(A \subset C.\)
Đúng 0
Bình luận (0)
Cho hai tập khác rỗng \(A=(m-1;4],B=\left(-2;2m+2\right)\) , với \(m\in R\). Xác định , để
a) \(A\cap B\ne\phi\)
b) \(A\subset B\)
c) \(B\subset A\)
d) \(\left(A\cap B\right)\subset\left(-1;3\right)\)
Cho A = [2 ; 4) ; B = ( - \(\infty\) ; m ]
a) Tìm m để A \(\cap\) B = \(\varnothing\)
b) Tìm m để A \(\cap\) B \(\ne\) \(\varnothing\)
c) Tìm m để A \(\subset\) B
*Cần gấp làm ơn giúp mình với*
\(A\cap B=\varnothing\Leftrightarrow m< 2\)
\(A\cap B\ne\varnothing\Leftrightarrow m\ge2\)
\(A\in B\Leftrightarrow m\ge4\)
Đúng 0
Bình luận (0)
Cho A =(5;+\(\infty\))
B= (2m+1;+\(\infty\))
Tìm m để a) A\(\subset\)B b) B\(\subset\)A
Giải hộ mk vs ạ< mk đang cần gấp, cảm ơn
a: Để A là tập con của B thì 2m+1<5
=>m<2
b: Để B là tập con của A thì 2m+1>5
=>m>2
Đúng 0
Bình luận (0)















