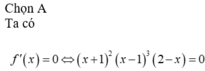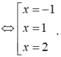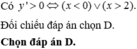cho hàm số f:R-R đồng biến và f(x+y)=f(x)+f(y).Tìm f(x)

Những câu hỏi liên quan
Tìm tất cả hàm số \(f:R\rightarrow R\) thỏa mãn\(f\left(f\left(x+y\right).f\left(x-y\right)\right)=x^2-y.f\left(y\right)\) \(\forall x,y\in R\)
Tìm tất cả hàm số \(f:R^+\rightarrow R^+\) thoả mãn:
\(f\left(x^2+y^2\right)=f\left(xy\right),\forall x,y\in R^+\)
Tìm tất cả hàm số \(f:R\rightarrow R\) thoả mãn:
\(f\left(xf\left(y\right)-y\right)+f\left(xy-x\right)+f\left(x+y\right)=2xy,\forall x,y\in R\)
Em chỉ mới chứng minh được f là hàm lẻ ạ, mong mọi người giúp :'(
Thay \(x=0;y=0\) vào giả thiết ta được \(f\left(0\right)=0\)
Thay \(y=0\) ta được \(f\left(x\right)+f\left(-x\right)=0\Rightarrow f\) là hàm lẻ
(Phân tích 1 chút: khi đã có hàm lẻ, ta cần thế tiếp 1 cặp sao cho "khử" được biểu thức phức tạp dạng hàm lồng đầu tiên, bằng cách tìm 1 giá trị y sao cho: \(x.f\left(y\right)-y=-\left(x+y\right)\) hoặc là \(x.f\left(y\right)-y=-\left(xy-x\right)\). Cái thứ nhất cho ta \(x.\left[f\left(y\right)+1\right]=0\Rightarrow f\left(y\right)=-1\) , nghĩa là ta chỉ cần tìm 1 hằng số c sao cho \(f\left(c\right)=-1\). Cái thứ 2 ko cho điều gì tốt nên bỏ qua. Bây giờ ta đi tìm c. Vế phải cần bằng -1, nghĩa là \(xy=-\dfrac{1}{2}\), vế trái cần khử bớt 2 số hạng. Nhưng trước khi có c thì \(f\left(x.f\left(y\right)-y\right)\) chưa khử được, nên ta cần khử cặp sau, bằng cách cho \(xy-x=-\left(x+y\right)\Rightarrow xy=-y\Rightarrow x=-1\), thay vào \(xy=-\dfrac{1}{2}\Rightarrow y=\dfrac{1}{2}\). Xong.)
Thế \(x=-1;y=\dfrac{1}{2}\) ta được:
\(f\left(-f\left(\dfrac{1}{2}\right)-\dfrac{1}{2}\right)+f\left(-\dfrac{1}{2}+1\right)+f\left(-1+\dfrac{1}{2}\right)=-1\)
\(\Leftrightarrow f\left(-f\left(\dfrac{1}{2}\right)-\dfrac{1}{2}\right)=-1\)
Đặt \(c=-f\left(\dfrac{1}{2}\right)-\dfrac{1}{2}\) là 1 hằng số nào đó
\(\Rightarrow f\left(c\right)=-1\)
Thế \(y=c\) vào ta được:
\(f\left(x.f\left(c\right)-c\right)+f\left(cx-x\right)+f\left(x+c\right)=2c.x\)
\(\Leftrightarrow f\left(-x-c\right)+f\left(x+c\right)+f\left(cx-x\right)=2c.x\)
\(\Leftrightarrow f\left(cx-x\right)=2c.x\) (1)
- Nếu \(c=1\Rightarrow f\left(0\right)=2x\) ko thỏa mãn \(f\left(0\right)=0\)
\(\Rightarrow c\ne1\), khi đó đặt \(cx-x=t\) \(\Rightarrow x=\dfrac{t}{c-1}\)
(1) trở thành \(f\left(t\right)=\dfrac{2c}{c-1}.t\)
Đặt \(\dfrac{2c}{c-1}=a\) \(\Rightarrow f\left(t\right)=a.t\)
Hay hàm cần tìm có dạng \(f\left(x\right)=ax\) với a là hằng số
Đúng 3
Bình luận (2)
Cho hàm số y f(x) liên tục trên R và có
f
(
x
)
x
+
1
2
x
-
1
3
2
-
x
. Hàm số y f(x) đồng biến trên...
Đọc tiếp
Cho hàm số y = f(x) liên tục trên R và có f ' ( x ) = x + 1 2 x - 1 3 2 - x . Hàm số y = f(x) đồng biến trên khoảng nào dưới đây?
A. ![]() .
.
B. ![]() .
.
C. ![]() .
.
D. ![]() .
.
Cho hàm số y f(x) có đạo hàm trên R và có đồ thị hàm số y f(x) như hình bên. Hàm số y f (3-x) đồng biến trên khoảng nào dưới đây? A. B. C. D.
Đọc tiếp
Cho hàm số y = f(x) có đạo hàm trên R và có đồ thị hàm số y = f'(x) như hình bên. Hàm số y= f (3-x) đồng biến trên khoảng nào dưới đây?
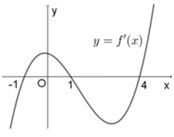
A. ![]()
B. ![]()
C. ![]()
D. ![]()
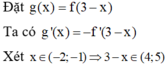
![]()
=> hàm số y=g(x) nghịch biến trên (-2; -1)
![]()
![]()
=>hàm số y=g(x) đồng biến trên (-1;2)
Chọn B
Đúng 0
Bình luận (0)
Cho hàm số y f(x) có đạo hàm trên R và có đồ thị hàm số yf(x) như hình bên. Hàm số yf(3-x) đồng biến trên khoảng nào dưới đây?
Đọc tiếp
Cho hàm số y = f(x) có đạo hàm trên R và có đồ thị hàm số y=f'(x) như hình bên. Hàm số y=f(3-x) đồng biến trên khoảng nào dưới đây?
![]()
![]()
![]()
![]()
Câu 5. Cho hàm số f x có đạo hàm liên tục tên R và có đạo hàm ' 2 f x x x 9 1 .Tìm m để hàm số 2 y f x x m 2 đồng biến trên 1,3
Cho hàm số
y
f
(
x
)
liên tục trên R và có đạo hàm
f
(
x
)
(
1
-
x
)
2
(
x
+
1
)
3
(
3
-
x
)
. Hàm số
y
f
(
x
)
đồng biến trên khoảng nào dưới đây
Đọc tiếp
Cho hàm số y = f ( x ) liên tục trên R và có đạo hàm f ' ( x ) = ( 1 - x ) 2 ( x + 1 ) 3 ( 3 - x ) . Hàm số y = f ( x ) đồng biến trên khoảng nào dưới đây
![]()
![]()
![]()
![]()
Cho hàm số yf(x) liên tục trên R và có bảng xét dấu của hàm số f(x) như sau:Hàm số yf(x) đồng biến trên khoảng nào dưới đây ? A.(0;2) B.
1
;
+
∞
C.
0
;
+
∞
D.
-
∞
;...
Đọc tiếp
Cho hàm số y=f(x) liên tục trên R và có bảng xét dấu của hàm số f'(x) như sau:

Hàm số y=f(x) đồng biến trên khoảng nào dưới đây ?
A.(0;2)
B. 1 ; + ∞
C. 0 ; + ∞
D. - ∞ ; 0