Thực hiện phép tính (làm chi tiết cho mik hiểu ạ=((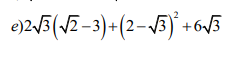

Những câu hỏi liên quan
Thực hiện phép tính (làm chi tiết cho mik hiểu ạ=((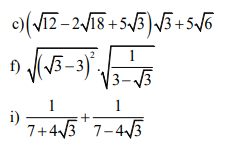
\(c,=\left(2\sqrt{3}-6\sqrt{2}+5\sqrt{3}\right)\sqrt{3}+5\sqrt{6}\\ =\left(7\sqrt{3}-6\sqrt{2}\right)\sqrt{3}+5\sqrt{6}\\ =21-6\sqrt{6}+5\sqrt{6}=21-\sqrt{6}\\ f,=\sqrt{\dfrac{\left(\sqrt{3}-3\right)^2}{3-\sqrt{3}}}=\sqrt{\dfrac{\left(3-\sqrt{3}\right)^2}{3-\sqrt{3}}}=\sqrt{3-\sqrt{3}}\\ i,=\dfrac{7-4\sqrt{3}+7+4\sqrt{3}}{7^2-\left(4\sqrt{3}\right)^2}=\dfrac{14}{49-48}=\dfrac{14}{1}=14\)
Đúng 3
Bình luận (0)
THỰC HIỆN PHÉP TÍNH (LÀM CHI TIẾT)
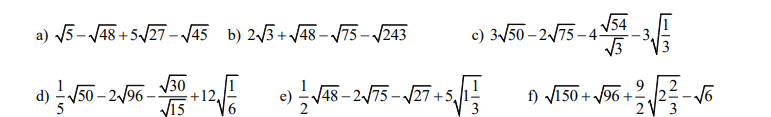
Chủ yếu em phân tích sao cho có nhân tử chung ra là được
Đúng 0
Bình luận (0)
a) \(\sqrt{5}-\sqrt{48}+5\sqrt{27}-\sqrt{45}=\sqrt{5}-\sqrt{16.3}+5\sqrt{9.3}-\sqrt{9.5}\)
\(=\sqrt{5}-4\sqrt{3}+15\sqrt{3}-3\sqrt{5}=11\sqrt{3}-2\sqrt{5}\)
b) \(2\sqrt{3}+\sqrt{48}-\sqrt{75}-\sqrt{243}=2\sqrt{3}+\sqrt{16.3}-\sqrt{25.3}-\sqrt{81.3}\)
\(=2\sqrt{3}+4\sqrt{3}-5\sqrt{3}-9\sqrt{3}=-8\sqrt{3}\)
c) \(3\sqrt{50}-2\sqrt{75}-4\dfrac{\sqrt{54}}{\sqrt{3}}-3\sqrt{\dfrac{1}{3}}\)
\(=3\sqrt{25.2}-2\sqrt{25.3}-4\sqrt{\dfrac{54}{3}}-\sqrt{9.\dfrac{1}{3}}=15\sqrt{2}-10\sqrt{3}-4\sqrt{18}-\sqrt{3}\)
\(=15\sqrt{2}-11\sqrt{3}-4\sqrt{9.2}=15\sqrt{2}-11\sqrt{3}-12\sqrt{2}=3\sqrt{2}-11\sqrt{3}\)
mấy câu dưới bạn làm tương tự thôi
Đúng 0
Bình luận (0)
d) Ta có: \(\dfrac{1}{5}\sqrt{50}-2\sqrt{96}-\dfrac{\sqrt{30}}{\sqrt{15}}+12\sqrt{\dfrac{1}{6}}\)
\(=\dfrac{1}{5}\cdot5\sqrt{2}-2\cdot4\sqrt{6}-\sqrt{2}+\dfrac{12}{\sqrt{6}}\)
\(=\sqrt{2}-\sqrt{2}+2\sqrt{6}-8\sqrt{6}\)
\(=-6\sqrt{6}\)
e) Ta có: \(\dfrac{1}{2}\sqrt{48}-2\sqrt{75}-\sqrt{27}+5\sqrt{1\dfrac{1}{3}}\)
\(=\dfrac{1}{2}\cdot4\sqrt{3}-2\cdot5\sqrt{3}-3\sqrt{3}+5\cdot\dfrac{2}{\sqrt{3}}\)
\(=2\sqrt{3}-10\sqrt{3}-3\sqrt{3}+\dfrac{10\sqrt{3}}{3}\)
\(=-11\sqrt{3}+\dfrac{10\sqrt{3}}{3}\)
\(=\dfrac{-33+10\sqrt{3}}{3}\)
f) Ta có: \(\sqrt{150}+\sqrt{96}+\dfrac{9}{2}\cdot\sqrt{2\dfrac{2}{3}}-\sqrt{6}\)
\(=5\sqrt{6}+4\sqrt{6}+\dfrac{9}{2}\cdot\sqrt{\dfrac{8}{3}}-\sqrt{6}\)
\(=8\sqrt{6}+\dfrac{9}{2}\cdot\dfrac{2\sqrt{2}}{\sqrt{3}}\)
\(=8\sqrt{6}+3\sqrt{6}\)
\(=11\sqrt{6}\)
Đúng 0
Bình luận (0)
THỰC HIỆN PHÉP TÍNH ( LÀM CHI TIẾT)
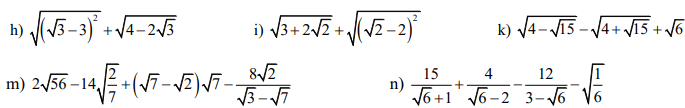
n)\(\dfrac{15}{\sqrt{6}+1}+\dfrac{4}{\sqrt{6}-2}-\dfrac{12}{3-\sqrt{6}}-\sqrt{\dfrac{1}{6}}\)
=\(\dfrac{15\left(\sqrt{6}-1\right)}{\left(\sqrt{6}+1\right)\left(\sqrt{6}-1\right)}+\dfrac{4\left(\sqrt{6}+2\right)}{\left(\sqrt{6}-2\right)\left(\sqrt{6}+2\right)}-\dfrac{12\left(3+\sqrt{6}\right)}{\left(3-\sqrt{6}\right)\left(3+\sqrt{6}\right)}-\sqrt{\dfrac{1}{6}}\)
=\(\dfrac{15\left(\sqrt{6}-1\right)}{5}+\dfrac{4\left(\sqrt{6}+2\right)}{2}-\dfrac{12\left(3+\sqrt{6}\right)}{3}-\sqrt{\dfrac{1}{6}}\)
=\(3\left(\sqrt{6}-1\right)+2\left(\sqrt{6}+2\right)-4\left(3+\sqrt{6}\right)-\sqrt{\dfrac{1}{6}}\)
=\(3\sqrt{6}-3+2\sqrt{6}+4-12-4\sqrt{6}-\sqrt{\dfrac{1}{6}}\)
=\(\sqrt{6}-11-\sqrt{\dfrac{1}{6}}\)
=\(\dfrac{5-11\sqrt{6}}{\sqrt{6}}\)
Đúng 1
Bình luận (0)
h)\(\sqrt{\left(\sqrt{3}-3\right)^2}+\sqrt{4-2\sqrt{3}}\)
=\(\left|\sqrt{3}-3\right|+\sqrt{3-2\sqrt{3}+1}\)
=\(3-\sqrt{3}+\sqrt{\left(\sqrt{3}-1\right)^2}\)
=\(3-\sqrt{3}+\left|\sqrt{3}-1\right|\)
=\(3-\sqrt{3}+\sqrt{3}-1\)
=2
Đúng 0
Bình luận (0)
THỰC HIỆN PHÉP TÍNH (LÀM CHI TIẾT)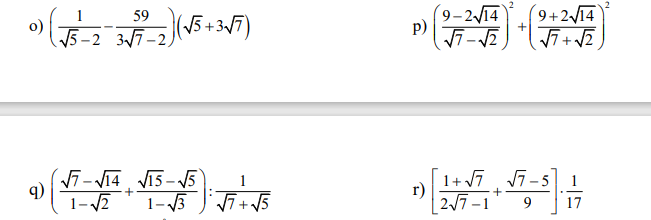
o) Ta có: \(\left(\dfrac{1}{\sqrt{5}-2}-\dfrac{59}{3\sqrt{7}-2}\right)\left(\sqrt{5}+3\sqrt{7}\right)\)
\(=\left(\sqrt{5}+2-3\sqrt{7}-2\right)\left(\sqrt{5}+3\sqrt{7}\right)\)
\(=\left(\sqrt{5}-3\sqrt{7}\right)\left(\sqrt{5}+3\sqrt{7}\right)\)
=5-63=-58
p) Ta có: \(\left(\dfrac{9-2\sqrt{14}}{\sqrt{7}-\sqrt{2}}\right)^2+\left(\dfrac{9+2\sqrt{14}}{\sqrt{7}+\sqrt{2}}\right)^2\)
\(=\left(\sqrt{7}-\sqrt{2}\right)^2+\left(\sqrt{7}+\sqrt{2}\right)^2\)
\(=9-2\sqrt{14}+9+2\sqrt{14}\)
=18
q) Ta có: \(\left(\dfrac{\sqrt{7}-\sqrt{14}}{1-\sqrt{2}}+\dfrac{\sqrt{15}-\sqrt{5}}{1-\sqrt{3}}\right):\dfrac{1}{\sqrt{7}+\sqrt{5}}\)
\(=\left(\sqrt{7}-\sqrt{5}\right)\cdot\left(\sqrt{7}+\sqrt{5}\right)\)
=7-5=2
Đúng 1
Bình luận (0)
bài1.Thực hiện phép tính(tính hợp lí nếu có thể)
a,\(4\frac{1}{5}-\frac{1}{5}.\frac{10}{11}+15\%\)
CÁc bn làm chi tiết hộ mik nhé sáng mai mik nộp rồi ai làm đúng mik tick cho
Thực hiện phép tính (làm chi tiết):
3) \(\sqrt{8-3\sqrt{7}}+\sqrt{4-\sqrt{7}}\)
Lời giải:
\(A=\sqrt{8-3\sqrt{7}}+\sqrt{4-\sqrt{7}}\)
$A\sqrt{2}=\sqrt{16-6\sqrt{7}}+\sqrt{8-2\sqrt{7}}$
$=\sqrt{(3-\sqrt{7})^2}+\sqrt{(\sqrt{7}-1)^2}$
$=|3-\sqrt{7}|+|\sqrt{7}-1|$
$=3-\sqrt{7}+\sqrt{7}-1=2$
Đúng 1
Bình luận (0)
Thực hiện phép chia:( chi tiết cho mình nhed, mình cảm ơn ạ)
Ta có:
A(x)= 6x3 - 7x2 - x + m; B(x)= 2x + 1
Hãy thực hiện phép chia A(x) cho B(x).
\(\dfrac{A}{B}=\dfrac{6x^3+3x^2-10x^2-5x+4x+2+m-2}{2x+1}\)
\(=3x^2-5x+2+\dfrac{m-2}{2x+1}\)
Đúng 0
Bình luận (0)
Thực hiện phép tính (làm chi tiết):
\(\left(\sqrt{10}-\sqrt{2}\right)\sqrt{4+\sqrt{6-2\sqrt{5}}}\)
\(\left(\sqrt{10}-\sqrt{2}\right)\sqrt{4+\sqrt{6-2\sqrt{5}}}\\ =\left(\sqrt{10}-\sqrt{2}\right)\sqrt{4+\sqrt{\left(\sqrt{5}-1\right)^2}}\\ =\left(\sqrt{10}-\sqrt{2}\right)\sqrt{3+\sqrt{5}}\\ =\sqrt{10}\cdot\sqrt{3+\sqrt{5}}-\sqrt{2}\cdot\sqrt{3+\sqrt{5}}\\ =\sqrt{30+10\sqrt{5}}-\sqrt{6+2\sqrt{5}}\\ =\sqrt{\left(5+\sqrt{5}\right)^2}-\sqrt{\left(\sqrt{5}+1\right)^2}\\ =5+\sqrt{5}-\sqrt{5}-1\\ =4\)
Đúng 3
Bình luận (0)
Cho mình hỏi phép tính 20000-20% thực hiện giải chi tiết như nào

















