Đặt \(x^3=a,y^3=b,z^3=c\Rightarrow abc=1\)

\(P=\dfrac{a^3+b^3}{a^2+ab+b^2}+\dfrac{b^3+c^3}{b^2+bc+c^2}+\dfrac{c^3+a^3}{c^2+ca+a^2}\)

Ta chứng minh bổ đề sau

\(\dfrac{a^3+b^3}{a^2+ab+b^2}\ge\dfrac{a+b}{3}\)

\(\Leftrightarrow3\left(a^3+b^3\right)\ge\left(a+b\right)\left(a^2+ab+b^2\right)\)

\(\Leftrightarrow3\left(a^3+b^3\right)\ge a^3+2ab^2+2a^2b+b^3\)

\(\Leftrightarrow a^3+b^3\ge ab\left(a+b\right)\)

\(\Leftrightarrow\left(a+b\right)\left(a-b\right)^2\ge0\)

Bất đẳng thức cuối luôn đúng. Sử dụng bổ đề ta được

\(P\ge\dfrac{a+b}{3}+\dfrac{b+c}{3}+\dfrac{c+a}{3}=\dfrac{2\left(a+b+c\right)}{3}\ge\dfrac{2.3\sqrt[3]{abc}}{3}=2\)

1: (x+1)(y+2)=5

mà y+2>=2(do y là số tự nhiên)

nên (x+1;y+2)∈(1;5)

=>(x;y)∈(0;3)

2: (x+1)(y+2)=6

mà x+1>=1 và y+2>=2(do x,y là các số tự nhiên)

nên (x+1;y+2)∈{(3;2);(2;3);(1;6)}

=>(x;y)∈{(2;0);(1;1);(0;4)}

3: (x+2)(y+3)=6

mà x+2>=2 và y+3>=3(do x,y là các số tự nhiên)

nên (x+2;y+3)∈{(2;3)}

=>(x;y)∈(0;0)

4: (x-1)(y+3)=6

mà y+3>=3(do y là số tự nhiên)

nên (x-1;y+3)∈{(2;3);(1;6)}

=>(x;y)∈{(3;0);(2;3)}

5: (x-1)(y-3)=5

=>(x-1;y-3)∈{(1;5);(5;1)}

=>(x;y)∈{(4;8);(6;4)}

6: (x-2)(y-1)=3

=>(x-2;y-1)∈{(1;3);(3;1)}

=>(x;y)∈{(3;4);(5;2)}

7: (x-2)(y-1)=5

=>(x-2;y-1)∈{(1;5);(5;1)}

=>(x;y)∈{(3;6);(7;2)}

8: (x-3)(y+1)=7

mà y+1>=1(do y là số tự nhiên)

nên (x-3;y+1)∈{(1;7);(7;1)}

=>(x;y)∈{(4;6);(10;0)}

cầu giúp đỡ ,mik còn nhiều lắm T_T

Áp dụng tính chất của dãy tỉ số bằng nhau ta có:

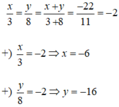
Chọn (B) x = -6; y = -16.

Vì chia hết cho 5 

\(\Rightarrow y=0\) hoặc \(y=5\)

\(Th1:y=0\\ \Rightarrow x-0=6\\\Rightarrow x=6\)           \(\Rightarrow x=6;y=0\)

\(Th2:y=5\\ \Rightarrow x-5=6\\ \Rightarrow x=11\)           \(\Rightarrow x=11;y=5\)

\(\Rightarrow A\)