tìm x,y,z biết 4x2+y2+z2-4x+2y+2=0. giải nhanh giúp mình với huhu

Những câu hỏi liên quan
tìm x,y,z biết 4x2+y2+z2-4x+2y+2=0. giải nhanh giúp mình với huhu
c) C x(y2 +z2)+y(z2 +x2)+z(x2 +y2)+2xyz.
d) D x3(y−z)+y3(z−x)+z3(x−y).
e) E (x+y)(x2 −y2)+(y+z)(y2 −z2)+(z+x)(z2 −x2).
b) x2 +2x−24 0.
d) 3x(x+4)−x2 −4x 0.
f) (x−1)(x−3)(x+5)(x+7)−297 0.
(2x−1)2 −(x+3)2 0.
c) x3 −x2 +x+3 0.
e) (x2 +x+1)(x2 +x)−2 0.
a) A x2(y−2z)+y2(z−x)+2z2(x−y)+xyz.
b) B x(y3 +z3)+y(z3 +x3)+z(x3 +y3)+xyz(x+y+z). c) C x(y2 −z2)−y(z2 −x2)+z(x2 −y2).
Đọc tiếp
c) C = x(y2 +z2)+y(z2 +x2)+z(x2 +y2)+2xyz.
d) D = x3(y−z)+y3(z−x)+z3(x−y).
e) E = (x+y)(x2 −y2)+(y+z)(y2 −z2)+(z+x)(z2 −x2).
b) x2 +2x−24 = 0.
d) 3x(x+4)−x2 −4x = 0.
f) (x−1)(x−3)(x+5)(x+7)−297 = 0.
(2x−1)2 −(x+3)2 = 0.
c) x3 −x2 +x+3 = 0.
e) (x2 +x+1)(x2 +x)−2 = 0.
a) A = x2(y−2z)+y2(z−x)+2z2(x−y)+xyz.
b) B = x(y3 +z3)+y(z3 +x3)+z(x3 +y3)+xyz(x+y+z). c) C = x(y2 −z2)−y(z2 −x2)+z(x2 −y2).
Đề bài yêu cầu gì vậy em.
Đúng 0
Bình luận (0)
tìm ba số x , y , z biết 3x2 - y2 + z2= 876 , x và y tỉ lệ nghịch với 3 và 2 , y và z tỉ lệ nghịch với 4 và 5
giúp mình với mình cần gấp lắm
Lời giải:
Theo bài ra ta có:
$3x=2y; 4y=5z$
$\Rightarrow \frac{x}{2}=\frac{y}{3}; \frac{y}{5}=\frac{z}{4}$
$\Rightarrow \frac{x}{10}=\frac{y}{15}=\frac{z}{12}$
Đặt $\frac{x}{10}=\frac{y}{15}=\frac{z}{12}=k$
$\Rightarrow x=10k; y=15k; z=12k$
Khi đó:
$3x^2-y^2+z^2=876$
$\Rightarrow 3(10k)^2-(15k)^2+(12k)^2=876$
$\Rightarrow 219k^2=876$
$\Rightarrow k^2=4$
$\Rightarrow k=\pm 2$
Nếu $k=2$ thì $x=10k=20; y=15k=30; z=12k=24$
Nếu $k=-2$ thì $x=10k=-20; y=15k=-30; z=12k=-24$
Đúng 0
Bình luận (0)
Giúp mình giải bài này nha
Cho x, y, z ≠0 và (y2+z2−x2)/2yz +(z2+x2−y2)/2xz +
(x2+y2−z2)/2xy =1. Chứng minh rằng trong ba phân thức đã cho có một phân thức bằng 1 và một phân thức bằng -1.
Nhanh lên nhé Mình cần gấp lắm😢
Trong không gian với hệ trục tọa độ Oxyz cho hai mặt cầu:
(
S
1
)
:
x
2
+
y
2
+
z
2
+
4
x
+
2
y
+
z
0
;
(
S
2
)
;
x
2...
Đọc tiếp
Trong không gian với hệ trục tọa độ Oxyz cho hai mặt cầu:
( S 1 ) : x 2 + y 2 + z 2 + 4 x + 2 y + z = 0 ;
( S 2 ) ; x 2 + y 2 + z 2 - 2 x - y - z = 0
cắt nhau theo một đường tròn (C) nằm trong mặt phẳng (P). Cho các điểm A (1; 0; 0), B (0; 2; 0), C (0; 0; 3). Có bao nhiêu mặt cầu tâm thuộc (P) và tiếp xúc với cả ba đường thẳng AB, BC, CA?
A. 4 Mặt cầu.
B. 2 Mặt cầu.
C. 3 Mặt cầu.
D. 1 Mặt cầu.
Chọn A
Mặt phẳng (P) chứa đường tròn (C) (giao của 2 mặt cầu đã cho) có phương trình là: 6x + 3y + 2z = 0
Mặt phẳng (P) có phương trình là:
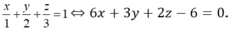
Do đó (P) // (ABC). Mặt cầu (S) tiếp xúc với cả ba đường thẳng AB, BC, CA sẽ giao với mặt phẳng (ABC) theo một đường tròn tiếp xúc với ba đường thẳng AB, BC, CA.
Trên mặt phẳng (ABC) có 4 đường tròn tiếp xúc với ba đường thẳng AB, BC, CA đó là đường tròn nội tiếp tam giác ABC và ba đường tròn bàng tiếp các góc A, B, C. Do đó có 4 mặt cầu có tâm nằm trên (P) và tiếp xúc với cả ba đường thẳng AB, BC, CA. Tâm của 4 mặt cầu là hình chiếu của tâm 4 đường tròn tiếp xúc với ba đường thẳng AB, BC, CA lên mặt phẳng (P).
Đúng 0
Bình luận (0)
Trong không gian với hệ toạ độ Oxyz, cho mặt cầu (S):
x
2
+
y
2
+
z
2
+
4
x
-
6
y
+
m
0
và đường thẳng (d) là giao tuyến của 2 mặt phẳng (P):
2
x
-
2
y
-
z
+
1
0
, (Q):
x
+
2
y
-
2
z
-
4
0
....
Đọc tiếp
Trong không gian với hệ toạ độ Oxyz, cho mặt cầu (S): x 2 + y 2 + z 2 + 4 x - 6 y + m = 0 và đường thẳng (d) là giao tuyến của 2 mặt phẳng (P): 2 x - 2 y - z + 1 = 0 , (Q): x + 2 y - 2 z - 4 = 0 . Tìm m để (S) cắt (d) tại 2 điểm M, N sao cho độ dài MN = 8.
A. m = 2
B. m = -12
C. m = 12
D. m = -2
Trong không gian với hệ toạ độ Oxyz, cho mặt cầu (S):
x
2
+
y
2
+
z
2
+
4
x
-
6
y
+
m
0
và đường thẳng (d) là giao tuyến của 2 mặt phẳng (P):
2
x
-
2
y
-
z
+
1
0
, (Q):
x
+
2
y
-
2
z
-
4
0
....
Đọc tiếp
Trong không gian với hệ toạ độ Oxyz, cho mặt cầu (S): x 2 + y 2 + z 2 + 4 x - 6 y + m = 0 và đường thẳng (d) là giao tuyến của 2 mặt phẳng (P): 2 x - 2 y - z + 1 = 0 , (Q): x + 2 y - 2 z - 4 = 0 . Tìm m để (S) cắt (d) tại 2 điểm M, N sao cho độ dài MN = 8.
A. m = 2
B. m = -12
C. m = 12
D. m = -2
Mình đang cần gấp! Giúp mình với ạ
Bài 3: Chứng minh rằng:
a) (x+y+z)2= x2+y2+z2+2xy+2xz+2yz
b) (x-y).(x2+y2+z2-xy-yz-xz)= x3+y3+z3-3xyz
c) (x+y+z)3= x3+y3+z3+3.(x+y).(y+z).(z+x)
Bài 3:
a, (\(x\)+y+z)2
=((\(x\)+y) +z)2
= (\(x\) + y)2 + 2(\(x\) + y)z + z2
= \(x^2\) + 2\(xy\) + y2 + 2\(xz\) + 2yz + z2
=\(x^2\) + y2 + z2 + 2\(xy\) + 2\(xz\) + 2yz
Đúng 1
Bình luận (0)
b, (\(x-y\))(\(x^2\) + y2 + z2 - \(xy\) - yz - \(xz\))
= \(x^3\) + \(xy^2\) + \(xz^2\) - \(x^2\)y - \(xyz\) - \(x^2\)z - y3
Đến dây ta thấy xuất hiện \(x^3\) - y3 khác với đề bài, em xem lại đề bài nhé
Đúng 1
Bình luận (0)
c,
(\(x\) + y + z)3
=(\(x\) + y)3 + 3(\(x\) + y)2z + 3(\(x\)+y)z2 + z3
= \(x^3\) + 3\(x^2\)y + 3\(xy^{2^{ }}\) + y3 + 3(\(x\)+y)z(\(x\) + y + z) + z3
= \(x^3\) + y3 + z3 + 3\(xy\)(\(x\) + y) + 3(\(x+y\))z(\(x+y+z\))
= \(x^3\) + y3 + z3 + 3(\(x\) + y)( \(xy\) + z\(x\) + yz + z2)
= \(x^3\) + y3 + z3 + 3(\(x\) + y){(\(xy+xz\)) + (yz + z2)}
= \(x^3\) + y3 + z3 + 3(\(x\) + y){ \(x\)( y +z) + z(y+z)}
= \(x^3\) + y3 + z3 + 3(\(x\) + y)(y+z)(\(x+z\)) (đpcm)
Đúng 0
Bình luận (0)
Tìm các bộ số tự nhiên ( x , y ,z ) thỏa mãn x \(\le\) y \(\le\) z; x2+y2+z2=34. ( Ai giúp mình với )
Dùng phương pháp chặn :
x \(\le\) y \(\le\) z \(\Rightarrow\) x2 \(\le\) y2 \(\le\) z2 \(\Rightarrow\) x2 + y2 + z2 \(\le\) 3z2
\(\Rightarrow\) 3z2 \(\ge\) 34 \(\Leftrightarrow\) z2 \(\ge\) 34/3 (1)
x2 + y2 + z2 = 34 mà x,y,z \(\in\) N \(\Rightarrow\) z2 \(\le\) 34 (2)
Kết hợp (1) và (2) ta có :
34/3 \(\le\) z2 \(\le\) 34
\(\Rightarrow\) z2 \(\in\) { 16; 25}
vì z \(\in\) N\(\Rightarrow\) z \(\in\) { 4; 5}
th1 Z = 4 ta có :
x2 + y2 + 16 = 34
x2 + y2 = 12
x \(\le\) y \(\Rightarrow\) x2 \(\le\)y2 \(\Rightarrow\) x2 + y2 \(\le\) 2y2 \(\Rightarrow\) 12 \(\le\)2y2 \(\Rightarrow\) y2 \(\ge\) 6 (*)
x2 + y2 = 12 \(\Rightarrow\) y2 \(\le\) 12 (**)
Kết hợp (*) và (**) ta có :
6 \(\le\) y2 \(\le\) 12 \(\Rightarrow\) y2 = 9 vì y \(\in\) N\(\Rightarrow\) y = 3
với y = 3 ta có : x2 + 32 = 12 \(\Rightarrow\) x2 = 12-9 = 3 \(\Rightarrow\) x = +- \(\sqrt{3}\)(loại vì x \(\in\) N)
th2 : z = 5 ta có :
x2 + y2 + 25 = 34
\(\Rightarrow\) x2 + y2 = 34 - 25 = 9
x \(\le\) y \(\Rightarrow\) x2 \(\le\) y2 \(\Rightarrow\) x2 + y2 \(\le\)2y2 \(\Rightarrow\) 2y2 \(\ge\) 9 \(\Rightarrow\) y2 \(\ge\) 9/2 (a)
x2 + y2 = 9 \(\Rightarrow\) y2 \(\le\) 9 (b)
Kết hợp (a) và (b) ta có :
9/2 \(\le\) y2 \(\le\) 9 \(\Rightarrow\) y2 = 9 vì y \(\in\) N \(\Rightarrow\) y = 3
với y = 3 \(\Rightarrow\) x2 + 32 = 9 \(\Rightarrow\) x2 = 0 \(\Rightarrow\) x = 0
kết luận (x; y; z) =( 0; 3; 5) là nghiệm duy nhất thỏa mãn pt
Đúng 2
Bình luận (0)














