cho da thuc
A=8x+1-8x3-10x2+3x4
B=3x2-2x+1
viet A voi dang A=B.Q+R
i) (3xy3− 12x2y2+ 6xy)2:3xy − xy
j) (10x3− 19x2-4x + 4): (2x + 1)
k) (3x4− 8x3-10x2+ 8x − 5): (3x2− 2x + 1).
j: \(\dfrac{10x^3-19x^2-4x+4}{2x+1}\)
\(=\dfrac{10x^3+5x^2-24x^2-12x+8x+4}{2x+1}\)
\(=5x^2-12x+4\)
cho hai da thuc A=x2-3x+8 va B=x-2 . tim du R trong phep chia A cho B roi viet duoi dang A=B.Q+R
Tại x = 2 thì giá trị đa thức A = 22 - 3 . 2 + 8 = 6
Theo định lý Bézout thì A chia B dư 6
Ta có: x2 - 3x + 8 = (x - 2).Q + 6
\(\Rightarrow\)x2 - 3x + 8 - 6 = (x - 2).Q
\(\Rightarrow\)x2 - 3x + 2 = (x - 2).Q
\(\Rightarrow\)Q = (x2 - 3x + 2) : (x - 2)
\(\Rightarrow\)Q = (x - 1)(x - 2) : (x - 2) = x - 1
Vậy A = B.(x - 1) + 6
a)Cho vi du ve 1 don thuc ,1 da thuc nhung khong phai la don thuc ,2 don thuc dong dang voi nhau ,da thuc 1 bien
b)Hay viet 1 don thuc dong dang voi don thuc don thuc xy\(^3\) sao cho tai x=-1 y=2 gia tri cua don thuc do la so nguyen duong nho hon 10
a) 5 ; x+y ;2xy đồng dạng với 4xy ;a (x) = 25x + 2x2
b) -2xy
a) cho vi du ve 1 don thuc ,1 da thuc nhung k phai la don thuc , 2 don thuc dong dang voi nhau .da thuc 1 bien
b) Hay viet 1 don thuc dong dang voi don thuc xy\(^3\) sao cho tai x=-1 y=2 gia tri cua don thuc do la so nguyen duong nho hon 10
GIUP MINH NHA
ko bt minh cung dang giai bai tuong tu do ne
a) Cho vidu ve 1 don thuc ,moi da thuc nhung k phai la don thuc 2 don thuc dong dang voi nhau,da thuc 1 bien
b) Hay viet 1 don thuc dong dang voi don thuc xy\(^3\) sao cho tai x=-1 y=2 gia tri cua don thuc do la so nguyen duong nho hon 10
CAC BAN GIUP MINH NHA MINH GAP LAM
cho da thuc P = 3x2-4y2+x.y+x+1
Hay viet P duoi dang tong cua mot da thuc voi da thuc 2x2-y2-xy
tinh ade da thuc 3x^3 + 2x^2 - 7x - a chia het cho da thuc 3x - 1 lam danh danh dang can gap
de f(x) chia het cho 3x - 1 thi f(1)=0
<=> 3.(1)^3 + 2.(1)^2 - 7.1 - a = 0
<=> 3 + 2 - 7 - a = 0
<=> -2 - a = 0
<=> a = -2
Viet cac da thuc sau duoi dang tich :
a, 100x2−(x2+25)2
b, 1+(x−y+5)2−2(x−y+5)
c, (x2+4y2−5)2−16(x2y2+2xy+1)
d, (x2+8x−34)2−(3x2−8x−2)2
a) \(100x^2-\left(x^2+25\right)^2\)
\(=\left(10x\right)^2-\left(x^2+25\right)^2\)
\(=\left(10x+x^2+25\right)\left(10x-x^2-25\right)\)
\(=\left(x+5\right)^2\left(10x-x^2-25\right)\)
b) \(1+\left(x-y+5\right)^2-2\left(x-y+5\right)\)
\(=\left[\left(x-y+5\right)-1\right]^2\)
\(=\left(x-y+4\right)^2\)
c) \(\left(x^2+4y^2-5\right)^2-16\left(x^2y^2+2xy+1\right)\)
\(=\left(x^2+4y^2-5\right)^2-4^2\left(xy+1\right)^2\)
\(=\left[\left(x^2+4y^2-5\right)-4\left(xy+1\right)\right]\left[\left(x^2+4y^2-5\right)+4\left(xy+1\right)\right]\)
\(=\left(x^2+4y^2-5-4xy-4\right)\left(x^2+4y^2-5+4xy+4\right)\)
\(=\left(x^2-4xy+4y^2-9\right)\left(x^2+4xy+4y^2-1\right)\)
\(=\left[\left(x-2y\right)^2-3^2\right]\left[\left(x+2y\right)^2-1^2\right]\)
\(=\left(x-2y-3\right)\left(x-2y+3\right)\left(x+2y-1\right)\left(x+2y+1\right)\)
d) \(\left(x^2+8x-34\right)^2-\left(3x^2-8x-2\right)^2\)
\(=\left[\left(x^2+8x-34\right)-\left(3x^2-8x-2\right)\right]\left[\left(x^2+8x-34\right)+\left(3x^2-8x-2\right)\right]\)
\(=\left(x^2+8x-34-3x^2+8x+2\right)\left(x^2+8x-34+3x^2-8x-2\right)\)
\(=\left(-2x^2+16x-32\right)\left(4x^2-36\right)\)
\(=-2\left(x^2-8x+16\right)\left[\left(2x\right)^2-6^2\right]\)
\(=-2\left(x-4\right)^2\left(2x-6\right)\left(2x+6\right)\)
\(=-2\left(x-4\right)^24\left(x-3\right)\left(x+3\right)\)
\(=8\left(x-4\right)^2\left(x-3\right)\left(x+3\right)\)
Cho hai đa thức A= 2 x 4 - 10 x 3 + 3 x 2 - 3 x + 2 ; B = 2 x 2 + 1 .Tìm đa thức dư R trong phép chia A cho B rồi viết A= B.Q + R
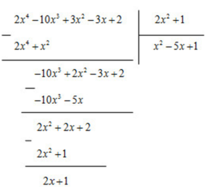
A = 2 x 2 + 1 x 2 - 5 x + 1 + 2 x + 1
Vậy đa thức dư R của phép chia A cho B là R = 2x + 1. Khi đó:
2 x 4 - 10 x 3 + 3 x 2 - 3 x + 2 = 2 x 2 + 1 x 2 - 5 x + 1 + 2 x + 1