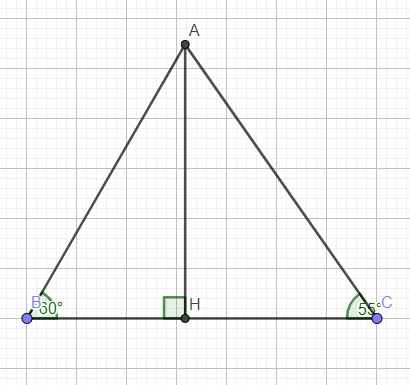
Cho tam giác ABC có \(\widehat{A}=60\) độ; \(\widehat{B}< \widehat{C}\). Hãy so sánh độ dài 3 cạnh của tam giác ABC.

Những câu hỏi liên quan
Cho tam giác ABC có \(\widehat{B}=2\widehat{C}\)
a) Chứng minh : \(\widehat{C}< 60\) độ
b) Tìm điều kiện của \(\widehat{C}\) để chọn tam giác ABC là tam giác nhọn
a)
C < 60 vì A + B + C = A + 3C ( VÌ B = 2C )
mà C = 60 =) A + 180 = 180
=) A = 0
Vậy C < 60 để A thõa mãn
Vậy C < 60
Đúng 0
Bình luận (0)
Muon
tam giác ABC là tam giác nhọn
=) C < 90 độ
=) C + B < 180 độ
=) 3C < 180 độ
=) C < 60 độ
Vậy C < 60 độ để tam giác ABC là tam giác nhọn
Đúng 0
Bình luận (0)
Cho tam giác ABC cân tại A có \(\widehat{BAC}\) = 70 độ. Điểm D nằm trong tam giác ABC sao cho DA = DB và \(\widehat{CAD}\) = 65 độ. Tính \(\widehat{BCD}\)
Cho hai tam giác ABC và A’B’C’ thỏa mãn: BC = B’C’ = 3 cm, \(\widehat B = \widehat {B'} = 60^\circ ,\widehat C = 50^\circ ,\widehat {A'} = 70^\circ \). Hai tam giác ABC và A’B’C’ có bằng nhau không? Vì sao?
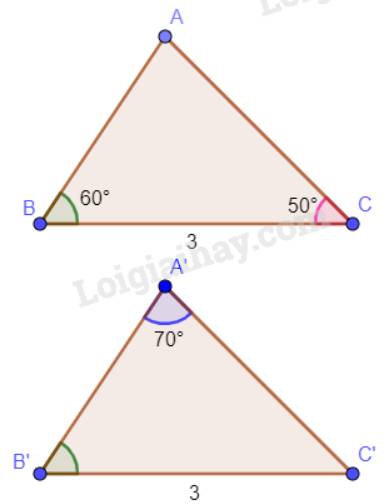
Tổng ba góc trong một tam giác bằng 180°. Vậy trong tam giác A’B’C’ có \(\widehat {C'} = 180^\circ - 70^\circ - 60^\circ = 50^\circ \).
Xét hai tam giác ABC và A’B’C’ có:
\(\widehat B = \widehat {B'} = 60^\circ ;\)
BC = B’C’ ( = 3 cm)
\(\widehat C = \widehat {C'} = 50^\circ \)
Vậy \(\Delta ABC = \Delta A'B'C'\)(g.c.g)
Đúng 0
Bình luận (0)
Cho tam giác ABC có AB = 12; \(\widehat B = {60^o}\); \(\widehat C = {45^o}\). Tính diện tích của tam giác ABC.
Áp dụng định lí sin trong tam giác ABC, ta có:
\(\frac{{AC}}{{\sin B}} = \frac{{AB}}{{\sin C}}\)
\( \Rightarrow AC = \sin B.\frac{{AB}}{{\sin C}} = \sin {60^o}.\frac{{12}}{{\sin {{45}^o}}} = 6\sqrt 6 \)
Lại có: \(\widehat A = {180^o} - ({60^o} + {45^o}) = {75^o}\)
\( \Rightarrow \)Diện tích tam giác ABC là:
\(S = \frac{1}{2}AB.AC.\sin A = \frac{1}{2}.12.6\sqrt 6 .\sin {75^o} \approx 85,2\)
Vậy diện tích tam giác ABC là 85,2.
Đúng 0
Bình luận (0)
Cho hai tam giác ABC và A’B’C’ (Hình 57) có: \(\widehat A = \widehat {A'} = 60^\circ \), AB = A’B’ = 3 cm, \(\widehat B = \widehat {B'} = 45^\circ \). Bằng cách đếm số ô vuông, hãy so sánh BC và B’C’. Từ đó có thể kết luận được hai tam giác ABC và A’B’C’ bằng nhau hay không?
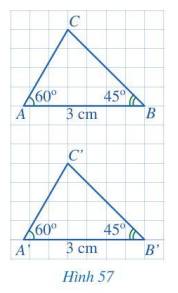
BC = B’C’ = 4 (đường chéo của 4 ô vuông).
Tam giác ABC và tam giác A’B’C’ có: BC = B’C’, AB = A’B’, \(\widehat B = \widehat {B'}\).
Vậy \(\Delta ABC = \Delta A'B'C'\)(c.g.c)
Đúng 0
Bình luận (0)
Bài 1: Cho tam giác ABC có \(\widehat{B}=60^o\), \(\widehat{C}=55^o\), AC = 4,5cm. Tính diện tích tam giác ABC?
Kẻ đường cao AH ứng với BC
Trong tam giác vuông ACH:
\(sinC=\dfrac{AH}{AC}\Rightarrow AH=AC.sinC\)
\(cosC=\dfrac{CH}{AC}\Rightarrow CH=AC.cosC\)
Trong tam giác vuông ABH:
\(tanB=\dfrac{AH}{BH}\Rightarrow BH=\dfrac{AH}{tanB}=\dfrac{AC.sinC}{tanB}\)
Do đó:
\(S_{ABC}=\dfrac{1}{2}AH.BC=\dfrac{1}{2}AH\left(BH+CH\right)=\dfrac{1}{2}.4,5.sin55^0.\left(\dfrac{4,5.sin55^0}{tan60^0}+4,5.cos55^0\right)\approx8,68\left(cm^2\right)\)
Đúng 2
Bình luận (0)
Cho tam giác ABC có \(\widehat{A}\)= 60 độ . Vẽ ra phía ngoài của tam giác 2 tam giác AMB và ANC.
a) CMR: 3đ M,A,N thẳng hàng
b)CMR: BN=CM
2 tam giác AMB và tam giác ANC có đk gì k, hình như đề bài hơi thếu ^_^
Đúng 0
Bình luận (0)
\(\Delta AMB\)và \(\Delta ANC\) đều đấy vũ tiền châu
Đúng 0
Bình luận (0)
Hình hơi xấu chút
ta có tam giác ABM và tam giác ACN là các tam giác đều
=>\(\widehat{BAM}=\widehat{CAN}=60^0\Rightarrow\widehat{BAM}+\widehat{CAN}+\widehat{BAC}=60^o+60^o+60^o=180^O\)
=> M,A,N thẳng hàng (ĐPCM)
b) Xét tam giác AMC và tam giác ANB có
\(\hept{\begin{cases}\widehat{MAC}=\widehat{NAB}=120^o\\AN=AC\\AM=AB\end{cases}}\Rightarrow\Delta MAC=\Delta NAB\left(c-g-c\right)\Rightarrow BN=CM\left(ĐPCM\right)\)
Đúng 1
Bình luận (2)
Cho tam giác ABC có \(\widehat{B}>\widehat{C}\) . Tia phân giác ngoài của \(\widehat{A}\) cắt BC tại E
a) Chứng minh : \(\widehat{AED}=\frac{\widehat{ABC}-\widehat{ACB}}{2}\)
b) Cho \(\widehat{BAC}=60\) độ, \(\widehat{AEB}=15\) độ
Tính \(\widehat{B},\widehat{C}\)
Cho tam giác ABC có\(_{\widehat{ }C}\)=60 ,\(\widehat{A}=2\widehat{B}\)
So sánh 3 cạnh tam giác
Cho tam giác ABC bằng tam giác DEF (H. 4.13). Biết rằng BC = 4 cm, \(\widehat {ABC} = 40^\circ ;\widehat {ACB} = 60^\circ \). Hãy tính độ dài đoạn thẳng EF và số đo góc EDF.
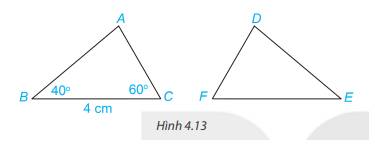
Vì \(\Delta ABC = \Delta DEF\) nên BC = EF ( 2 cạnh tương ứng); \(\widehat A = \widehat {EDF}\) ( 2 góc tương ứng)
Mà BC = 4 cm nên EF = 4 cm
Trong tam giác ABC có: \(\widehat A + \widehat B + \widehat C = 180^\circ \) ( định lí tổng ba góc trong một tam giác)
\(\begin{array}{l} \Rightarrow \widehat A + 40^\circ + 60^\circ = 180^\circ \\ \Rightarrow \widehat A = 180^\circ - 40^\circ - 60^\circ = 80^\circ \end{array}\)
Mà \(\widehat A = \widehat {EDF}\) nên \(\widehat {EDF} = 80^\circ \)
Đúng 0
Bình luận (0)