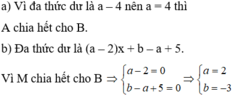tìm a,b ϵ Q để đa thức A(x) = x4+ a.x3 +b Khi đó ta có thể chia hết cho B(x) = x2 -1

Những câu hỏi liên quan
Cho đa thức A(x) = 1 + x2 + x4 + .... + x2n - 2; B= 1 + x + x2 + ... + xn-1. Tìm số nguyên dương n để đa thức A(x) chia hết cho đa thức B(x).
A(x)=(1-x^n)(1+x^n)/(1-x)(1+x)
B(x)=1-x^n/1-x
A(x) chia hết cho B(x) khi 1-x^n chia hết cho 1+x
x^n+1/x+1=A(x)+(1+(-1)^n)/(x+1)
=>1-x^n chia hết cho 1+x khi và chỉ khi n=2k+1
Đúng 1
Bình luận (1)
Tìm a và b để đa thức A chia hết cho đa thức B với:a) A
x
4
-
x
3
+
6
x
2
- x + a và B
x
2
- x + 5;b) A
x
4
-
9
x
3
+ 21
x
2
+...
Đọc tiếp
Tìm a và b để đa thức A chia hết cho đa thức B với:
a) A = x 4 - x 3 + 6 x 2 - x + a và B = x 2 - x + 5;
b) A = x 4 - 9 x 3 + 21 x 2 +ax + b và B = x 2 - x - 2.

Hay a − 1 = 0 b + 30 = 0 ⇒ a = 1 b = − 30 .
Đúng 0
Bình luận (0)
Cho đa thức: A=x4-7x3+10x2+(a-1)x+b-a và B=x2-6x+5. Tìm a và b để đa thức A chia hết cho đa thức B
Ta thấy \(B=\left(x-1\right)\left(x-5\right)\) nên để đa thức A chia hết cho đa thức B thì \(A=\left(x-1\right)\left(x-5\right).C\) với \(C\) là một đa thức bậc 2 hệ số nguyên theo \(x\).
Điều này tương đương với việc \(A\) có 2 nghiệm là \(x=1,x=5\). Do đó \(A\left(1\right)=0\) \(\Leftrightarrow1^4-7.1^3+10.1^2+\left(a-1\right)+b-a=0\) \(\Leftrightarrow b=-3\)
Ta viết lại \(A=x^4-7x^3+10x^2+\left(a-1\right)x-3-a\). Ta có \(A\left(5\right)=0\) \(\Leftrightarrow5^4-7.5^3+10.5^2+\left(a-1\right).5-3-a=0\) \(\Leftrightarrow4a-8=0\) \(\Leftrightarrow a=2\).
Vậy để đa thức A chia hết cho đa thức B thì \(a=2,b=-3\).
Đúng 3
Bình luận (0)
A:B=x2-x+11 dư (a+70)x+b-a-55
Để A chia hết cho B thì
(a+70)x+b-a-55=0
b-a-55=0 (a khác -70) tại x=0
Vậy b-a=55 thỏa đề bài
Đúng 0
Bình luận (0)
Tìm các số nguyên a và b để đa thức A(x)=x4-3x3+ax +b chia hết cho đa thức
B(x)=x2-3x+4
bạn trúc giang sai rồi -4 nhân -3x sao lại bằng -12x
Đúng 0
Bình luận (0)
Tìm a và b để đa thức f(x)
x
4
–
9
x
3
+
21
x
2
+ ax + b chia hết cho đa thức g(x)
x
2
– x – 2 A. a -1; b 30 B. a 1; b 30 C. a -1; b -30 D. a 1; b -30
Đọc tiếp
Tìm a và b để đa thức f(x) = x 4 – 9 x 3 + 21 x 2 + ax + b chia hết cho đa thức g(x) = x 2 – x – 2
A. a = -1; b = 30
B. a = 1; b = 30
C. a = -1; b =-30
D. a = 1; b = -30
Ta có

Phần dư của phép chia f(x) cho g(x) là R = (a – 1)x + b + 30
Để phép chia trên là phép chia hết thì R = 0 với mọi x
ó (a – 1)x + b + 30 = 0 với mọi x
ó a - 1 = 0 b + 30 = 0 ó a = 1 b = - 30
Vậy a = 1; b = -30
Đáp án cần chọn là: D
Đúng 0
Bình luận (0)
Biết đa thức
x
4
+ a
x
2
+ b chia hết cho
x
2
– x + 1. Khi đó, khẳng định nào sau đây là đúng. A. a b B. a b C. a b D. a 2b
Đọc tiếp
Biết đa thức x 4 + a x 2 + b chia hết cho x 2 – x + 1. Khi đó, khẳng định nào sau đây là đúng.
A. a < b
B. a > b
C. a = b
D. a = 2b
Ta có
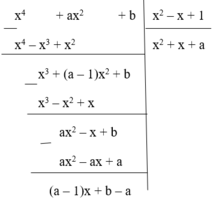
Phần dư của phép chia là R = (a – 1)x + b – A. Để phép chia trên là phép chia hết thì R = 0, Ɐx
ó (a – 1)x + b – a = 0, Ɐx
ó a - 1 = 0 b - a = 0 ó a = 1 b = 1 ó a = b
Đáp án cần chọn là: C
Đúng 0
Bình luận (0)
Tìm a và b để đa thức A chia hết cho đa thức B với:a) A
4
x
3
+
15
x
2
+ 24x + 3 + a và B
x
2
+ 4x + 7;b) A
x
4
+
3
x
3
-
x
2
+ (2a - 3)x +...
Đọc tiếp
Tìm a và b để đa thức A chia hết cho đa thức B với:
a) A = 4 x 3 + 15 x 2 + 24x + 3 + a và B = x 2 + 4x + 7;
b) A = x 4 + 3 x 3 - x 2 + (2a - 3)x + 3b + a và B = x 2 + 3x - 1.
Tìm a và b để đa thức A chia hết cho đa thức B với:a) A
x
3
-
9
x
2
+17x - 25 + a và B
x
2
- 2x + 3;b) A
x
4
-
7
x
3
+
10
x
2
+(a - 1)x + b...
Đọc tiếp
Tìm a và b để đa thức A chia hết cho đa thức B với:
a) A = x 3 - 9 x 2 +17x - 25 + a và B = x 2 - 2x + 3;
b) A = x 4 - 7 x 3 + 10 x 2 +(a - 1)x + b - a và B = x 2 -6x + 5.
a/ Tìm a sao cho đa thức : x4 – x3 + 6x2 – x + a chia hết cho đa thức: x2 – x + 5
b/ Tính giá trị nguyên của n để giá trị của biểu thức : 3n3 + 10n2 – 5 chia hết cho giá trị của biểu thức: 3n + 1
b: \(\Leftrightarrow3n^3+n^2+9n^2+3n-3n-1-4⋮3n+1\)
\(\Leftrightarrow3n+1\in\left\{1;-1;2;-2;4;-4\right\}\)
\(\Leftrightarrow n\in\left\{0;-1;1\right\}\)
Đúng 1
Bình luận (0)