.Cho tam giác ABC , đường phân giác trong của C cắt cạnh AB tại D. Chứng minh rằng CD2 < CA.CB

Những câu hỏi liên quan
Bài 6.Cho tam giác ABC , đường phân giác trong của C cắt cạnh AB tại D. Chứng minh rằng CD2 < CA.CB
Cho tam giác ABC, đường phân giác trong của C cắt cạnh AB tại D. Chứng minh rằng \(CD^2< CA.CB\)
Học đến tính chât tia phân giác chia thành tỷ lệ chưa
\(\Delta ABC\)có: đường phân giác trong của C cắc cạnh AB tại D. Lấy điểm E trên tia CD sao cho \(\widehat{CBD}=\widehat{CEA}\)
Xét \(\Delta CBD\)và \(\Delta CEA\)có:
\(\widehat{BCD}=\widehat{ACD}\)( đường phân giác trong của C cắc cạnh AB tại D )
\(\widehat{CBD}=\widehat{CEA}\)
\(\Rightarrow\Delta CBD\)đồng dạng với \(\Delta CEA\left(g.g\right)\)
\(\Rightarrow\frac{CD}{CA}=\frac{BC}{EC}\Leftrightarrow BC.AC=EC.CD\)
Mà \(EC=CD+DE\)
nên \(BC.AC=CD\left(CD+DE\right)\)
\(\Leftrightarrow BC.AC=CD^2+CD.DE\)
\(\Rightarrow CD^2< CA.CB\)
Cho tam giác ABC vuông ở A biết AB = 8cm AC = 6cm, tia phân giác của góc A cắt cạnh huyền tại điểm D từ D kẻ đường thẳng vuông góc với AC cắt AB tại H chứng minh rằng a, tính độ dài BC b, chứng minh tam giác ABC đồng dạng với tam giác HDC c, tính tỉ số BD và DC tính tỉ số diện tích của tam giác ADH và tam giác ADC
a: \(BC=\sqrt{8^2+6^2}=10\left(cm\right)\)
b: Sửa đề: vuônggóc BC, cắt AC tại H
Xet ΔCDH vuông tại D và ΔCAB vuông tại A có
góc C chung
=>ΔCDH đồng dạng với ΔCAB
c: BD/DC=AB/AC=4/3
Đúng 0
Bình luận (0)
cho tam giác abc vuông tại a có c=30 độ tia phân giác của góc b cắt ac tại d
a)chứng minh rằng tam giác bdc là tam giác cân
b)qua d kẻ đường thẳng vuông góc với bc tại e cắt ab tại f chứng minh bf=bc
c)cho ab=4cm.tính chiều dài các cạnh của tam giác abc
Cho tam giác ABC , đường phân giác trong của C cắt cạnh AB tại D . Chứng minh rằng
\(CD^2\) < CA.CB
Cho tam giác ABC có \(\widehat A = 120^\circ \). Tia phân giác của góc A cắt cạnh BC tại D. Đường thẳng qua D song song với AB cắt cạnh AC tại E. Chứng minh rằng tam giác ADE đều.
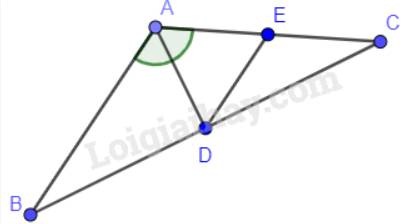
\(\widehat A = 120^\circ \)nên \(\widehat {DAE} = 60^\circ \)(AD là phân giác của góc A).
Ta có: DE // AB nên \(\widehat {CED} = \widehat {EAB} = 120^\circ \)(hai góc đồng vị). Ba điểm A, E, C thẳng hàng nên góc AEC bằng 180°
\(\Rightarrow \widehat {AED} = 180^\circ - \widehat {CED} = 180^\circ - 120^\circ = 60^\circ \)
Tam giác ADE có \(\widehat {EAD} = \widehat {ADE}\) (\(=60^0\)) nên là tam giác cân.
Mà \(\widehat {DEA} = 60^\circ \)
Do đó, tam giác ADE đều ( tam giác cân có 1 góc bằng \(60^0\)).
Đúng 0
Bình luận (0)
Cho tam giác ABC có ba góc nhọn và ABAC. Tam giác ABC nội tiếp đường tròn (O;R). Đường cao AH của tam giác ABC cắt đường tròn (O;R) tại điểm thứ hai là D. Kẻ DM vuông góc với AB tại M.a) Chứng minh tứ giác BDHM nội tiếp đường tròn.b) Chứng minh DA là tia phân giác của MDCc) Gọi N là hình chiếu vuông góc của D lên đường thẳng AC, chứng minh ba điểm M, H, N thẳng hàng.d) Chứng minh AB2 + AC2 + CD2 + BD2 8R2
Đọc tiếp
Cho tam giác ABC có ba góc nhọn và AB>AC. Tam giác ABC nội tiếp đường tròn (O;R). Đường cao AH của tam giác ABC cắt đường tròn (O;R) tại điểm thứ hai là D. Kẻ DM vuông góc với AB tại M.
a) Chứng minh tứ giác BDHM nội tiếp đường tròn.
b) Chứng minh DA là tia phân giác của MDC
c) Gọi N là hình chiếu vuông góc của D lên đường thẳng AC, chứng minh ba điểm M, H, N thẳng hàng.
d) Chứng minh AB2 + AC2 + CD2 + BD2 = 8R2
Cho tam giác ABC vuông tại A có AB AC. Lấy M là một điểm tùy ý trên cạnh BC. Qua M kẻ đường thẳng vuông góc với BC và cắt đoạn thẳng AB tại điểm I, cắt đường thẳng AC tại điểm D.a) Chứng minh: ∆ABC đồng dạng ∆MDCb) Chứng minh rằng: BI.BA BM.BCc) Chứng minh: góc BAM ICB. Từ đó chứng minh AB là phân giác của góc MAK với K là giao điểm của CI và BDd) Cho AB 8cm, AC 6cm. Khi AM là đường phân giác trong tam giác ABC hãy tính diện tích tứ giác AMBD
Đọc tiếp
Cho tam giác ABC vuông tại A có AB > AC. Lấy M là một điểm tùy ý trên cạnh BC. Qua M kẻ đường thẳng vuông góc với BC và cắt đoạn thẳng AB tại điểm I, cắt đường thẳng AC tại điểm D.
a) Chứng minh: ∆ABC đồng dạng ∆MDC
b) Chứng minh rằng: BI.BA = BM.BC
c) Chứng minh: góc BAM = ICB. Từ đó chứng minh AB là phân giác của góc MAK với K là giao điểm của CI và BD
d) Cho AB = 8cm, AC = 6cm. Khi AM là đường phân giác trong tam giác ABC hãy tính diện tích tứ giác AMBD
Cho Tam Giác ABC, có BAC =120 đọ. đường phân giác trong của góc A cắt BC tại D.Từ D kẻ DE vuông góc với AB, DF vuông góc với AC.a)Chứng MInh tam giác ADE = ADF. b)Chứng minh rằng tam giác DEF là tam giác đều C) qua điểm C vẽ đường thẳng song song với AD, nó cắt đường thẳng AB tại M. Chứng minh rằng tam giác ACM là tam giác đèu
















