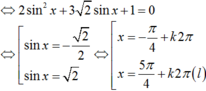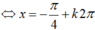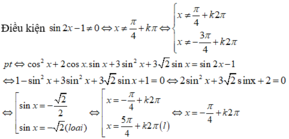a/ \(sin3x=sin\left(2x+x\right)=sin2xcosx+cos2x.sinx\)

\(=2sinxcos^2x+\left(1-2sin^2x\right)sinx=2sinx\left(1-sin^2x\right)+sinx-2sin^3x\)

\(=3sinx-4sin^3x\)

b/

\(tan2x+\frac{1}{cos2x}=\frac{sin2x}{cos2x}+\frac{1}{cos2x}=\frac{sin2x+1}{cos2x}=\frac{2sinxcosx+sin^2x+cos^2x}{cos^2x-sin^2x}\)

\(=\frac{\left(sinx+cosx\right)^2}{\left(sinx+cosx\right)\left(cosx-sinx\right)}=\frac{sinx+cosx}{cosx-sinx}=\frac{\left(sinx+cosx\right)\left(cosx-sinx\right)}{\left(cos-sinx\right)^2}\)

\(=\frac{cos^2x-sin^2x}{cos^2x+sin^2x-2sinxcosx}=\frac{1-2sin^2x}{1-sin2x}\)

c/

\(\frac{cosx+sinx}{cosx-sinx}-\frac{cosx-sinx}{cosx+sinx}=\frac{\left(cosx+sinx\right)^2-\left(cosx-sinx\right)^2}{cos^2x-sin^2x}\)

\(=\frac{2sinxcosx+2sinxcosx}{cos2x}=\frac{4sinxcosx}{cos2x}=\frac{2sin2x}{cos2x}=2tan2x\)

d/

\(\frac{sin2x}{1+cos2x}=\frac{2sinxcosx}{1+2cos^2x-1}=\frac{2sinxcosx}{2cos^2x}=\frac{sinx}{cosx}=tanx\)

e/

1: tan x=3 nên sin x/cosx=3

=>sin x=3*cosx

\(B=\dfrac{2\cdot sinx-3cosx}{sinx+cosx}=\dfrac{2\cdot3\cdot cosx-3cosx}{3cosx+cosx}\)

\(=\dfrac{2\cdot3-3}{3+1}=\dfrac{3}{4}\)

2: tan x=-1 nên sin x/cosx=-1

=>sinx=-cosx

\(I=\dfrac{4\cdot\left(-cosx\right)^3+\left(cosx\right)^3}{-cosx+3\cdot cosx}=\dfrac{-3\cdot cos^3x}{2cosx}=-\dfrac{3}{2}\cdot cos^2x\)

\(1+tan^2x=\dfrac{1}{cos^2x}\)

=>\(\dfrac{1}{cos^2x}=1+1=2\)

=>\(cos^2x=\dfrac{1}{2}\)

=>I=-3/2*1/2=-3/4

1.

\(2sin\left(x+\dfrac{\pi}{6}\right)+sinx+2cosx=3\)

\(\Leftrightarrow\sqrt{3}sinx+cosx+sinx+2cosx=3\)

\(\Leftrightarrow\left(\sqrt{3}+1\right)sinx+3cosx=3\)

\(\Leftrightarrow\sqrt{13+2\sqrt{3}}\left[\dfrac{\sqrt{3}+1}{\sqrt{13+2\sqrt{3}}}sinx+\dfrac{3}{\sqrt{13+2\sqrt{3}}}cosx\right]=3\)

Đặt \(\alpha=arcsin\dfrac{3}{\sqrt{13+2\sqrt{3}}}\)

\(pt\Leftrightarrow\sqrt{13+2\sqrt{3}}sin\left(x+\alpha\right)=3\)

\(\Leftrightarrow sin\left(x+\alpha\right)=\dfrac{3}{\sqrt{13+2\sqrt{3}}}\)

\(\Leftrightarrow\left[{}\begin{matrix}x+\alpha=arcsin\dfrac{3}{\sqrt{13+2\sqrt{3}}}+k2\pi\\x+\alpha=\pi-arcsin\dfrac{3}{\sqrt{13+2\sqrt{3}}}+k2\pi\end{matrix}\right.\)

\(\Leftrightarrow\left[{}\begin{matrix}x=k2\pi\\x=\pi-2arcsin\dfrac{3}{\sqrt{13+2\sqrt{3}}}+k2\pi\end{matrix}\right.\)

Vậy phương trình đã cho có nghiệm:

\(x=k2\pi;x=\pi-2arcsin\dfrac{3}{\sqrt{13+2\sqrt{3}}}+k2\pi\)

2.

\(\left(sin2x+cos2x\right)cosx+2cos2x-sinx=0\)

\(\Leftrightarrow2sinx.cos^2x+cos2x.cosx+2cos2x-sinx=0\)

\(\Leftrightarrow\left(2cos^2x-1\right)sinx+cos2x.cosx+2cos2x=0\)

\(\Leftrightarrow cos2x.sinx+cos2x.cosx+2cos2x=0\)

\(\Leftrightarrow cos2x.\left(sinx+cosx+2\right)=0\)

\(\Leftrightarrow cos2x=0\)

\(\Leftrightarrow2x=\dfrac{\pi}{2}+k\pi\)

\(\Leftrightarrow x=\dfrac{\pi}{4}+\dfrac{k\pi}{2}\)

Vậy phương trình đã cho có nghiệm \(x=\dfrac{\pi}{4}+\dfrac{k\pi}{2}\)

=sin2x-1

`1)sin^2 x+3sin x-cos^2 x=-2`

`<=>sin^2 x+3sin x-1+sin^2 x+2=0`

`<=>2sin^2 x+3sin x+1=0`

`<=>[(sin x=-1),(sin x=-1/2):}`

`<=>[(x=-\pi/2 +k2\pi),(x=-\pi/6 +k2\pi),(x=[7\pi]/6+k2\pi):}`   `(k in ZZ)`

`2)sin^2 x+sin x-cos^2 x=0`

`<=>sin^2 x+sin x-1+sin^2 x=0`

`<=>2sin^2 x+sin x-1=0`

`<=>[(sin x=-1),(sin x=1/2):}`

`<=>[(x=-\pi/2 +k2\pi),(x=\pi/6 +k2\pi),(x=[5\pi]/6 +k2\pi):}`    `(k in ZZ)`

Đáp án D

\(y=\dfrac{sinx+1}{sinx}\)

ĐKXĐ: \(sinx\ne0\Rightarrow x\ne k\pi\)

\(y=\dfrac{sin2x+cosx}{tanx-sinx}\)

ĐKXĐ: \(\left\{{}\begin{matrix}cosx\ne0\\tanx-sinx\ne0\end{matrix}\right.\)

\(\Rightarrow\left\{{}\begin{matrix}cosx\ne0\\sinx\left(\dfrac{1}{cosx}-1\right)\ne0\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}cosx\ne0\\sinx\ne0\\cosx\ne1\end{matrix}\right.\)

\(\Rightarrow sin2x\ne0\)

\(\Rightarrow x\ne\dfrac{k\pi}{2}\)