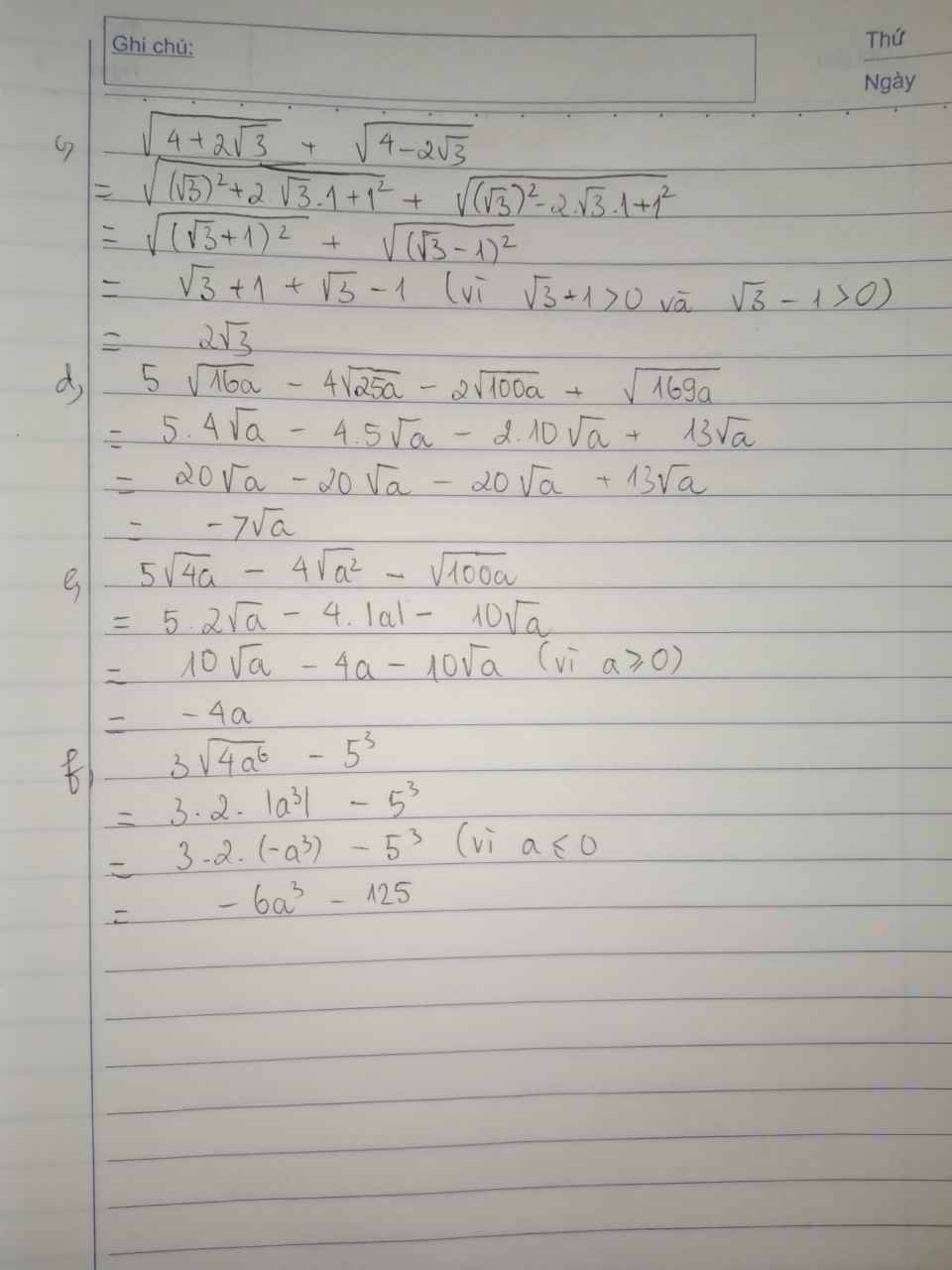a - \(4\sqrt{a}-5\)
Những câu hỏi liên quan
a) \(A = \sqrt[3]{{5\sqrt {\frac{1}{5}} }};\,\,a = 5\)
b) \(B = \frac{{4\sqrt[5]{2}}}{{\sqrt[3]{4}}};\,\,a = \sqrt 2 \)
a) \(A = \sqrt[3]{{5\sqrt {\frac{1}{5}} }} = \sqrt[3]{{a\sqrt {\frac{1}{a}} }} = \sqrt[3]{{a.{a^{\frac{1}{2}}}}} = \sqrt[3]{{{a^{\frac{3}{2}}}}} = {\left( {{a^{\frac{3}{2}}}} \right)^{\frac{1}{3}}} = {a^{\frac{3}{2}.\frac{1}{3}}} = {a^{\frac{1}{2}}} = \sqrt a \)
b) \(B = \frac{{4\sqrt[5]{2}}}{{\sqrt[3]{4}}} = \frac{{{2^2}{{.2}^{\frac{1}{5}}}}}{{{4^{\frac{1}{3}}}}} = \frac{{{2^{\frac{{11}}{5}}}}}{{{2^{\frac{2}{3}}}}} = {2^{\frac{{23}}{{15}}}}\)
\(a = \sqrt 2 = {2^{\frac{1}{2}}}\)
=> \(B = {a^{\frac{{23}}{{30}}}}\)
Đúng 0
Bình luận (0)
20 tháng 5 2023 lúc 14:10
Rút gọn các biểu thức sau:
A = \(5\sqrt{a}+6\sqrt{\dfrac{a}{4}}-a\sqrt{\dfrac{4}{a}}+5\sqrt{a}\); \(a>0\)
B = \(3\sqrt{5a}-\sqrt{20a}+4\sqrt{45a}+\sqrt{5a};a\ge0\)
Rút gọn: A = \(\frac{a+\sqrt{2+\sqrt{5}}.\sqrt{\sqrt{9-4\sqrt{5}}}}{\sqrt[3]{2-\sqrt{5}}.\sqrt[3]{\sqrt{9-4\sqrt{5}}}-\sqrt[3]{a^2}+\sqrt[3]{a}}\)
Chứng minh:
\(\dfrac{a+\sqrt{2+\sqrt{5}}.\sqrt{\sqrt{9-4\sqrt{5}}}}{\sqrt[3]{2-\sqrt{5}}.\sqrt[3]{\sqrt{9+4\sqrt{5}}}-\sqrt[3]{a^2}+\sqrt[3]{a}}=-\sqrt[3]{a}-1\)
rút gọn các biểu thức sau
c,\(\sqrt{4+2\sqrt{3}}+\sqrt{4-2\sqrt{3}}\) d,\(5\sqrt{16a}-4\sqrt{25a}-2\sqrt{100a}+\sqrt{169a}\) với a ≥ 0
e,\(5\sqrt{4a}-4\sqrt{a^2}-\sqrt{100a}\) với a ≥ 0 f,\(3\sqrt{4a^6}-5^3\) với a ≤ 0
A = \(2.\sqrt{\dfrac{2\sqrt{5}+4}{2\sqrt{5}-4}}+5\sqrt{\dfrac{1}{5}}-\sqrt{45}\)
rút gọn A
\(A=2\cdot\sqrt{9+4\sqrt{5}}+\sqrt{5}-3\sqrt{5}\)
=2(căn 5+2)-2căn 5
=4
Đúng 1
Bình luận (1)
Rút gọn các biểu thức sau đây:
a) $M=5 \sqrt{\dfrac{1}{5}}+\dfrac{5}{2} \sqrt{\dfrac{4}{5}}-3 \sqrt{5}$;
b) $N=3 \sqrt{\dfrac{1}{2}}+\sqrt{4,5}-\sqrt{12,5}$;
c) $P=\sqrt{\dfrac{1}{3}}+\sqrt{1 \dfrac{1}{5}}+4 \sqrt{3}$ :
d) $Q=2 \sqrt{a}-a \sqrt{\dfrac{4}{a}}+a^{2} \sqrt{\dfrac{9}{a^{3}}}$.
a) M=-căn 5
b) N=căn 2/2
c) P=5 căn 3
d) Q=3 căn a
Đúng 0
Bình luận (0)
M=-√5
N=√2/2
P= 3√30 +65√3 / 15
Q=3√a
Đúng 0
Bình luận (0)
M=-√5
N=√2/2
P= 3√30 +65√3 / 15
Q=3√a
Đúng 0
Bình luận (0)
SGK Cánh Diều
13 tháng 8 2023 lúc 21:42
Dựa vào tính chất lũy thừa để tính
a) \(A = \sqrt[3]{{5\sqrt {\frac{1}{5}} }};\,\,a = 5\)
b) \(B = \frac{{4\sqrt[5]{2}}}{{\sqrt[3]{4}}};\,\,a = \sqrt 2 \)
SGK Kết nối tri thức và cuộc sống
18 tháng 8 2023 lúc 18:00
Viết các biểu thức sau dưới dạng một luỹ thừa \(\left( {a > 0} \right)\):
a) \(3.\sqrt 3 .\sqrt[4]{3}.\sqrt[8]{3}\);
b) \(\sqrt {a\sqrt {a\sqrt a } } \);
c) \(\frac{{\sqrt a .\sqrt[3]{a}.\sqrt[4]{a}}}{{{{\left( {\sqrt[5]{a}} \right)}^3}.{a^{\frac{2}{5}}}}}\).
a: \(=3\cdot3^{\dfrac{1}{2}}\cdot3^{\dfrac{1}{.4}}\cdot3^{\dfrac{1}{8}}=3^{1+\dfrac{1}{2}+\dfrac{1}{4}+\dfrac{1}{8}}=3^{\dfrac{15}{16}}\)
b: \(=\sqrt{a\cdot\sqrt{a\cdot a^{\dfrac{1}{2}}}}\)
\(=\sqrt{a\cdot\sqrt{a^{\dfrac{3}{2}}}}=\sqrt{a\cdot a^{\dfrac{3}{4}}}=\sqrt{a^{\dfrac{7}{4}}}=a^{\dfrac{7}{4}\cdot\dfrac{1.}{2}}=a^{\dfrac{7}{8}}\)
c: \(=\dfrac{a^{\dfrac{1}{2}}\cdot a^{\dfrac{1}{3}}\cdot a^{\dfrac{1}{4}}}{\left(a^{\dfrac{1}{5}}\right)^3\cdot a^{\dfrac{2}{5}}}=\dfrac{a^{\dfrac{13}{12}}}{a}=a^{\dfrac{1}{12}}\)
Đúng 1
Bình luận (0)
Chứng minh đẳng thức sau:
\(\frac{a+\sqrt{2+\sqrt{5}}.\sqrt{\sqrt{9-4\sqrt{5}}}}{\sqrt[3]{2-\sqrt{5}}.\sqrt[3]{\sqrt{9+4\sqrt{5}}-\sqrt[3]{a^2}}+\sqrt[3]{a}}=-\sqrt[3]{a-1}\)
Chứng minh bất đẳng thức sau:
\(\left(\sqrt[3]{\sqrt{9+4\sqrt{5}}+\sqrt[3]{2+\sqrt{5}}}\right).\sqrt[3]{\sqrt{5-2}}-2,1< 0\)