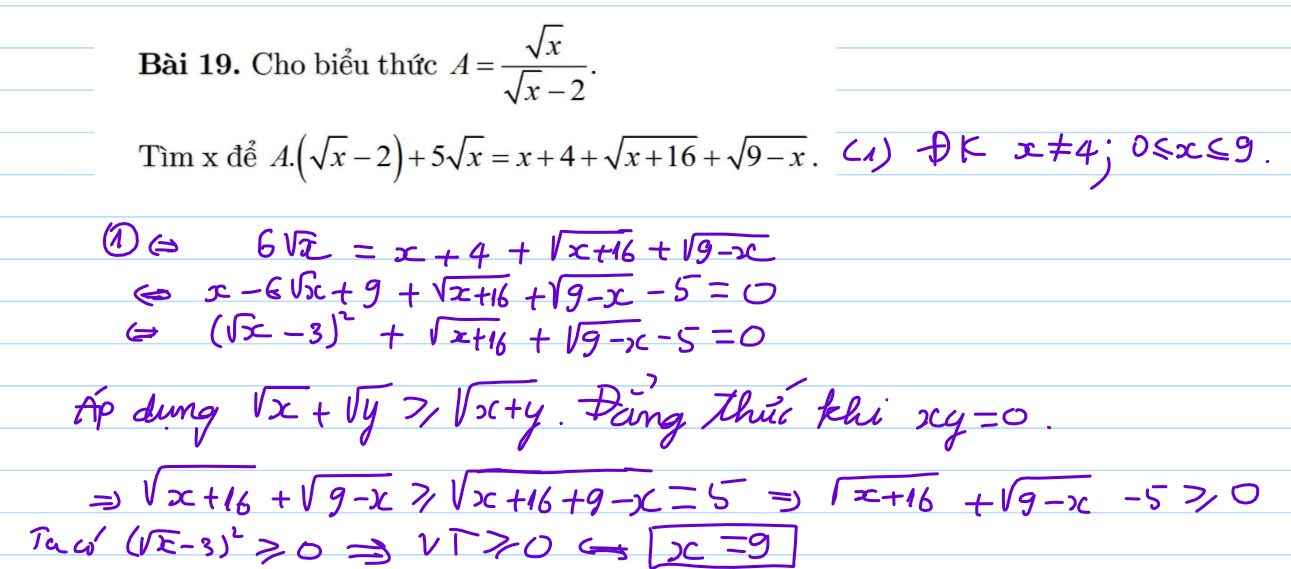Lời giải:

a. ĐKXĐ: $x\geq -9$

PT $\Leftrightarrow x+9=7^2=49$

$\Leftrightarrow x=40$ (tm)

b. ĐKXĐ: $x\geq \frac{-3}{2}$

PT $\Leftrightarrow 4\sqrt{2x+3}-\sqrt{4(2x+3)}+\frac{1}{3}\sqrt{9(2x+3)}=15$

$\Leftrightarrow 4\sqrt{2x+3}-2\sqrt{2x+3}+\sqrt{2x+3}=15$

$\Leftrgihtarrow 3\sqrt{2x+3}=15$

$\Leftrightarrow \sqrt{2x+3}=5$

$\Leftrightarrow 2x+3=25$

$\Leftrightarrow x=11$ (tm)

c.

PT \(\Leftrightarrow \left\{\begin{matrix} 2x+1\geq 0\\ x^2-6x+9=(2x+1)^2\end{matrix}\right.\Leftrightarrow \left\{\begin{matrix} x\geq \frac{-1}{2}\\ 3x^2+10x-8=0\end{matrix}\right.\)

\(\Leftrightarrow \left\{\begin{matrix} x\geq \frac{-1}{2}\\ (3x-2)(x+4)=0\end{matrix}\right.\)

\(\Leftrightarrow x=\frac{2}{3}\)

d. ĐKXĐ: $x\geq 1$

PT \(\Leftrightarrow \sqrt{(x-1)+4\sqrt{x-1}+4}-\sqrt{(x-1)+6\sqrt{x-1}+9}=9\)

\(\Leftrightarrow \sqrt{(\sqrt{x-1}+2)^2}-\sqrt{(\sqrt{x-1}+3)^2}=9\)

\(\Leftrightarrow \sqrt{x-1}+2-(\sqrt{x-1}+3)=9\)

\(\Leftrightarrow -1=9\) (vô lý)

Vậy pt vô nghiệm.

a) \(\sqrt{x+9}=7\left(x\ge-9\right)\Rightarrow x+9=49\Rightarrow x=40\)

b) \(4\sqrt{2x+3}-\sqrt{8x+12}+\dfrac{1}{3}\sqrt{18x+27}=15\left(x\ge-\dfrac{3}{2}\right)\)

\(\Rightarrow4\sqrt{2x+3}-\sqrt{4\left(2x+3\right)}+\dfrac{1}{3}\sqrt{9\left(2x+3\right)}=15\)

\(\Rightarrow4\sqrt{2x+3}-2\sqrt{2x+3}+\sqrt{2x+3}=15\)

\(\Rightarrow3\sqrt{2x+3}=15\Rightarrow\sqrt{2x+3}=5\Rightarrow2x+3=25\Rightarrow x=11\)

c) \(\sqrt{x^2-6x+9}=2x+1\)

Vì \(VT\ge0\Rightarrow VP\ge0\Rightarrow x\ge-\dfrac{1}{2}\)

\(\Rightarrow\sqrt{\left(x-3\right)^2}=2x+1\Rightarrow\left|x-3\right|=2x+1\Rightarrow\left[{}\begin{matrix}x-3=2x+1\\x-3=-2x-1\end{matrix}\right.\)

\(\Rightarrow\left[{}\begin{matrix}x=-4\left(l\right)\\x=\dfrac{2}{3}\end{matrix}\right.\)

d) \(\sqrt{x+3+4\sqrt{x-1}}-\sqrt{x+8+6\sqrt{x-1}}=9\left(x\ge1\right)\)

\(\Rightarrow\sqrt{x-1+4\sqrt{x-1}+4}-\sqrt{x-1+6\sqrt{x-1}+9}=9\)

\(\Rightarrow\sqrt{\left(\sqrt{x-1}+2\right)^2}-\sqrt{\left(\sqrt{x-1}+3\right)^2}=9\)

\(\Rightarrow\left|\sqrt{x-1}+2\right|-\left|\sqrt{x-1}+3\right|=9\)

\(\Rightarrow\sqrt{x-1}+2-\sqrt{x-1}-3=9\Rightarrow-1=9\) (vô lý)

Ta có:

\(B=\dfrac{x}{x-4}+\dfrac{1}{\sqrt{x}-2}+\dfrac{1}{\sqrt{x}+2}\) (ĐK: \(x\ne4;x\ge0\)) 

\(B=\dfrac{x}{\left(\sqrt{x}\right)^2-2^2}+\dfrac{1}{\sqrt{x}-2}+\dfrac{1}{\sqrt{x}+2}\)

\(B=\dfrac{x}{\left(\sqrt{x}+2\right)\left(\sqrt{x}-2\right)}+\dfrac{\sqrt{x}+2}{\left(\sqrt{x}+2\right)\left(\sqrt{x}-2\right)}+\dfrac{\sqrt{x}-2}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+2\right)}\)

\(B=\dfrac{x+\sqrt{x}+2+\sqrt{x}-2}{\left(\sqrt{x}+2\right)\left(\sqrt{x}-2\right)}\)

\(B=\dfrac{x+2\sqrt{x}}{\left(\sqrt{x}+2\right)\left(\sqrt{x}-2\right)}\)

\(B=\dfrac{\sqrt{x}\left(\sqrt{x}+2\right)}{\left(\sqrt{x}+2\right)\left(\sqrt{x}-2\right)}\)

\(B=\dfrac{\sqrt{x}}{\sqrt{x}-2}\)

\(\Rightarrow P=\dfrac{A}{B}=\dfrac{\dfrac{\sqrt{x}+2}{\sqrt{x}}}{\dfrac{\sqrt{x}}{\sqrt{x}-2}}=\dfrac{\left(\sqrt{x}+2\right)\left(\sqrt{x}-2\right)}{\sqrt{x}\cdot\sqrt{x}}=\dfrac{x-4}{x}\) (ĐK: \(x\ne0\)) 

Theo đề ta có:

\(P\cdot x\le10\sqrt{x}-29-\sqrt{x}+25\) (ĐK: \(x\ge0\)) 

\(\Leftrightarrow\dfrac{x-4}{x}\cdot x\le9\sqrt{x}-4\)

\(\Leftrightarrow x-4\le9\sqrt{x}-4\)

\(\Leftrightarrow x-9\sqrt{x}\le0\)

\(\Leftrightarrow\sqrt{x}\left(\sqrt{x}-9\right)\le0\)

Mà: \(\sqrt{x}\ge0\)

\(\Leftrightarrow\sqrt{x}-9\le0\)

\(\Leftrightarrow\sqrt{x}\le9\)

\(\Leftrightarrow x\le81\)

Kết hợp với đk:

\(0\le x\le81\)

Đáp án chi tiết

Cách số 2 

Cách số 2

Phần a,b,c bạn có thể tham khảo bài bên dưới. 

Phần d.

ĐKXĐ: $x\geq 0; x\neq 4$

$A>5\Leftrightarrow \frac{x+9}{2\sqrt{x}}>5$ ($x> 0$)

$\Leftrightarrow x+9> 10\sqrt{x}$

$\Leftrightarrow x-10\sqrt{x}+9>0$

$\Leftrightarrow (\sqrt{x}-1)(\sqrt{x}-9)>0$

\(\Leftrightarrow \left[\begin{matrix} \left\{\begin{matrix} \sqrt{x}-1>0\\ \sqrt{x}-9>0\end{matrix}\right.\\ \left\{\begin{matrix} \sqrt{x}-1<0\\ \sqrt{x}-9<0\end{matrix}\right.\end{matrix}\right.\Leftrightarrow \left[\begin{matrix} \left\{\begin{matrix} x>1\\ x>81\end{matrix}\right.\\ \left\{\begin{matrix} 0\leq x< 1\\ 0\leq x< 81\end{matrix}\right.\end{matrix}\right.\)

\(\Leftrightarrow \left[\begin{matrix} x>81\\ 0\leq x< 1\end{matrix}\right.\)

Kết hợp với đkxđ suy ra $x>81$ hoặc $0< x< 1$

a

Với: x \(\ge0,x\) \(\ne4\) có:

\(A=\left(\dfrac{x-\sqrt{x}+7}{x-4}+\dfrac{\sqrt{x}+2}{x-4}\right):\left(\dfrac{\left(\sqrt{x}+2\right)^2}{x-4}-\dfrac{\left(\sqrt{x}-2\right)^2}{x-4}-\dfrac{6\sqrt{x}}{x-4}\right)\)

\(=\left(\dfrac{x-\sqrt{x}+7+\sqrt{x}+2}{x-4}\right):\left(\dfrac{x+4\sqrt{x}+4}{x-4}-\dfrac{x-4\sqrt{x}+4}{x-4}-\dfrac{6\sqrt{x}}{x-4}\right)\)

\(=\left(\dfrac{x+9}{x-4}\right):\left(\dfrac{x+4\sqrt{x}+4-x+4\sqrt{x}-4-6\sqrt{x}}{x-4}\right)\)

\(=\left(\dfrac{x+9}{x-4}\right):\left(\dfrac{2\sqrt{x}}{x-4}\right)\)

\(=\dfrac{\left(x+9\right)\left(x-4\right)}{2\sqrt{x}\left(x-4\right)}=\dfrac{x+9}{2\sqrt{x}}\)

b

Giải \(x^2-5x+4=0\)

Nhẩm nghiệm: a + b + c = 0 (1 - 5 + 4 = 0)

\(\Rightarrow x_1=1;x_2=\dfrac{c}{a}=\dfrac{4}{1}=4\)

Thay x = 1 vào A:

\(A=\dfrac{1+9}{2\sqrt{1}}=\dfrac{10}{2}=5\)

Thay x = 4 vào A:

\(A=\dfrac{4+9}{2.\sqrt{4}}=\dfrac{13}{2.2}=\dfrac{13}{4}\)

c

ĐK: x > 0

\(A=0\Leftrightarrow\dfrac{x+9}{2\sqrt{x}}=0\)

=> \(x+9=0\Rightarrow x=-9\) (không thỏa mãn)

Vậy không xác định được giá trị x

d

ĐK: x > 0 

\(A>5\Leftrightarrow\dfrac{x+9}{2\sqrt{x}}>5\)

\(\Leftrightarrow x+9>5.2\sqrt{x}\Leftrightarrow x+9>10\sqrt{x}\)

\(\Leftrightarrow\left(x+9\right)^2>\left(10\sqrt{x}\right)^2=100x\)

<=> \(x^2+18x+81-100x>0\)

<=> \(x^2-82x+81>0\)

<=> \(x^2-81x-x+81>0\)

<=> \(x\left(x-81\right)-\left(x-81\right)>0\)

<=> \(\left(x-1\right)\left(x-81\right)>0\)

\(\Leftrightarrow\left\{{}\begin{matrix}\left[{}\begin{matrix}x-1>0\\x-81>0\end{matrix}\right.\\\left[{}\begin{matrix}x-1< 0\\x-81< 0\end{matrix}\right.\end{matrix}\right.\)

\(\Leftrightarrow\left\{{}\begin{matrix}\left[{}\begin{matrix}x>1\\x>81\end{matrix}\right.\\\left[{}\begin{matrix}x< 1\\x< 81\end{matrix}\right.\end{matrix}\right.\)

\(\Leftrightarrow\left\{{}\begin{matrix}x>81\\x< 81\end{matrix}\right.\)

Vậy để A > 5 thì x > 81 và 0 < x < 81

C.hóa \(x+y=1\) và dùng C-S:

\(VT^2\le\frac{2x}{\left(y+1\right)^2}+\frac{2y}{\left(x+1\right)^2}\le\frac{8}{9}=VP^2\)

\(BDT\Leftrightarrow\frac{x}{\left(2-x\right)^2}+\frac{y}{\left(2-y\right)^2}\le\frac{4}{9}\left(1\right)\)

Ta có BĐT phụ \(\frac{x}{\left(2-x\right)^2}\le\frac{20}{27}x-\frac{4}{27}\)

\(\Leftrightarrow-\frac{\left(2x-1\right)^2\left(5x-16\right)}{27\left(x-2\right)^2}\le0\) *Đúng*

Tương tự cho 2 BĐT còn lại rồi cộng theo vế:

\(VT_{\left(1\right)}\le\frac{20}{27}\left(x+y\right)-\frac{4}{27}\cdot2=\frac{4}{9}=VP_{\left(1\right)}\)

"=" khi \(x=y=\frac{1}{2}\)

a: \(B=\dfrac{1}{\sqrt{x}+1}\)

\(B-1=\dfrac{\sqrt{x}+1-1}{\sqrt{x}+1}=\dfrac{\sqrt{x}}{\sqrt{x}+1}>=0\)

=>B>=1

b: \(P=\dfrac{\sqrt{x}+1+x}{\sqrt{x}\left(\sqrt{x}+1\right)}\cdot\dfrac{\sqrt{x}\left(\sqrt{x}+1\right)}{\sqrt{x}}=\dfrac{x+\sqrt{x}+1}{\sqrt{x}}\)

\(P\cdot\sqrt{x}+2x-\sqrt{x}=3x-2\sqrt{x-4}+3\)

=>\(x+\sqrt{x}+1+2x-\sqrt{x}=3x+3-2\sqrt{x-4}\)

=>\(-2\sqrt{x-4}+3=1\)

=>x-4=1

=>x=5

a. ĐKXĐ: $x\geq 1$

PT $\Leftrightarrow \frac{1}{2}\sqrt{x-1}-\frac{3}{2}.\sqrt{9}.\sqrt{x-1}+24.\sqrt{\frac{1}{64}}.\sqrt{x-1}=-17$

$\Leftrightarrow \frac{1}{2}\sqrt{x-1}-\frac{9}{2}\sqrt{x-1}+3\sqrt{x-1}=-17$

$\Leftrightarrow -\sqrt{x-1}=-17$

$\Leftrightarrow \sqrt{x-1}=17$

$\Leftrightarrow x-1=289$

$\Leftrightarrow x=290$

b. ĐKXĐ: $x\geq \frac{1}{2}$

PT $\Leftrightarrow \sqrt{9}.\sqrt{2x-1}-0,5\sqrt{2x-1}+\frac{1}{2}.\sqrt{25}.\sqrt{2x-1}+\sqrt{49}.\sqrt{2x-1}=24$

$\Leftrightarrow 3\sqrt{2x-1}-0,5\sqrt{2x-1}+2,5\sqrt{2x-1}+7\sqrt{2x-1}=24$
$\Leftrightarrow 12\sqrt{2x-1}=24$

$\Leftrihgtarrow \sqrt{2x-1}=2$

$\Leftrightarrow x=2,5$ (tm)

c. ĐKXĐ: $x\geq 2$

PT $\Leftrightarrow \sqrt{36}.\sqrt{x-2}-15\sqrt{\frac{1}{25}}\sqrt{x-2}=4(5+\sqrt{x-2})$

$\Leftrightarrow 6\sqrt{x-2}-3\sqrt{x-2}=20+4\sqrt{x-2}$

$\Leftrightarrow \sqrt{x-2}=-20< 0$ (vô lý)

Vậy pt vô nghiệm

d. ĐKXĐ: $x>\frac{-2}{3}$

PT $\Leftrightarrow \sqrt{\frac{1}{3x+2}}-\frac{1}{2}\sqrt{9}.\sqrt{\frac{1}{3x+2}}+\sqrt{16}.\sqrt{\frac{1}{3x+2}}-5\sqrt{\frac{1}{4}}\sqrt{\frac{1}{3x+2}}=1$

$\Leftrightarrow \sqrt{\frac{1}{3x+2}}-\frac{3}{2}\sqrt{\frac{1}{3x+2}}+4\sqrt{\frac{1}{3x+2}}-\frac{5}{2}\sqrt{\frac{1}{3x+2}}=1$

$\Leftrightarrow \sqrt{\frac{1}{3x+2}}=1$

$\Leftrightarrow \frac{1}{3x+2}=1$

$\Leftrightarrow 3x+2=1$

$\Leftrightarrow x=-\frac{1}{3}$