Mn làm giúp mình bài 2,3 với.bài 2 là chứng minh Ma//Eb//NC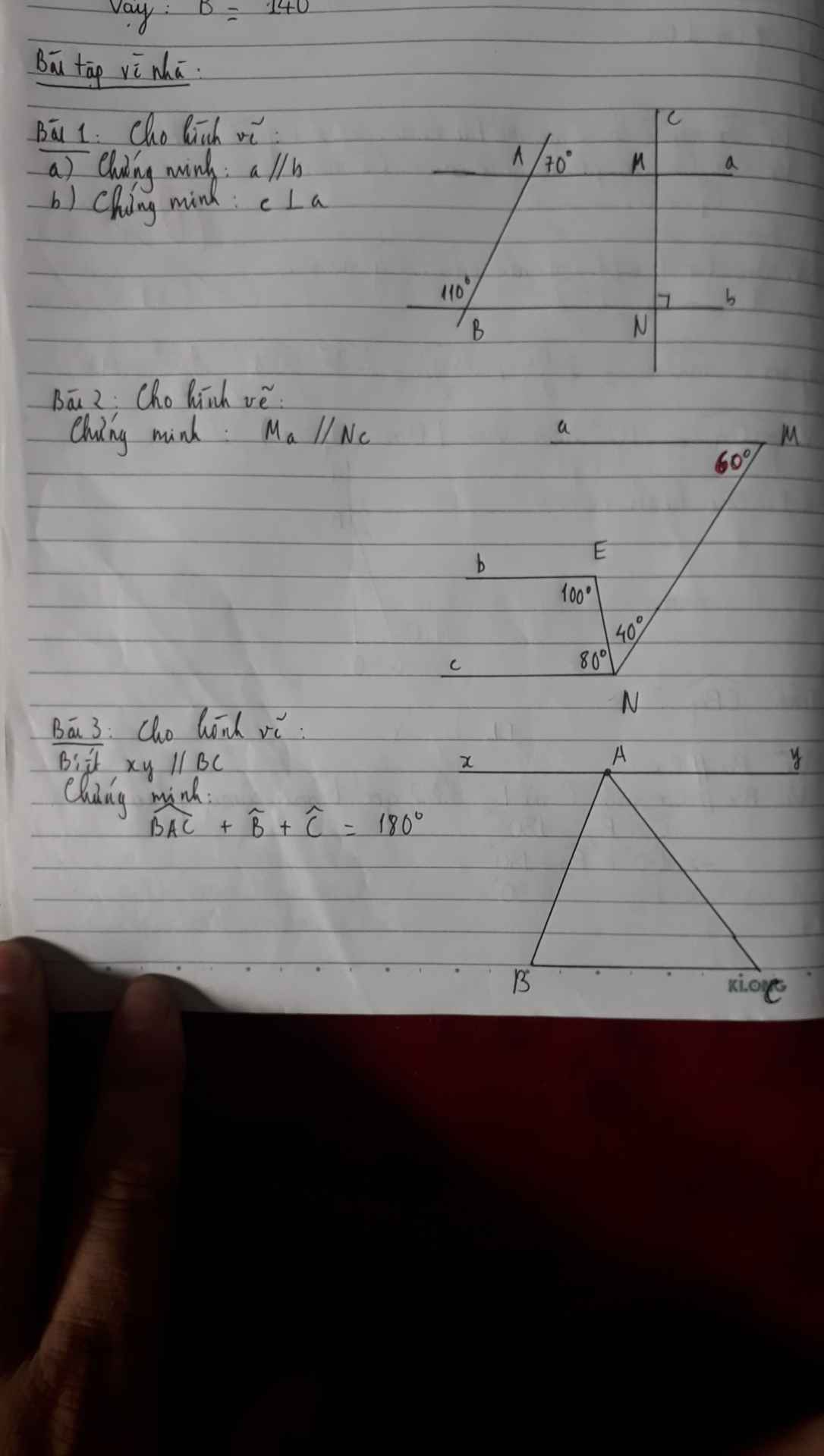

Những câu hỏi liên quan
Cho tam giác ABC có M là trung điểm của BC. Trên tia đối của tia MA lấy điểm N sao cho MN=MA. a) Chứng minh: ∆AMC=∆NMB b) Chứng minh: AC//BN c) Chứng minh: AB//NC Giúp mình với. Cảm ơn nhiều 🤩
b: Xét tứ giác ABNC có
M là trung điểm của AN
M là trung điểm của BC
Do đó: ABNC là hình bình hành
Suy ra: AC//BN
Đúng 1
Bình luận (1)
a) Xét ∆AMC và ∆NMB có:
+ AM = NM (gt).
+ Góc AMC = Góc NMB (đối đỉnh).
+ CM = BM (M là trung điểm của BC).
=> ∆AMC = ∆NMB (c - g - c).
b) ∆AMC = ∆NMB (cmt).
=> Góc CAM = Góc BNM (cặp góc tương ứng).
Mà 2 góc này ở vị trí so le trong.
=> AC // BN (dhnb).
c) ∆AMC = ∆NMB (cmt).
=> AC = NB (cặp cạnh tương ứng).
Xét tứ giác ACNB có:
+ AC = BN (cmt).
+ AC // BN (cmt).
=> Tứ giác ACNB là hình bình hành (dhnb).
=> AB // NC (tính chất hình bình hành).
Đúng 0
Bình luận (0)
1. Cho hàm số y f(x)-2x^2+1. Tìm x để f(x)- 7. 2. x /6 y / 11 và x + 15 y.Tìm x,y. 3. Cho tam giác ABC, E là trung điểm của AC. Trên tia đối của tia EB lấy điểm M sao cho EM EB a. Chứng minh tam giác AEM bằng tam giác CEB. b. Chứng minh AM song song với BC .c. Trên tia MA lấy điểm N sao cho A là trung điểm của MN . Vẽ CN cắt AB tại F. Chứng minh F là trung điểm của CN. Giúp mình với. Thanks!
Đọc tiếp
1. Cho hàm số y =f(x)=-2x^2+1. Tìm x để f(x)=- 7. 2. x /6 = y / 11 và x + 15 = y.Tìm x,y. 3. Cho tam giác ABC, E là trung điểm của AC. Trên tia đối của tia EB lấy điểm M sao cho EM = EB a. Chứng minh tam giác AEM bằng tam giác CEB. b. Chứng minh AM song song với BC .c. Trên tia MA lấy điểm N sao cho A là trung điểm của MN . Vẽ CN cắt AB tại F. Chứng minh F là trung điểm của CN. Giúp mình với. Thanks!
Bài 3:
a: Xét ΔAEM và ΔCEB có
EA=EC
\(\widehat{AEM}=\widehat{CEB}\)
EM=EB
Do đó: ΔAEM=ΔCEB
b: Xét tứ giác ABCM có
E là trung điểm của AC
E là trung điểm của BM
Do đó: ABCM là hình bình hành
Suy ra: AM//BC
Đúng 0
Bình luận (0)
a: Xét ΔAEM và ΔCEB có
EA=EC
ˆAEM=ˆCEB
EM=EB
Do đó: ΔAEM=ΔCEB
b: Xét tứ giác ABCM có
E là trung điểm của AC
E là trung điểm của BM
Do đó: ABCM là hình bình hành
Suy ra: AM//BC
Đúng 0
Bình luận (0)
CHo tam giác ABC, M là trung điểm của BC. Trên tia đối cuat tia MA, lấy điểm E sao cho ME=MA
CMR:
a)Chứng minh rằng AC//BE
b) Gọi I là một điểm trên AC, K là một điểm trên EB sao cho AI=EK. Chứng minh 3 điểm I,M,K thẳng hàng
( câu a mình biết làm rồi còn câu b giúp mình nha)
Cho tam giác ABC có M là trung điểm của BC. Trên tia đối của tia MA lấy điểm N sao cho MN=MA. a) Chứng minh: ∆AMC=∆NMB b) Chứng minh: AC//BN c) Chứng minh: AB//NC
a) Xét ∆AMC và ∆NMB có:
+ AM = NM (gt).
+ Góc AMC = Góc NMB (đối đỉnh).
+ CM = BM (M là trung điểm của BC).
=> ∆AMC = ∆NMB (c - g - c).
b) ∆AMC = ∆NMB (cmt).
=> Góc CAM = Góc BNM (cặp góc tương ứng).
Mà 2 góc này ở vị trí so le trong.
=> AC // BN (dhnb).
c) ∆AMC = ∆NMB (cmt).
=> AC = NB (cặp cạnh tương ứng).
Xét tứ giác ACNB có:
+ AC = BN (cmt).
+ AC // BN (cmt).
=> Tứ giác ACNB là hình bình hành (dhnb).
=> AB // NC (tính chất hình bình hành).
Đúng 1
Bình luận (0)
cho tam giác ABC cân tại A gọi M là trung điểm của BC. Trên Tia đối MA lấy điểm N sao cho MA=MN chứng minh AB//NC chứng minh tam giác ABN cân
Xét tứ giác ABNC có
M là trung điểm chung của AN và BC
AB=AC
=>ABNC là hình bình hành
=>BN=AC=AB
=>ΔBAN cân tạiB
Đúng 0
Bình luận (1)
Xét \(\Delta AMB\) và \(\Delta NMC\) có :
\(\widehat{AMB}=\widehat{NMC}\) ( đối đỉnh )
AM = NM ( gt )
MB = MC ( M là trung điểm của BC )
\(\Rightarrow\Delta AMB=\Delta NMC\) ( c.g.c )
\(\Rightarrow\widehat{BAM}=\widehat{CNM}\) ( 2 góc tương ứng )
mà 2 góc này ở vị trí so le trong
\(\Rightarrow AB//NC\) (đpcm)
Xét \(\Delta AMCvà\Delta NMBcó\) :
\(\widehat{AMC}=\widehat{NMB}\) ( đối đỉnh )
AM = NM ( gt )
MC = MB ( M là trung điểm của BC )
\(\Rightarrow\Delta AMC=\Delta NMB\) ( c.g.c )
Xét \(\Delta AMBvà\Delta AMCcó\) :
AM chung
MB = MC ( M là trung điểm của BC )
AB = AC (\(\Delta ABC\) cân tại A )
\(\Rightarrow\Delta AMB=\Delta AMC\) ( c.c.c )
mà \(\Delta NMB=\Delta AMC\)
\(\Rightarrow\Delta AMB=\Delta NMB\) ( tính chất bắc cầu )
\(\Rightarrow BA=BN\) ( 2 cạnh tương ứng )
\(\Rightarrow\Delta ABN\) cân tại B ( đpcm )
Đúng 0
Bình luận (0)
Giải giúp em bài này với, em cảm ơn anh chị nhiều lắm ạ! Bài 4. Cho tam giác ABC, điểm M là trung điểm BC. Trên tia đối của tia MA lấy N sao cho MN=MA. a) Chứng minh AB = CN b) Chứng minh AB+AC > 2.AM
a: Xét tứ giác ABNC có
M là trung điểm của AN và BC
=>ABNC là hình bình hành
=>AB=CN
b: AB+AC=CN+AC>NC=2AM
Đúng 1
Bình luận (0)
Cho hình tam giác ABC có AM=MN=NC=AC/3;AE=EB=AB/2;BI=IN=BN/2 và diện tích của hình tam giác ABC bằng 1200 cm vuông.tính diện tích hình EMNI
Làm ơn giúp mình giải chi tiết với, mình sẽ tick cho.
chịa quá dài so với tưởng tượng
Làm giúp mình bài này với (T^T)
Cho tam giác ABC có AC>AB, trung tuyến AM. Trên tia đối của tia MA lấy điểm D sao cho MD=MA, nối C với D
a)Chứng minh góc ADC>góc DAC, từ đó suy ra góc MAB> góc MAC
b)Kẻ đường cao AH, gọi E là một điểm nằm giữa A và H. So sánh HC và HB; EC và EB
Bài 2 Cho tam giác nhọn ABC (AB < AC). Gọi M là trung điểm của BC. Trên tiađối của tia MA lấy điểm D sao cho MD MA.a) Chứng minh ABM DCM.b) Kẻ AH vuông góc với BC (H BC). Vẽ điểm E sao cho H là trung điểmcủa EA. Chứng minh BE CD.Bài 3: . Cho ΔABC có AB AC và D là trung điểm của BC. Gọi E là trung điểmcủa AC, trên tia đối của tia EB lấy điểm M sao cho EM EB.a) Chứng minh ΔABD ΔACDb) Chứng minh rằng AM 2.BDc) Tính số đo của ·MAD GIÚP EM VS BÀ CON ƠI
Đọc tiếp
Bài 2 Cho tam giác nhọn ABC (AB < AC). Gọi M là trung điểm của BC. Trên tia
đối của tia MA lấy điểm D sao cho MD = MA.
a) Chứng minh ABM = DCM.
b) Kẻ AH vuông góc với BC (H BC). Vẽ điểm E sao cho H là trung điểm
của EA. Chứng minh BE = CD.
Bài 3: . Cho ΔABC có AB = AC và D là trung điểm của BC. Gọi E là trung điểm
của AC, trên tia đối của tia EB lấy điểm M sao cho EM = EB.
a) Chứng minh ΔABD = ΔACD
b) Chứng minh rằng AM = 2.BD
c) Tính số đo của ·MAD
GIÚP EM VS BÀ CON ƠI
kékduhchchdjjdjkékduhchchdjjdjkékduhchchdjjdjkékduhchchdjjdjkékduhchchdjjdj


















