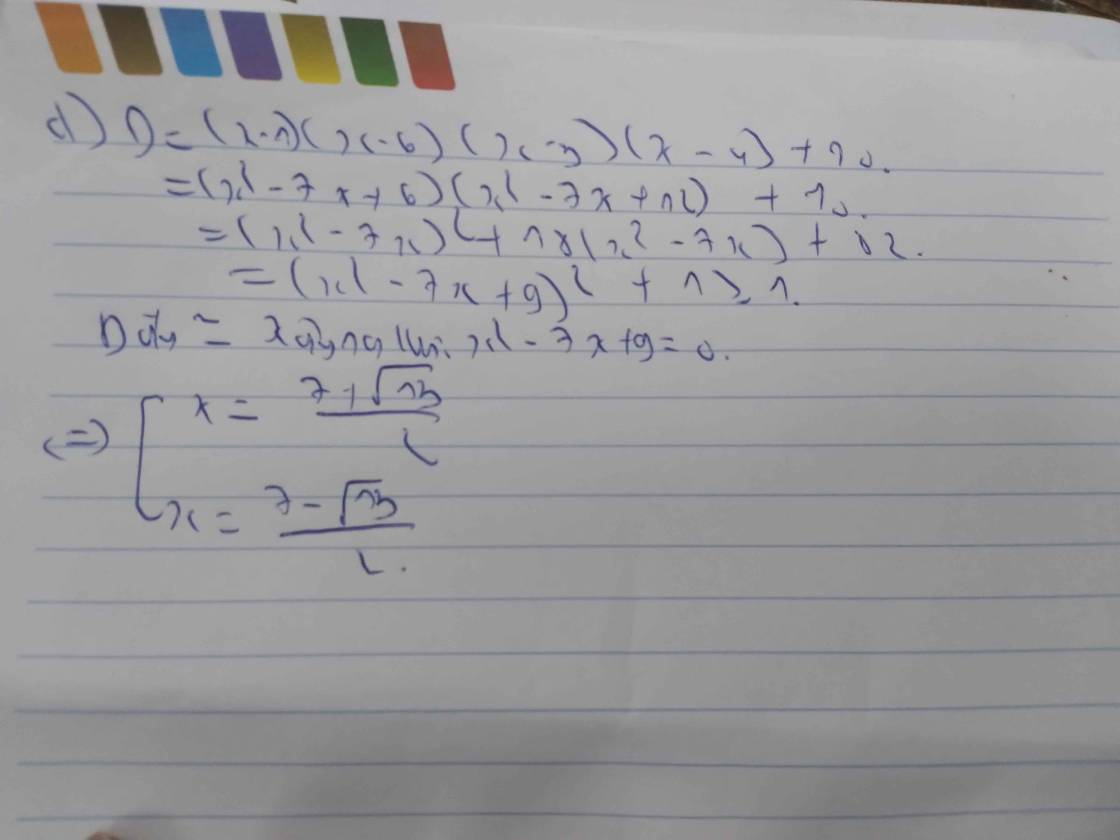nhầm đề ak

Xin phép được sủa đề một chút nhé :)

\(\left\{{}\begin{matrix}x+y=z=a\\x^2+y^2+z^2=b\\a^2=b+4034\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x^2+y^2+z^2+2\left(xy+yz+zx\right)=a^2\\x^2+y^2+z^2=b\\a^2-b=4034\end{matrix}\right.\)

\(\Leftrightarrow\left\{{}\begin{matrix}a^2-b=2\left(xy+yz+zx\right)\\a^2-b=4034\end{matrix}\right.\Leftrightarrow xy+yz+zx=2017\)

\(M=x\sqrt{\frac{\left(2017+y^2\right)\left(2017+z^2\right)}{2017+x^2}}+y\sqrt{\frac{\left(2017+x^2\right)\left(2017+z^2\right)}{2017+y^2}}+z\sqrt{\frac{\left(2017+y^2\right)\left(2017+x^2\right)}{2017+z^2}}\)

\(=x\sqrt{\frac{\left(x+y\right)\left(y+z\right)\left(y+z\right)\left(z+x\right)}{\left(x+y\right)\left(z+x\right)}}+y\sqrt{\frac{\left(x+y\right)\left(z+x\right)\left(y+z\right)\left(z+x\right)}{\left(x+y\right)\left(y+z\right)}}+z\sqrt{\frac{\left(x+y\right)\left(z+x\right)\left(x+y\right)\left(y+z\right)}{\left(y+z\right)\left(z+x\right)}}\)

\(=2\left(xy+yz+zx\right)=4034\)

Đặt \(g\left(x\right)=\left(1+x\right)\left(2+x\right)...\left(2017+x\right)\)

\(\Rightarrow g\left(0\right)=1.2.3...2017=2017!\)

\(f\left(x\right)=\dfrac{x}{g\left(x\right)}\Rightarrow f'\left(x\right)=\dfrac{g\left(x\right)-x.g'\left(x\right)}{g^2\left(x\right)}\)

\(\Rightarrow f'\left(0\right)=\dfrac{g\left(0\right)-0.g'\left(x\right)}{\left[g\left(0\right)\right]^2}=\dfrac{g\left(0\right)}{\left[g\left(0\right)\right]^2}=\dfrac{1}{g\left(0\right)}=\dfrac{1}{2017!}\)

Ta có :   \(\left(x+\sqrt{x^2+2017}\right)\left(-x+\sqrt{x^2+2017}\right)=2017\left(1\right)\)

    \(\left(y+\sqrt{y^2+2017}\right)\left(-y+\sqrt{y^2+2017}\right)=2017\left(2\right)\)

        nhân theo vế của ( 1 ) ; ( 2 ) , ta có :

     \(2017\left(-x+\sqrt{x^2+2017}\right)\left(-y+\sqrt{y^2+2017}\right)=2017^2\)

    \(\Rightarrow\left(-x+\sqrt{x^2+2017}\right)\left(-y+\sqrt{y^2+2017}\right)=2017\)

  rồi bạn nhân ra , kết hợp với việc nhân biểu thức ở phần trên xong cộng từng vế , cuối cùng ta đc :

     \(xy+\sqrt{\left(x^2+2017\right)\left(y^2+2017\right)}=2017\)

     \(\Leftrightarrow\sqrt{\left(x^2+2017\right)\left(y^2+2017\right)}=2017-xy\)

     \(\Leftrightarrow x^2y^2+2017\left(x^2+y^2\right)+2017^2=2017^2-2\cdot2017xy+x^2y^2\) 

       \(\Rightarrow x^2+y^2=-2xy\Rightarrow\left(x+y\right)^2=0\Rightarrow x=-y\)

  A = 2017 

 ( phần trên mk lười nên không nhân ra, bạn giúp mk nhân ra nha :)   )

2/ \(\frac{\sqrt{x-2011}-1}{x-2011}+\frac{\sqrt{y-2012}-1}{y-2012}+\frac{\sqrt{z-2013}-1}{z-2013}=\frac{3}{4}\)

\(\Leftrightarrow\frac{4\sqrt{x-2011}-4}{x-2011}+\frac{4\sqrt{y-2012}-4}{y-2012}+\frac{4\sqrt{z-2013}-4}{z-2013}=3\)

\(\Leftrightarrow\left(1-\frac{4\sqrt{x-2011}-4}{x-2011}\right)+\left(1-\frac{4\sqrt{y-2012}-4}{y-2012}\right)+\left(1-\frac{4\sqrt{z-2013}-4}{z-2013}\right)=0\)

\(\Leftrightarrow\left(\frac{x-2011-4\sqrt{x-2011}+4}{x-2011}\right)+\left(\frac{y-2012-4\sqrt{y-2012}+4}{y-2012}\right)+\left(\frac{z-2013-4\sqrt{z-2013}+4}{z-2013}\right)=0\)

\(\Leftrightarrow\frac{\left(\sqrt{x-2011}-2\right)^2}{x-2011}+\frac{\left(\sqrt{y-2012}-2\right)^2}{y-2012}+\frac{\left(\sqrt{z-2013}-2\right)^2}{z-2013}=0\)

Dấu = xảy ra khi \(\sqrt{x-2011}=2;\sqrt{y-2012}=2;\sqrt{z-2013}=2\)

\(\Leftrightarrow x=2015;y=2016;z=2017\)

3/ \(\sqrt{\frac{1}{\left(a-b\right)^2}+\frac{1}{\left(b-c\right)^2}+\frac{1}{\left(c-a\right)^2}}\)

\(=\sqrt{\frac{\left(a-b\right)^2\left(b-c\right)^2+\left(b-c\right)^2\left(c-a\right)^2+\left(a-b\right)^2\left(c-a\right)^2}{\left(a-b\right)^2\left(b-c\right)^2\left(c-a\right)^2}}\)

\(=\sqrt{\frac{\left(a^2+b^2+c^2-ab-bc-ca\right)^2}{\left(a-b\right)^2\left(b-c\right)^2\left(c-a\right)^2}}\)

\(=|\frac{a^2+b^2+c^2-ab-bc-ca}{\left(a-b\right)\left(b-c\right)\left(c-a\right)}|\) là số hữu tỉ

Lời giải:

Ta thấy: \(f(x)=\frac{x^3}{1-3x+3x^2}\Rightarrow f(1-x)=\frac{(1-x)^3}{1-3(1-x)+3(1-x)^2}=\frac{(1-x)^3}{3x^2-3x+1}\)

\(\Rightarrow f(x)+f(1-x)=\frac{x^3}{1-3x+3x^2}+\frac{(1-x)^3}{3x^2-3x+1}=\frac{x^3+(1-x)^3}{3x^2-3x+1}=1\)

Do đó:

\(f\left(\frac{1}{2017}\right)+f\left(\frac{2016}{2017}\right)=1\)

\(f\left(\frac{2}{2017}\right)+f\left(\frac{2015}{2017}\right)=1\)

............

\(f\left(\frac{1008}{2017}\right)+f\left(\frac{1009}{2017}\right)=1\)

Cộng theo vế:

\(\Rightarrow A=f\left(\frac{1}{2017}\right)+f\left(\frac{2}{2017}\right)+f\left(\frac{3}{2017}\right)+...f\left(\frac{2015}{2017}\right)+f\left(\frac{2016}{2017}\right)\)

\(=\underbrace{1+1+1...+1}_{1008}=1008\)

Bạn xem lại đề nhé.

a) \(A=x^2+5y^2+2xy-4x-8y+2015\)

\(A=x^2-4x+4-2y\left(x-2\right)+y^2+2011+4y^2\)

\(A=\left(x-2\right)^2-2y\left(x-2\right)+y^2+2011+4y^2\)

\(A=\left(x-2-y\right)^2+4y^2+2011\)

Vì \(\left(x-y-2\right)^2\ge0;4y^2\ge0\)

\(\Rightarrow A_{min}=2011\)

Dấu bằng xảy ra : \(\Leftrightarrow\left\{{}\begin{matrix}x-y-2=0\\4y^2=0\end{matrix}\right.\Leftrightarrow}\left\{{}\begin{matrix}x=2\\y=0\end{matrix}\right.\)

b) \(B=\left(x-2012\right)^2+\left(x+2013\right)^2\)

\(B=x^2-4024x+2012^2+x^2+4026x+2013^2\)

\(B=2x^2+2x+2012^2+2013^2\)

\(B=2\left(x^2+x+\dfrac{1}{4}\right)+2012^2+2013^2-\dfrac{1}{2}\)

\(B=2\left(x+\dfrac{1}{2}\right)^2+2012^2+2013^2-\dfrac{1}{2}\)

\(\Rightarrow B_{min}=2012^2+2013^2-\dfrac{1}{2}\)

Dấu bằng xảy ra : \(\Leftrightarrow x=-\dfrac{1}{2}\)

Đặt x - 2017 = a

Phương trình trên tương đương:

\(\dfrac{\left(-a\right)^2-\left(-a\right)\left(a-1\right)+\left(a-1\right)^2}{\left(-a\right)^2+\left(-a\right)\left(a-1\right)+\left(a-1\right)^2}=\dfrac{5}{3}\)

\(\Leftrightarrow\dfrac{a^2+a^2-a+a^2-2a+1}{a^2-a^2+a+a^2-2a+1}=\dfrac{5}{3}\)

\(\Leftrightarrow\dfrac{3a^2-3a+1}{a^2-a+1}=\dfrac{5}{3}\)

\(\Leftrightarrow9x^2-9x+3=5x^2-5x+5\)

\(\Leftrightarrow4x^2-4x-2=0\)

\(\Leftrightarrow\left(x-\dfrac{1+\sqrt{3}}{2}\right)\left(x-\dfrac{1-\sqrt{3}}{2}\right)=0\)

\(\Leftrightarrow\left[{}\begin{matrix}\dfrac{1+\sqrt{3}}{2}\\\dfrac{1-\sqrt{3}}{2}\end{matrix}\right.\)

Vậy tập nghiệm của phương trình: \(S=\left\{\dfrac{1+\sqrt{3}}{2};\dfrac{1-\sqrt{3}}{2}\right\}\)

À khác cái dấu nhưng đề phải là giải phương trình chứ
Đặt 2017-x=a => x-2018=-a-1 phương trình trở thành:
\(\frac{a^2+a\left(-a-1\right)+\left(a-1\right)^2}{a^2-a\left(-a-1\right)+\left(a-1\right)^2}=\frac{19}{49}\)
\(\Leftrightarrow\frac{a^2+a+1}{3a^2+3a+1}=\frac{19}{49}\)
\(\Leftrightarrow49\left(a^2+a+1\right)=19\left(3a^2+3a+1\right)\)

\(\Leftrightarrow49a^2+49a+49=57a^2+57a+19\)

\(\Leftrightarrow8a^2+8a-30=0\)

\(\Leftrightarrow\orbr{\begin{cases}a=\frac{3}{2}\\a=-\frac{5}{2}\end{cases}\Rightarrow\orbr{\begin{cases}x=2015,5\\x=2019,5\end{cases}}}\)
Vậy......................

Tử và mẫu giống nhau mà