vẽ hình chópS.ABCD đều có AB=8cm cạnh bên C=20cm. tính chiều cao SH,Sxq,STP của hình chóp

Những câu hỏi liên quan
cho hình chóp đều có S.ABCD có đáy là 12cm , chiều cao là 8cm . tính sxq,stp,v
vẽ hình chóp S.ABC đều có AB=3cm, cạnh bên SC=8cm
tính chiều cao SH, Sxq, Stp của hình chóp
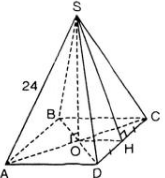
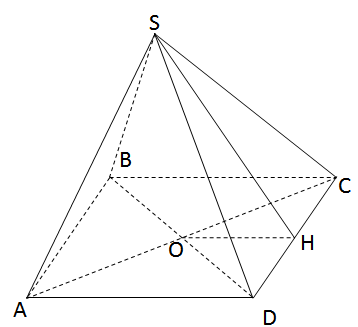
Cho hình chóp tứ giác đều S.ABCD có cạnh đáy AB = 20cm, cạnh bên SA = 24cm.
a) Tính chiều cao SO rồi tính thể tích của hình chóp.
b) Tính diện tích toàn phần của hình chóp.
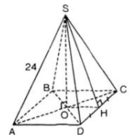
a) S.ABCD là hình chóp tứ giác đều
⇒ ABCD là hình vuông
⇒ AC = AB√2 = 20√2 (cm).
SO là chiều cao của hình chóp
⇒ O = AC ∩ BD và SO ⊥ (ABCD)
⇒ SO ⊥ AO
⇒ ΔSAO vuông tại O
⇒ SO2 + OA2 = SA2
⇒ SO2 = SA2 – OA2 = SA2 – (AC/2)2 = 242 - 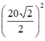 = 376
= 376
⇒ SO = √376 ≈ 19,4 (cm).
Thể tích hình chóp:
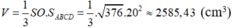
b) Gọi H là trung điểm của CD
SH2 = SD2 – DH2 = 242 – 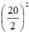 = 476
= 476
⇒ SH = √476 ≈ 21,8 (cm)
⇒ Sxq = p.d = 2.AB.SH = 2.20.√476 ≈ 872,7 (cm2 ).
Sđ = AB2 = 202 = 400 (cm2 )
⇒ Stp = Sxq + Sđ = 872,7 + 400 = 1272,7 (cm2 ).
Đúng 0
Bình luận (0)
cho hình lăng trụ đứng tam giác đề abc . a'b'c' có cạnh đáy = 12cm chiều cao aa'=8cm tính Sxq ,Stp,V lăng trụ ( có hình vẽ nha)
cho hình chóp đều SABC có cạnh đáy là 6, chiều cao là 4. tính trung đoạn và Sxq, Stp và thể tích.
Hình chóp tam giác đều tất cả 4 mặt đều là tam giác đều
\(S_{xq}=3.S_{1mạt}=3\cdot\frac{1}{2}\cdot6\cdot\frac{6\sqrt{3}}{2}=27\sqrt{3}\)
\(S_{tp}=4S_{1mat}=4\cdot9\sqrt{3}=36\sqrt{3}\)
\(V=\frac{1}{3}h\cdot S_{1mat}=\frac{1}{3}\cdot4\cdot9\sqrt{3}=12\sqrt{3}\left(đvtt\right)\)
Đúng 0
Bình luận (0)
cho hình chóp tứ giác đều S.ABCD có cạnh đáy AB=20cm, cạnh bên SA=24 cm.
a) Tính chiều cao SO rồi tính thể tích hình chóp đều
b) Tính diienj tích toàn phần của hình chóp
Cho hình chóp tứ giác đều S.ABCD có cạnh đáy AB = 20cm, cạnh bên SA = 24cm
a) Tính chiều cao SO rồi tính thể tích của hình chóp
b) Tính diện tích toàn phần của hình chóp
Cho hình chóp tứ giác đều S.ABCD có cạnh đáy AB = 20cm, cạnh bên SA = 24cm.
a) Tính chiều cao SO rồi tính thể tích của hình chóp.
b) Tính diện tích toàn phần của hình chóp.
a) S.ABCD là hình chóp tứ giác đều
⇒ ABCD là hình vuông
⇒ AC = AB√2 = 20√2 (cm).
SO là chiều cao của hình chóp
⇒ O = AC ∩ BD và SO ⊥ (ABCD)
⇒ SO ⊥ AO
⇒ ΔSAO vuông tại O
⇒ SO2 + OA2 = SA2
\(\Rightarrow SO^2=SA^2-OA^2=SA^2-\left(\frac{AC}{2}\right)^2=24^2-\left(\frac{20\sqrt{2}}{2}\right)^2=376\)
⇒ SO = √376 ≈ 19,4 (cm).
Thể tích hình chóp :
\(V=\frac{1}{2}SO.S_{ABCD}=\frac{1}{3}.\sqrt{376}.20^2\approx2585,43\left(cm^3\right)\)
b) Gọi H là trung điểm của CD
\(SH^2=SD^2-DH^2=24^2-\left(\frac{20}{2}\right)^2=476\)
⇒ SH = √476 ≈ 21,8 (cm)
⇒ Sxp = p.d = 2.AB.SH = 2.20.√476 ≈ 872,7 (cm2 ).
Sđ= AB2 = 202 = 400 (cm2 )
⇒ Stq = Sxq + Sđ = 872,7 + 400 = 1272,7 (cm2 ).
Cho hình chóp tứ giác đều S.ABCD có cạnh đáy AB = 20cm, cạnh bên SA = 24cm.
a) Tính chiều cao SO rồi tính thể tích của hình chóp.
b) Tính diện tích toàn phần của hình chóp.
Hướng dẫn làm bài:
a) SO2=SD2−OD2=242−(20√22)2=376SO2=SD2−OD2=242−(2022)2=376
= > SO≈19,4(cm)SO≈19,4(cm)
V=13.202.19,4≈2586,6V=13.202.19,4≈2586,6 (cm2)
b)Gọi H là trung điểm của CD.
SH2=SD2−DH2=242−(202)2=476SH2=SD2−DH2=242−(202)2=476
=>SH ≈ 21,8 (cm)
Sxq≈12.80.21,8≈872Sxq≈12.80.21,8≈872 (cm2)
Sd=AB2=202=400(cm2)Sd=AB2=202=400(cm2)
Nên Stp=Sxq+Sd=872+2.400=1672(cm)2
Đúng 0
Bình luận (0)
http://loigiaihay.com/bai-11-trang-133-sgk-toan-8-tap-2-c43a25598.html
Đúng 0
Bình luận (0)