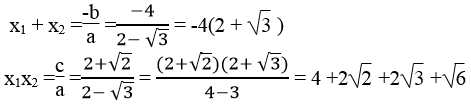Giải pt b) 2x2-5x2+3x=0

Những câu hỏi liên quan
Giải pt bằng delta và tìm nghiệm:
a) 2x2 - 5x + 1 = 0
b) 4x2 + 4x + 1 =0
c) 5x2 - x + 2 =0
a) \(2x^2-5x+1=0\)
\(\Delta=b^2-4ac\Rightarrow\left(-5\right)^2-4.2.1=17>0\)
Phương trình có 2 nghiệm phân biệt:
\(x_1=\dfrac{-b+\sqrt{\Delta}}{2a}=\dfrac{-\left(-5\right)+\sqrt{17}}{2.2}=\dfrac{5+\sqrt{17}}{4}\)
\(x_2=\dfrac{-b-\sqrt{\Delta}}{2a}=\dfrac{-\left(-5\right)-\sqrt{17}}{2.2}=\dfrac{5-\sqrt{17}}{4}\)
___________________________________________________
b) \(4x^2+4x+1=0\)
\(\Delta=b^2-4ac\Rightarrow4^2-4.4.1=0\)
Vậy phương trình có nghiệm kép:
___________________________________________________
c) \(5x^2-x+2=0\)
\(\Delta=b^2-4a\Rightarrow\left(-1\right)^2-4.5.2=-39\)
Vậy phương trình vô nghiệm.
Đúng 2
Bình luận (2)
\(a,2x^2-5x+1=0\)
\(\Delta=-b^2-4ac\)
\(\Delta=25-8\)
\(\Delta=17\)
Vậy phương trình có `2` nghiệm phân biệt :
\(x_1=\dfrac{-b+\sqrt{\Delta}}{2a}=\dfrac{5+\sqrt{17}}{4} \)
\(x_2=\dfrac{-b-\sqrt{\Delta}}{2a}=\dfrac{5-\sqrt{17}}{4}\)
\(b,4x^2+4x+1=0\)
\(\Delta=b^2-4ac\)
\(\Delta=16-16=0\)
Vậy phương trình có nghiệm kép :
\(x=\dfrac{-b}{2a}=-\dfrac{4}{8}=-\dfrac{1}{2}\)
\(c,5x^2-x+2=0\)
\(\Delta=1-40\)
\(\Delta=-39\)
Vậy phương trình vô nghiệm .
Đúng 0
Bình luận (0)
giúp mình bt này với ạ:a,x2-7x+13=0,b:-5x2+5x-1,25=0,C:x2-\2x-1=0,d:2x2+3x+1=0
a: x^2-7x+13=0
Δ=(-7)^2-4*1*13=49-52=-3<0
=>PTVN
b: -5x^2+5x-1.25=0
=>4x^2-4x+1=0
=>(2x-1)^2=0
=>2x-1=0
=>x=1/2
d: 2x^2+3x+1=0
=>(x+1)(2x+1)=0
=>x=-1 hoặc x=-1/2
Đúng 0
Bình luận (0)
Giải các phương trình sau:a)
3
x
+
1
−
2
x
+
2
4
x
+
5
x
2
+
3
x
+
2...
Đọc tiếp
Giải các phương trình sau:
a) 3 x + 1 − 2 x + 2 = 4 x + 5 x 2 + 3 x + 2 ;
b) 2 x 2 + x + 6 x 3 − 8 + 2 2 − x = 3 x 2 + 2 x + 4 .
Không giải phương trình, dùng hệ thức Vi-ét, hãy tính tổng và tích các nghiệm của mỗi phương trình
a.2x2 – 7x +2 =0 b.5x2 +2x -16 =0
c. (2 - √3 )x2+4x +2 +√2 =0 d.1,4x2 -3x +1,2 =0
e.5x2 +x +2 =0
a) Ta có:Δ =(-7)2 -4.2.2 =49 -16 =33 >0
Phương trình có 2 nghiệm phân biệt .Theo hệ thức Vi-ét, ta có:
x1 + x2 =-b/a =7/2 ;x1x2 =c/a =2/2 =1
b) c = -16 suy ra ac < 0
Phương trình có 2 ghiệm phân biệt .Theo hệ thức Vi-ét, ta có:
x1 + x2 =-b/a =-2/5 ;x1x2 =c/a =-16/5
c) Ta có: Δ’ = 22 – (2 -√3 )(2 + √2 ) =4 -4 - 2√2 +2√3 +√6
= 2√3 - 2√2 +√6 >0
Phương trình 2 ghiệm phân biệt .Theo hệ thức Vi-ét, ta có:
d) Ta có : Δ = (-3)2 -4.1,4.1,2 =9 – 6,72 =2,28 >0
Phương trình có 2 ghiệm phân biệt .Theo hệ thức Vi-ét, ta có:
x1 + x2 = -b/a = 3/(1.4) = 30/14 = 15/7 ; x1x2 = c/a = (1.2)/(1.4) = 12/14 = 6/7
Ta có: Δ = 12 -4.5.2 = 1 - 40 = -39 < 0
Đúng 0
Bình luận (0)
giải PT (dùng công thức nghiệm hoặc công thức nghiệm thu gọn)
a) x2+2x-30=0
b) 2x2-3x-5=0
a: \(\Delta=2^2-4\cdot1\cdot\left(-30\right)=124\)
Do đó: Phương trình có hai nghiệm phân biệt là:
\(\left\{{}\begin{matrix}x_1=\dfrac{-2-2\sqrt{31}}{2}=-1-\sqrt{31}\\x_2=-1+\sqrt{31}\end{matrix}\right.\)
b: \(2x^2-3x-5=0\)
\(\Leftrightarrow2x^2-5x+2x-5=0\)
=>(2x-5)(x+1)=0
=>x=5/2 hoặc x=-1
Đúng 0
Bình luận (0)
a.\(x^2+2x-30=0\)
\(\Delta=2^2-4.\left(-30\right)=4+120=124>0\)
=> pt có 2 nghiệm
\(\left\{{}\begin{matrix}x=\dfrac{-2+\sqrt{124}}{2}=\dfrac{-2+2\sqrt{31}}{2}=-1+\sqrt{31}\\x=\dfrac{-2-\sqrt{124}}{2}=-1-\sqrt{31}\end{matrix}\right.\)
b.\(2x^2-3x-5=0\)
Ta có: a-b+c=0
\(\Rightarrow\left\{{}\begin{matrix}x=-1\\x=\dfrac{5}{2}\end{matrix}\right.\)( vi-ét )
Đúng 0
Bình luận (0)
làm tính nhân
a) 5x2.(3x2 - 7x + 2)
b) (2x2-3x).(5x2-5x +1)
a) 5x^2. (3x^2 - 7x + 2)
= 5x^2. 3x^2 + 5x^2. (- 7x) + 5x^2. 2
= 15x^4 - 35x^3 + 10x^2
b) (2x^2 - 3x). (5x^2 - 5x + 1)
= 2x^2. 5x^2 - 2x^2. 5x + 2x^2. 1 - 3x. 5x^2 + 3x. 5x^2 + 3x. 5x - 3x. 1
= 10x^4 - 25x^3 + 17x^2 - 3x
Đúng 0
Bình luận (0)
giải pt sau:
a. (2x2 + 3)(-x + 7) = 0
b. (x2 - 2)(x+5)(-3x+8) = 0
a: =>7-x=0
hay x=7
b: \(\Leftrightarrow\left(x-\sqrt{2}\right)\left(x+\sqrt{2}\right)\left(x+5\right)\left(3x-8\right)=0\)
hay \(x\in\left\{\sqrt{2};-\sqrt{2};-5;\dfrac{8}{3}\right\}\)
Đúng 0
Bình luận (0)
giải pt sau:
a. (2x2 + 3)(-x + 7) = 0
b. (x2 - 2)(x+5)(-3x+8) = 0
a: =>-x+7=0
hay x=7
b: \(\Leftrightarrow\left(x-\sqrt{2}\right)\left(x+\sqrt{2}\right)\left(x+5\right)\left(3x-8\right)=0\)
hay \(x\in\left\{\sqrt{2};-\sqrt{2};-5;\dfrac{8}{3}\right\}\)
Đúng 0
Bình luận (0)
Bài 9.Rút gọn biểu thức
a)-5x2+3x.(x+2)
b)-2x.(1-x2)-2x3
c)4x.(x-1)-4(x2+2x-1)
d)6x3-2x2(-x2-3x)
e)3x(x-1)-(1+2x).5x
f)-5x2-(x-6).(-2x2)
Giúp mình với mn
\(a\\ -5x^2+3x.\left(x+2\right)=-5x^2+3x^2+6x=-2x^2+6x\\ b\\ -2x.\left(1-x^2\right)-2x^3=-2x+2x^3-2x^3=-2x\\ c\\ 4x.\left(x-1\right)-4.\left(x^2+2x-1\right)\\ =4x^2-4x-4x^2-8x+4=-12x+4\)
Đúng 1
Bình luận (0)
\(d\\ 6x^3-2x^2.\left(-x^2-3x\right)=6x^3+2x^4+6x^3=2x^4+12x^3\\ e\\ 3x.\left(x-1\right)-\left(1+2x\right).5x\\ =3x^2-3x-5x-10x^2=-7x^2-8x\\ f\\ -5x^2-\left(x-6\right).\left(-2x^2\right)=-5x^2+2x^3-12x^2=2x^3-17x^2\)
Đúng 1
Bình luận (0)
Bài 1. Giải các phương trình sau:
a) x2 - 6x + 5 = 0 b) 2x2 + 4x – 8 = 0
c) 4y2 – 4y + 1 = 0 d) 5x2 - x + 2 = 0
\(a,x^2-6x+5=0\\ \Rightarrow\left(x^2-5x\right)-\left(x-5\right)=0\\ \Rightarrow x\left(x-5\right)-\left(x-5\right)=0\\ \Rightarrow\left(x-1\right)\left(x-5\right)=0\\ \Rightarrow\left[{}\begin{matrix}x=1\\x=5\end{matrix}\right.\)
\(b,2x^2+4x-8=0\\ \Rightarrow x^2+2x-4=0\\ \Rightarrow\left(x^2+2x+1\right)-5=0\\ \Rightarrow\left(x+1\right)^2-\sqrt{5^2}=0\\ \Rightarrow\left(x+1+\sqrt{5}\right)\left(x+1-\sqrt{5}\right)=0\\ \Rightarrow\left[{}\begin{matrix}x=-1-\sqrt{5}\\x=-1+\sqrt{5}\end{matrix}\right.\)
\(c,4y^2-4y+1=0\\ \Rightarrow\left(2y-1\right)^2=0\\ \Rightarrow2y-1=0\\ \Rightarrow y=\dfrac{1}{2}\)
\(d,5x^2-x+2=0\)
Ta có:\(\Delta=\left(-1\right)^2-4.5.2=1-40=-39\)
Vì \(\Delta< 0\Rightarrow\) pt vô nghiệm
Đúng 0
Bình luận (0)