Cho tam giác ABC nhọn có \(\widehat{B}\) > \(\widehat{C}\). Hai đường cao BD, CE.
Cm: AC-AB>CE-BD
Những câu hỏi liên quan
Cho tam giác nhọn ABC vớ BD, CE là hai đường cao. Các điểm M,N trên cac đường thẳng CE, BD sao cho \(\widehat{AMB}=\widehat{ANC}=90^o\). Chứng minh rằng tam giác AMN cân
Cho tam giác nhọn ABC có AB AC. Hai đường cao AD và CE cắt nhau tại H. Khi đóA.widehat {HAB} widehat {HAC}. B.widehat {HAB} widehat {HAC}. C.widehat {HAB} widehat {HCB}. D.widehat {HAC} widehat {BAC}.
Đọc tiếp
Cho tam giác nhọn ABC có AB < AC. Hai đường cao AD và CE cắt nhau tại H. Khi đó
A.\(\widehat {HAB} = \widehat {HAC}\).
B.\(\widehat {HAB} > \widehat {HAC}\).
C.\(\widehat {HAB} = \widehat {HCB}\).
D.\(\widehat {HAC} = \widehat {BAC}\).
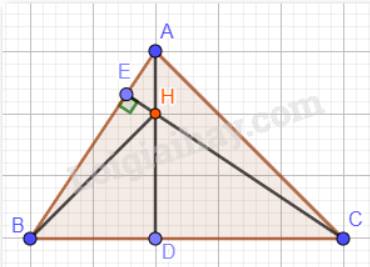
Ta có: AB < AC nên \(\widehat {ACB} < \widehat {ABC}\) (góc ACB đối diện với cạnh AB; góc ABC đối diện với cạnh AC)
Mà tam giác ADB và tam giác ADC vuông tại D.
Vì tổng hai góc nhọn trong một tam giác vuông bằng 90°.
Mà \(\widehat {ACB} < \widehat {ABC}\).
Suy ra: \(90^\circ - \widehat {ACB} > 90^0 - \widehat {ABC}\) hay \(\widehat {DAC} > \widehat {DAB}\).
Vậy \(\widehat {HAC} > \widehat {HAB}\) hay \(\widehat {HAB} < \widehat {HAC}\).
Suy ra: A, B, D sai.
Đáp án: C.\(\widehat {HAB} = \widehat {HCB}\).
Đúng 0
Bình luận (0)
Cho tam giác nhọn ABC (AB<AC) có hai đường cao BD và CE cắt nhau tại H. Tia AH cắt BC tại K. Chứng minh rằng:
a) AK⊥BC và BH.BD=BK.BC
b) \(\widehat{AED}\)=\(\widehat{ACB}\)
c) Gọi P là giao điểm của AK và DE, Q là giao điểm của DE và BC. Chứng minh KP là tia phân giác của \(\widehat{DKE}\), từ đó chứng minh PD.QE=PE.QD
a: Xét ΔABC có
BD là đường cao ứng với cạnh AC
CE là đường cao ứng với cạnh AB
BD cắt CE tại H
Do đó: H là trực tâm của ΔBAC
hay AH\(\perp\)BC tại K
Xét ΔBKH vuông tại K và ΔBDC vuông tại D có
\(\widehat{HBK}\) chung
Do đó: ΔBKH\(\sim\)ΔBDC
Suy ra: \(\dfrac{BK}{BD}=\dfrac{BH}{BC}\)
hay \(BH\cdot BD=BK\cdot BC\)
Đúng 0
Bình luận (0)
1. Cho tam giác nhọn ABC hai đường cao BD và CE cắt nhau tại H. M ∈ HB, N ∈ HC sao cho \(\widehat{AMC}=\widehat{ANB}=90^o\). CMR AN=AM
129. Cho tam giác nhọn ABC, hai đường cao BD, CE gặp nhau tại H. Vẽ điểm K sao cho AB là trung trực của HK. Chứng minh rằng \(\widehat{KAB}=\widehat{KCB}\)
Cho tam giác ABC có AB = AC, kẻ BD vuông góc với AC và CE vuông góc với AB (D thuộc AC, E thuộc AB). Gọi O là giao điểm của BD và CE. CM:
a) BD = CE
b) Tam giác OEB = tam giác ODC
c) AO là tia p/g của \(\widehat{BAC}\)
a) tam giác ABC có AB=AC (gt)
=> BD=CE
b)BD=CE (cmt)
=> OEB=ODC
c)vì O là giao điểm BD và CE (gt)
mà OEB=ODC
=> AO là tia phân giác của BAC
Đúng 1
Bình luận (0)
giúp mình bài này nhé.!!!
Tam giác ABC nhọn, có góc B > góc C, hai đường cao BD và CE. CMR: AC-AB lớn hơn CE-BD
giúp mình bài này nhé.!!!
Tam giác ABC nhọn, có góc B > góc C, hai đường cao BD và CE. CMR: AC-AB lớn hơn CE-BD
giúp mình bài này nhé.!!!
Tam giác ABC nhọn, có góc B > góc C, hai đường cao BD và CE. CMR: AC-AB lớn hơn CE-BD