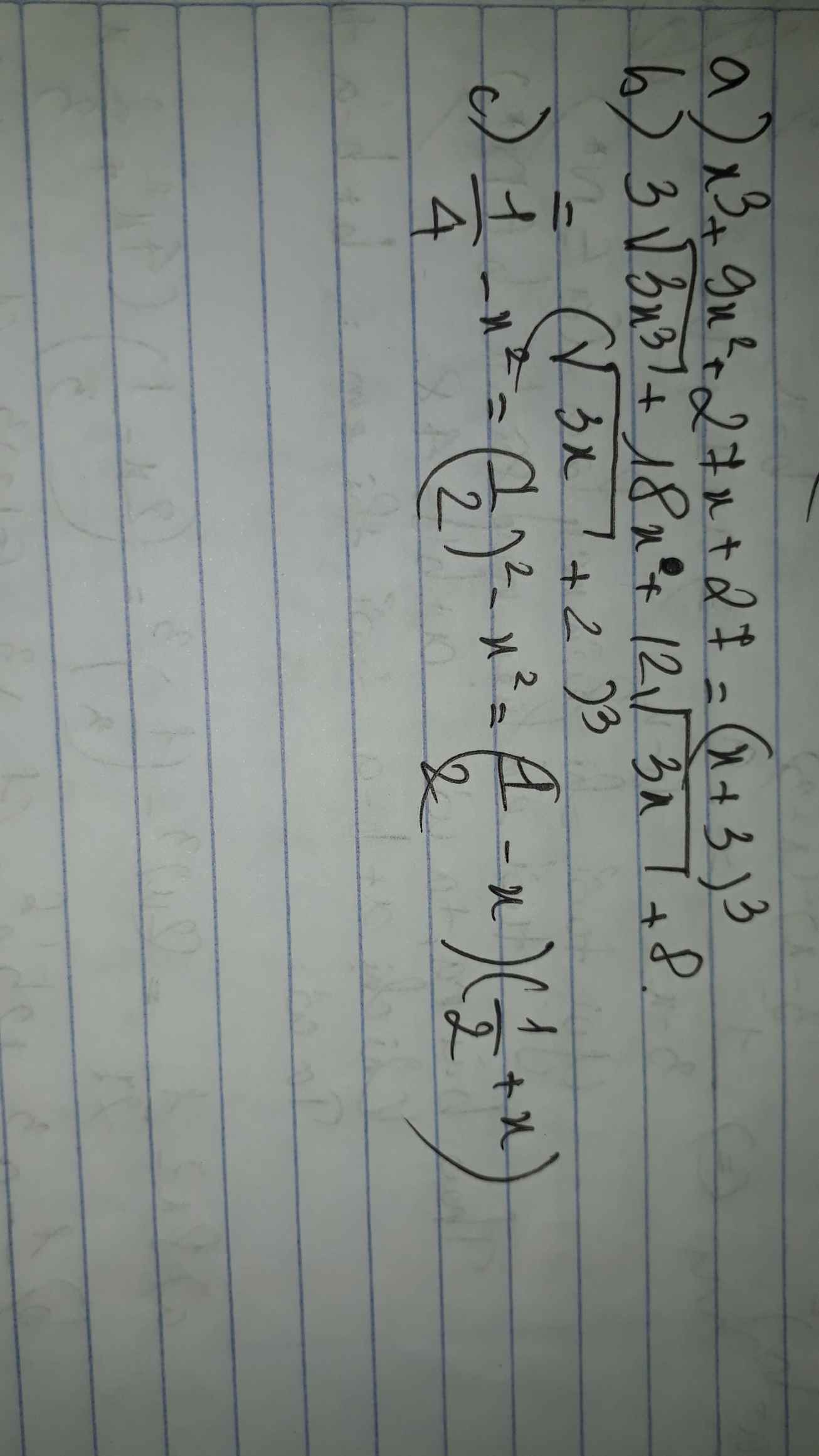Phân tích đa thức thành nhân tử : x\(\sqrt{x}\) - 3x + 4\(\sqrt{x}\) - 2 với x > 0

Những câu hỏi liên quan
Phân tích đa thức thành nhân tử \(x\sqrt{x}-3x+4\sqrt{x}-2\left(x>0\right)\)
Xem thêm câu trả lời
cách phân tích đa thức có dạng ax + b\(\sqrt{x}\) + c thành nhân tử với x > 0
từ đó phân tích đa thức x +8 \(\sqrt{x}\) + 7 thành nhân tử với x > 0
phân tích đa thức thành nhân tử
\(x\cdot\sqrt{x}-3x+4\cdot\sqrt{x}-2\) với \(x>0\)
Phân tích đa thức thành nhân tử:\(x\sqrt{x}-3x+4\sqrt{x}-2\)\(\left(x>0\right)\)
\(x\sqrt{x}-3x+4\sqrt{x}-2=x\sqrt{x}-x-2x+2\sqrt{x}+2\sqrt{x}-2\)
\(=x\left(\sqrt{x}-1\right)-2\sqrt{x}\left(\sqrt{x}-1\right)+2\left(\sqrt{x}-1\right)\)
\(=\left(\sqrt{x}-1\right)\left(x-2\sqrt{x}+2\right)\)
Phân tích đa thức thành nhân tử:
\(x\sqrt{x}-3x+4\sqrt{x}-2\) với x>0
Mong mn giúp tớ với ạ!!
CẦN GẤP!!!!!^_^
Phân tích đa thức thành nhân tử
x^3+9x^2+27x+27
3\(\sqrt{3x^3}\)+18x^2+12\(\sqrt{3x}\)+8
\(\dfrac{1}{4}\)-x^2
a) \(x^3+9x^2+27x+27=\left(x+3\right)^3\)
b) \(3\sqrt{3x^3}+18x^2+12\sqrt{3x}+8=\left(\sqrt{3x}+2\right)^3\)
c) \(\dfrac{1}{4}-x^2=\left(\dfrac{1}{2}-x\right)\left(\dfrac{1}{2}+x\right)\)
Đúng 0
Bình luận (0)
phân tích đa thức thành nhân tử
\(x+2\sqrt{x-1}\) (với x≥1)
\(x-4\sqrt{x-2}+2\) ( với x ≥2)
\(x+2\sqrt{x-1}=\left(x-1\right)+2\sqrt{x-1}+1=\left(\sqrt{x-1}+1\right)^2\)
\(x-4\sqrt{x-2}+2=\left(x-2\right)-4\sqrt{x-2}+4=\left(\sqrt{x-2}-2\right)^2\)
Đúng 1
Bình luận (0)
\(x+2\sqrt{x-1}=\left(\sqrt{x-1}+1\right)^2\)
\(x-4\sqrt{x-2}+2=\left(\sqrt{x-2}+4\right)^2\)
Đúng 0
Bình luận (0)
phân tích đa thức thành nhân tử x\(\sqrt{x}\) - 3x + 4\(\sqrt{x}\) -2 ( x > 0 )
Lời giải:
$x\sqrt{x}-3x+4\sqrt{x}-2=(x\sqrt{x}-x)-(2x-2\sqrt{x})+(2\sqrt{x}-2)$
$=x(\sqrt{x}-1)+2\sqrt{x}(\sqrt{x}-1)+2(\sqrt{x}-1)$
$=(\sqrt{x}-1)(x+2\sqrt{x}+2)$
Đúng 0
Bình luận (0)
Phân tích đa thức thành nhân tử ( với x > hoặc bằng 0 )
2+\(\sqrt{3}+\sqrt{6}+\sqrt{8}\)
\(2+\sqrt{3}+\sqrt{6}+\sqrt{8}=2+\sqrt{3}+\sqrt{6}+2\sqrt{2}\)
\(=2+\sqrt{3}+\sqrt{2}\left(2+\sqrt{3}\right)=\left(2+\sqrt{3}\right)\left(\sqrt{2}+1\right)\)
Đúng 1
Bình luận (0)
\(2+\sqrt{3}+\sqrt{6}+\sqrt{8}=\left(\sqrt{2}+1\right)\left(2+\sqrt{3}\right)\)
Đúng 0
Bình luận (0)
Phân tích đa thức thành nhân tử :
\(2x^2-3x\sqrt{x+3}+\left(x+3\right)=0\)
\(2x^2-3x\sqrt{x+3}+\left(x+3\right)\)
\(=2x^2-2x\sqrt{x+3}-x\sqrt{x+3}+\left(\sqrt{x+3}\right)^2\)
\(=2x\left(x-\sqrt{x+3}\right)-\sqrt{x+3}\left(x-\sqrt{x+3}\right)\)
\(=\left(2x-\sqrt{x+3}\right)\left(x-\sqrt{x+3}\right)\)
Đúng 0
Bình luận (0)
\(2x^2-3x\sqrt{x+3}+\left(x+3\right)\)
\(=2x^2-x\sqrt{x+3}-2x\sqrt{x+3}+\left(\sqrt{x+3}\right)^2\)
\(=x\left(2x-\sqrt{x+3}\right)-\sqrt{x+3}\left(2x-\sqrt{x+3}\right)\)
\(=\left(x-\sqrt{x+3}\right)\left(2x-\sqrt{x+3}\right)\)
Đúng 0
Bình luận (0)