a, Tìm GTNN:
M= x^2+y^2-xy-x+y+1
b, Biết xy=11 và x^2y+xy^2+x+y >Hãy tính x^2+y^2
a) phân tích đa thức thức thành nhân tử
\(x^2+2xy+7x+7y+y^2+10\)
b) biết xy=11 và \(x^2y+xy^2+x+y=2010\)
tính \(x^2+y^2\)
\(x^2+2xy+7x+7y+y^2+10\)
\(=\left(x^2+2xy+y^2\right)+\left(7x+7y\right)+\frac{49}{4}-\frac{9}{4}\)
\(=\left(x+y\right)^2+7\left(x+y\right)+\frac{49}{4}-\frac{9}{4}\)
\(=\left(x+y+\frac{7}{2}\right)^2-\frac{9}{4}\)
\(=\left(x+y+\frac{7}{2}-\frac{3}{2}\right)\left(x+y+\frac{7}{2}+\frac{3}{2}\right)\)
\(=\left(x+y+2\right)\left(x+y+5\right)\)
b)Ta có: x2y+xy2+x+y=2010
<=>xy.x+xy.y+x+y=2010
<=>11x+11y+x+y=2010
<=>12(x+y)=2010
<=>x+y=167,5
=>(x+y)2=28056,25
<=>x2+y2+2xy=28056,25
<=>x2+y2=28034,25
\(\left(x+y\right)^2+7\left(x+y\right)+\frac{49}{4}-\frac{9}{4}\)
\(=\left(x+y\right)^2+2\left(x+y\right).\frac{7}{2}+\left(\frac{7}{2}\right)^2-\frac{9}{4}\)
\(=\left(x+y+\frac{7}{2}\right)^2-\frac{9}{4}\) (áp dụng HĐT số 1)
\(=\left(x+y+\frac{7}{2}\right)^2-\left(\frac{3}{2}\right)^2\)
\(=\left(x+y+\frac{7}{2}-\frac{3}{2}\right)\left(x+y+\frac{7}{2}+\frac{3}{2}\right)\)(áp dụng HĐT số 3)
\(=\left(x+y+2\right)\left(x+y+5\right)\)
Mình cần gấp,ai giải đc thì giải hộ với!!!!!!!!!trong vòng 1h thôi!!!!!
1.tìm x;y là các số tự nhiên biết: 3x + 7y = 24
2.tìm x;y nguyên biết: x^2-4x+2y-xy+9=0
3.Cho a=b+1.Hãy rút gọn:A=(a+b)(a^2+b^2)(a^4+b^4)...(a^32+b^32)
4.Cho x,y là các số dương thỏa mãn:x^2-xy-2y^2=0.Tính A=(x^2+2011y^2):(503x^2+4y^2)
5.Cho P=(a^3-4a^2-a+4):(a^3-7a^2+14a-8)
a)Rút gọn b)Tìm a nguyên để P nguyên
1,Ta có
3x+7y=24
<=>3x=24-7y
Vì x là số tự nhiên
=>\(24-7y\ge0\)
<=>\(7y\le24\)
<=>\(y<4\) mà y là số tự nhiên
=>\(y=\left\{0;1;2;3\right\}\)
=>\(x=\left\{....\right\}\)
b,\(x^2-4x+2y-xy+9=0\)
<=>\(\left(x^2-4x+4\right)-y\left(x-2\right)+5=0\)
<=>\(\left(x-2\right)^2-y\left(x-2\right)=-5\)
<=>\(\left(x-2\right)\left(x-2-y\right)=5\)
Đến đây giải theo pp pt nghiệm nguyên.
Nếu mình làm đúng thì tick nha bạn,cảm ơn.
tick tui làm tiếp cho nha.
1. Ta có:
3x + 7y = 24
=> 24 / 3 = x ( dư 7y )
Mà 24 / 3 = 8 ( dư 0 )
Vậy x = 8 ; y = 0
Hoặc x = 1 ; y = 3.
1:Tìm GTNN x^2+y^2 biết :(x^2-y^2+1)+4x^2y^2-x^2-y^2=0
2:Cho a nhỏ hơn hoặc =a,b,c nhỏ hơn hoặc =1.Tìm GTNN,GTLN của biểu thức:P=a+b+c-ab-bc-ca
3:cho các số thực nguyên thỏa mãn điều kiện :x^2+y^2+z^2 nhỏ hơn hoặc = 27.Tìm giá trị nhỏ nhất ,GTLN x+y+z+xy+yz+zx
4: cho x,y dương thỏa mãn dk: x+y=1.Tìm GTNN:M=(x+1/x)+(y+1/y)
cho biết A=\(\frac{2}{x}\)-\(\frac{^{x^2}}{x^2+xy}\)-\(\frac{x^2-y^2}{x.y}\)-\(\frac{y^2}{x.y+y^2}\).\(\frac{x+y}{x^2+xy+y}\)
a,rút gọn A và tìm điều kiên của x,y để A xác định
b,tính gtri của A tại x=2,y=\(\frac{1}{2}\);x=1,y=1
c, tìm x \(\in\)z để A =1
Tìm x, y biết: 2/x = 3/y và xy = 96.
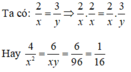
⇒ x2 = 64
⇒ x = 8 hoặc x = -8
Nếu x = 8 thì y = 96 : 8 = 12.
Nếu x = -8 thì y = 96 : (-8) = -12.
Tính giá trị biểu thức
A = (x+y)(x+2)(y+2) biết x+y= 2 và xy=-3
tks mn trc nha
Thay x+y=2 vao biểu thức A:
A=2(x+2)(y+2)
=2(xy+2x+2y+4)
=2xy +4x+4y+8
=2xy+4(x+y)+8
thay x+y=2 và xy= -3 vao A:
A= 2×(-3)+4 × 2 +8 = 10
Thay x+y=2 vào biểu thức A :
A=2(x+2)(y+2)
=2(xy+2x+2y+4)
=2xy +4x+4y+8
=2xy+4(x+y)+8
thay x+y=2 và xy= -3 vào A:
A=2 ×(-3)+4 ×2+8=10
Tìm 2 số hữu tỉ x và y (y khác 0)biết x-y=xy=x:y
Vì xy = x : y suy ra y^2 = 1 ---> y = 1 hoặc y = -1
+ Nếu y = 1 ---> x - 1 = x.1 (vô nghiệm nên tr/hợp này loại)
+ Nếu y = -1 ---> x + 1 = - x ---> 2x = -1 ---> x = -1/2 (nhận)
Vậy x = -1/2 ; y = -1.
l.anh êi , mở bài 21 trang 11 trong vở bài tập có bài này đấy
Tìm GTNN
a,\(xy+\frac{1}{xy};x,y>0;x+y\le1\)
b,S=x + 2y với hai số thực dương x,y thỏa mãn x+2y-xy=0
cS=x+2y, với 2 số thực dương x,y thỏa mãn \(x+y+xy\ge7\)
\(2\sqrt{xy}\le x+y\le1\Rightarrow\sqrt{xy}\le\frac{1}{2}\Rightarrow xy\le\frac{1}{4}\Rightarrow\frac{1}{xy}\ge4\)
\(A=xy+\frac{1}{xy}=xy+\frac{1}{16xy}+\frac{15}{16xy}\ge2\sqrt{\frac{xy}{16xy}}+\frac{15}{16}.4=\frac{17}{4}\)
\(\Rightarrow A_{min}=\frac{17}{4}\) khi \(x=y=\frac{1}{2}\)
b/ \(2y=xy-x=x\left(y-1\right)\Rightarrow x=\frac{2y}{y-1}=2+\frac{2}{y-1}\)
Đồng thời \(x;y>0\Rightarrow2y=x\left(y-1\right)>0\Rightarrow y-1>0\)
\(\Rightarrow S=2+\frac{2}{y-1}+2y=4+\frac{2}{y-1}+2\left(y-1\right)\ge4+2\sqrt{\frac{4\left(y-1\right)}{y-1}}=8\)
\(\Rightarrow S_{min}=8\) khi \(\frac{2}{y-1}=2\left(y-1\right)\Rightarrow y=2\Rightarrow x=4\)
c/ \(x+y+xy\ge7\Leftrightarrow x\left(y+1\right)\ge7-y\Leftrightarrow x\ge\frac{7-y}{y+1}=\frac{8}{y+1}-1\)
\(\Rightarrow S=x+2y\ge2y+\frac{8}{y+1}-1=2\left(y+1\right)+\frac{8}{y+1}-3\)
\(\Rightarrow S\ge2\sqrt{\frac{16\left(y+1\right)}{y+1}}-3=5\)
\(\Rightarrow S_{min}=5\) khi \(\left\{{}\begin{matrix}y=1\\x=5\end{matrix}\right.\)
Tìm số nguyên x biết
a,3x+3y-2xy=7
b,xy+2x+y+11=0
c,xy+x-y=4
d,2x.(3y-2)+(3y-2)=12
e,3x+4y-xy=15
f,xy+3x-2y=11
g,xy+12=x+y
h,xy-2x-y=-6
i,xy+4x=25+5y
ii,2xy-6y+x=9
iii,xy-x+2y=3
k,2.x^2.y-x^2-2y-2=0
l,x^2.y-x+xy=6