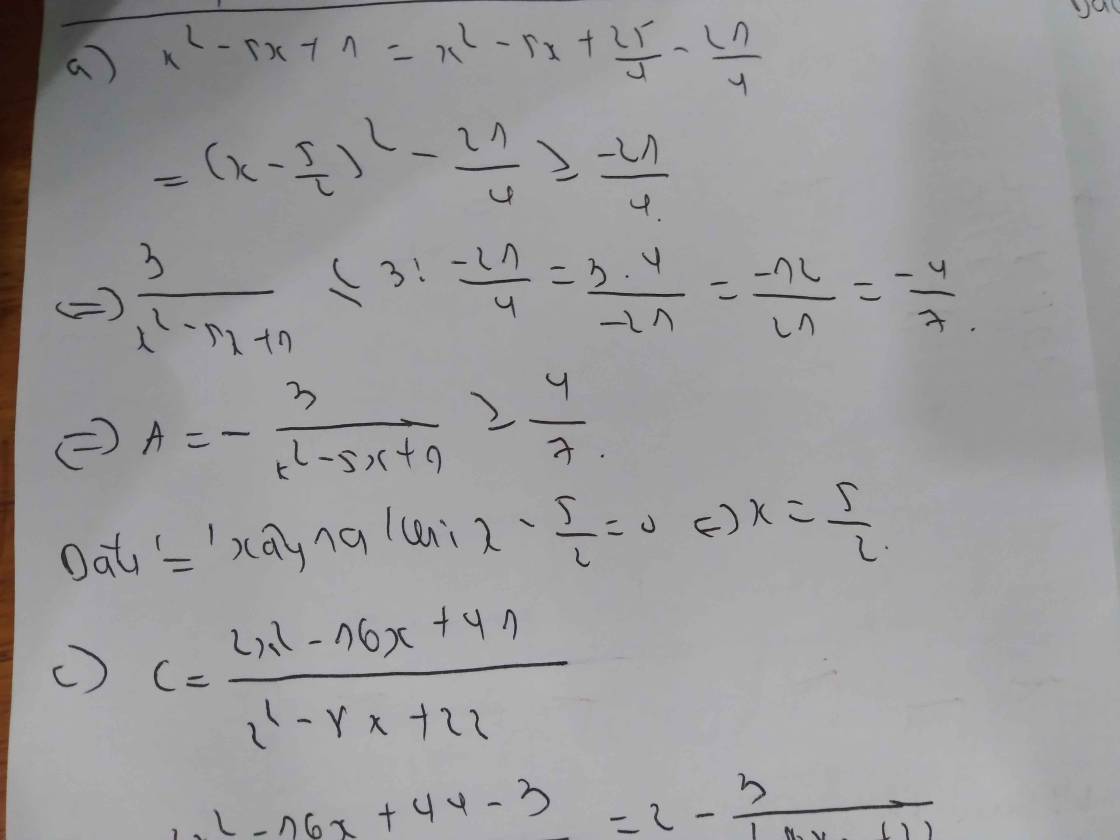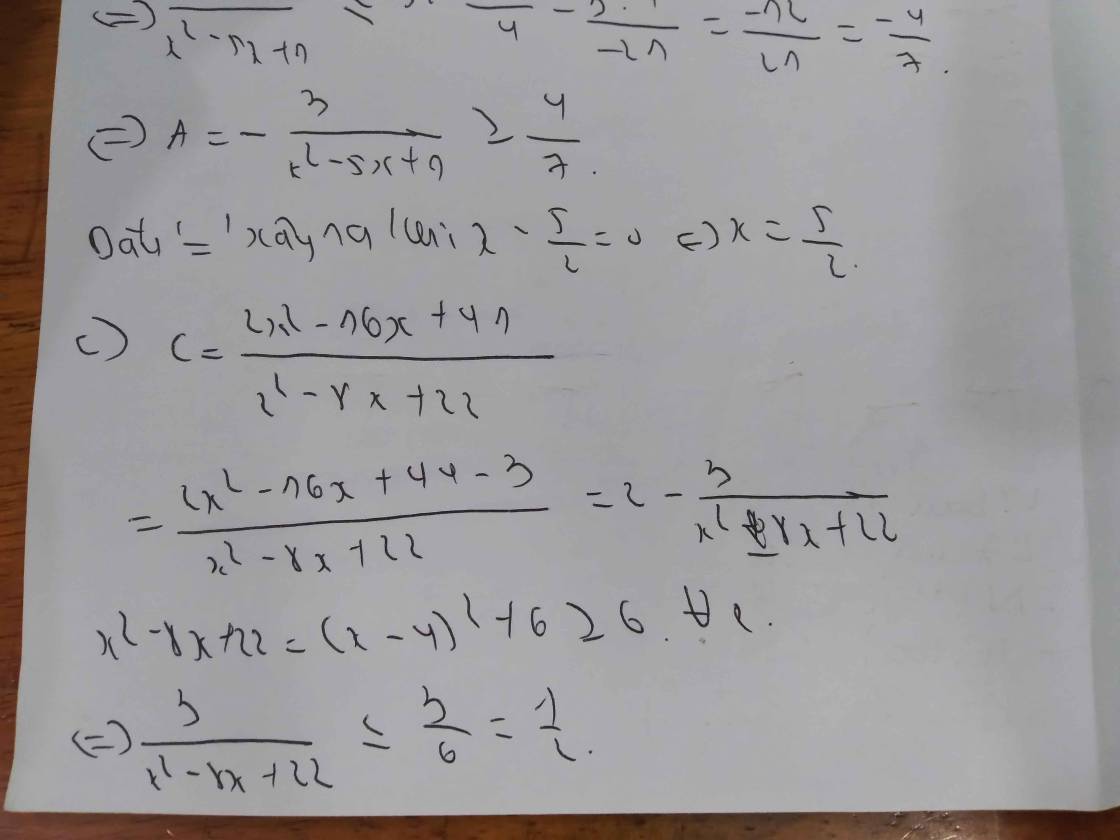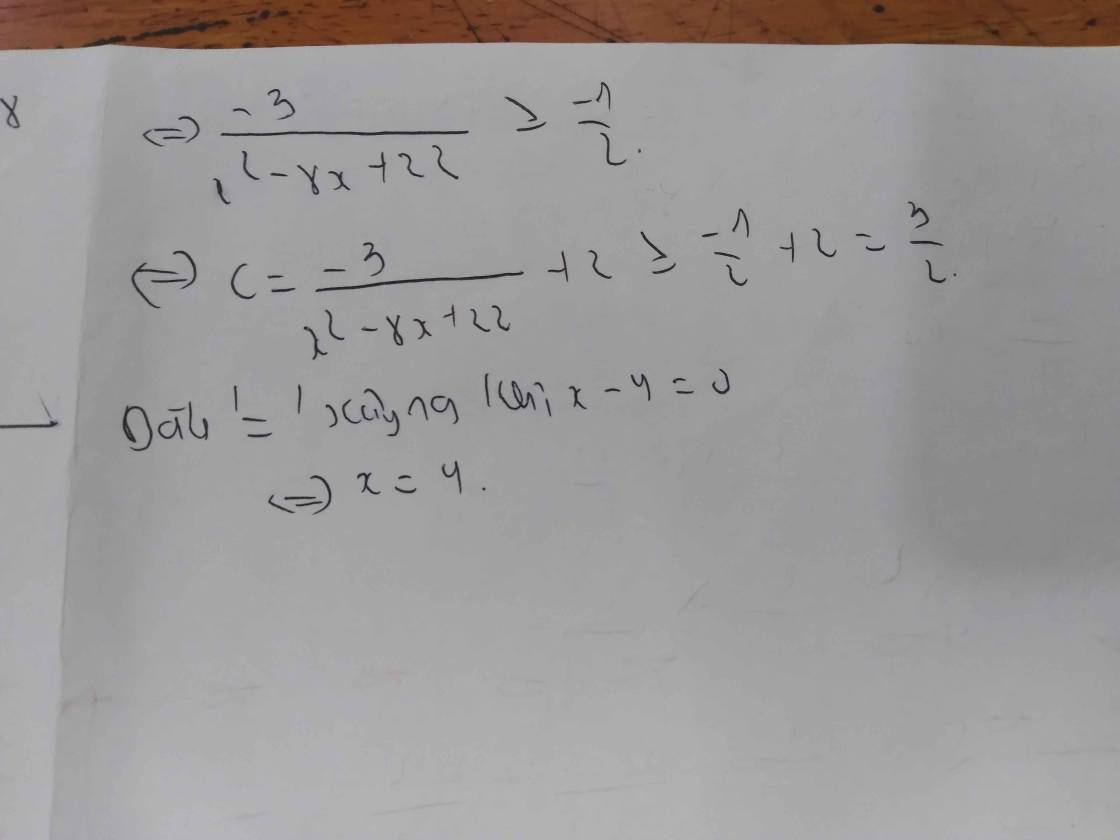tìm giá trị lớn nhất hoặc nhỏ nhất của C= 5x-x^2

Những câu hỏi liên quan
Tìm giá trị nhỏ nhất hoặc giá trị lớn nhất của đa thức sau :
-5x² + x - 7
Tìm giá trị lớn nhất (hoặc nhỏ nhất) của các biểu thức sau: C = 5 x - x 2
C = 5 x - x 2 = - x 2 - 5 x = - x 2 - 2 . 5 / 2 x + 5 / 2 2 - 5 / 2 2 = - x - 5 / 2 2 - 25 / 4 = - x - 5 / 2 2 + 25 / 4 V ì - x - 5 / 2 2 ≤ 0 ⇒ - x - 5 / 2 2 + 25 / 4 ≤ 25 / 4
Suy ra: C ≤ 25/4 .
C = 25/4 khi và chỉ khi x - 5/2 = 0 suy ra x = 5/2
Vậy C = 25/4 là giá trị lớn nhất tại x = 5/2 .
Đúng 0
Bình luận (0)
Tìm giá trị nhỏ nhất hoặc giá trị lớn nhất của các đa thức sau :
L = - 25x² + x + 3
M = - 5x² + 3x - 2
N = - 2x² + 5x + 5
Tìm giá trị lớn nhất hoặc nhỏ nhất của đa thức sau
- 5x² + x - 7
\(-5x^2+x-7=-5\left(x^2-\frac{1}{5}x+\frac{7}{5}\right)=-5\left(x^2-2\cdot\frac{1}{10}\cdot x+\frac{1}{100}-\frac{1}{100}+\frac{7}{5}\right)\)
\(=-5\left(x-\frac{1}{10}\right)^2+\frac{139}{20}\)
\(-5\left(x-\frac{1}{10}\right)^2+\frac{139}{20}\le\frac{139}{20}\)
GTLN của đa thức trên là 139/20
Đúng 0
Bình luận (0)
Tìm giá trị nhỏ nhất hoặc lớn nhất của các biểu thức sau
a) A= \(\dfrac{-3}{x^2-5x+1}\)
b) B=\(\dfrac{2x^2+4x+4}{x^2}\)
c) C= \(\dfrac{2x^2-16x+41}{x^2-8x+22}\)
Tìm giá trị lớn nhất(hoặc nhỏ nhất) của biểu thức sau
D=\(\frac{1}{x^2+5x+14}\)
\(D=\frac{1}{x^2+5x+14}=\frac{1}{\left(x^2+2.\frac{5}{2}x+\frac{5}{2}^2\right)+\frac{31}{4}}=\frac{1}{\left(x+\frac{5}{2}\right)^2+\frac{31}{4}}\le\frac{1}{\frac{31}{4}}=\frac{4}{31}\)
Dấu "=" xảy ra khi \(\left(x+\frac{5}{2}\right)^2=0\Rightarrow x=-\frac{5}{2}\)
Vậy GTLN của \(D=\frac{4}{31}\)tại \(x=-\frac{5}{2}\)
Đúng 0
Bình luận (0)
\(D=\frac{1}{x^2+5x+14}=\frac{1}{\left(x^2+2.\frac{5}{2}x+\frac{25}{4}\right)+\frac{31}{4}}=\frac{1}{\left(x+\frac{5}{2}\right)^2+\frac{31}{4}}\)
D đạt giá trị lớn nhất khi và chỉ khi \(x+\frac{5}{2}=0\leftrightarrow x=\frac{-5}{2}\)
Vậy \(D=\frac{4}{31}\leftrightarrow x=\frac{-5}{2}\)
Đúng 0
Bình luận (0)
tìm giá trị nhỏ nhất hoặc lớn nhất của đa thức sau:
2x^2-5x
tìm giá trị nhỏ nhất hoặc lớn nhất cảu các biểu thức sau:
a) A=x^2-6x+11
b)B=2x^2+10x-1
c)C=5x-x^2
\(a,A=x^2-6x+11=\left(x-3\right)^2+2\)\(\Leftrightarrow Amin=2\)
Dấu = xảy ra \(\Leftrightarrow x=3\)
Đúng 0
Bình luận (0)
\(2x^2+10x-1=2\left(x^2+5x-\frac{1}{2}\right)=2\left(x^2+2.\frac{5}{2}x+\frac{25}{4}-\frac{27}{4}\right)=2\left(x+\frac{5}{2}\right)^2-\frac{27}{2}\)
\(\Rightarrow Bmin=\frac{-27}{2}.''=''\Leftrightarrow x=\frac{-5}{2}\)
Đúng 0
Bình luận (0)
\(5x-x^2=-\left(x^2-5x\right)=-\left(x^2-2.\frac{5}{2}x+\frac{25}{4}-\frac{25}{4}\right)=-\left(x-\frac{5}{2}\right)^2+\frac{25}{4}\)\(\Leftrightarrow Cmax=\frac{25}{4}.''=''\Leftrightarrow x=\frac{5}{2}\)
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
Tìm giá trị lớn nhất hoặc nhỏ nhất
A = -2x^2 - 5x + 3
Ta có: \(A=-2x^2-5x+3\)
\(=-2\left(x^2+\dfrac{5}{2}x-\dfrac{3}{2}\right)\)
\(=-2\left(x^2+2\cdot x\cdot\dfrac{5}{4}+\dfrac{25}{16}-\dfrac{49}{16}\right)\)
\(=-2\left(x+\dfrac{5}{4}\right)^2+\dfrac{49}{8}\)
Ta có: \(\left(x+\dfrac{5}{4}\right)^2\ge0\forall x\)
\(\Rightarrow-2\left(x+\dfrac{5}{4}\right)^2\le0\forall x\)
\(\Rightarrow-2\left(x+\dfrac{5}{4}\right)^2+\dfrac{49}{8}\le\dfrac{49}{8}\forall x\)
Dấu '=' xảy ra khi \(x+\dfrac{5}{4}=0\)
hay \(x=-\dfrac{5}{4}\)
Vậy: Giá trị lớn nhất của biểu thức \(A=-2x^2-5x+3\) là \(\dfrac{49}{8}\) khi \(x=-\dfrac{5}{4}\)
Đúng 1
Bình luận (0)