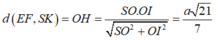Cho hình vuông ABCD có cạnh bằng a. Gọi E,F lần lượt là trung điểm của các cạnh AB,BC; M là giao điểm của CE và DF.
a) CMR: \(CE\perp DF\)
b) CMR: tam giác MAD là tam giác cân. (mình đang cần câu này...)
c) Tính diện tích tam giác MDC theo a.
Những câu hỏi liên quan
Cho hình vuông ABCD có cạnh bằng a. Gọi E;F;G;H lần lượt là trung điểm của các cạnh AB;BC;CD;DA. Gọi M là giao điểm của CE và DF. Tính diện tích tam giác MDC theo a
Xét tam giác vuông là tam giác BEC và tam giác DCF có CD = BC , BE = CF = 1/2a
=> Tam giác BEC = tam giác DCF (hai cạnh góc vuông)
=> góc CDF = góc BCE mà góc CDF + góc DFC = 90 độ
=> góc ECF + góc DFC = 90 độ hay góc DMC = 90 độ => CE vuông góc DF
Ta chứng minh được tam giác MDC đồng dạng tam giác CDF (g.g)
Áp dụng định lí Pytago có \(DF=\sqrt{CD^2+FC^2}=\sqrt{a^2+\frac{a^2}{4}}=\frac{a\sqrt{5}}{2}\)
\(S_{CDF}=\frac{1}{2}CD.CF=\frac{1}{2}a.\left(\frac{a}{2}\right)=\frac{a^2}{4}\)
Suy ra \(\frac{S_{MDC}}{S_{CDF}}=\left(\frac{CD}{DF}\right)^2=\left(\frac{a}{\frac{a\sqrt{5}}{2}}\right)^2=\left(\frac{2}{\sqrt{5}}\right)^2=\frac{4}{5}\)
\(\Rightarrow S_{MDC}=\frac{4}{5}S_{CDF}=\frac{4}{5}.\frac{a^2}{4}=\frac{a^2}{5}\)
Đúng 0
Bình luận (0)
Cho hình vuông ABCD có cạnh bằng a. Gọi E;F;G;H lần lượt là trung điểm của các cạnh AB;BC;CD;DA. Gọi M là giao điểm của CE và DF.
a) Chứng minh: EFGH là hình vuông.
b) Chứng minh: DF vuông góc CE và tam giác MAD cân
c) Tính diện tích tam giác MDC theo a
Cho hình vuông ABCD có cạnh bằng a. Gọi E, F lần lượt là trung điểm các cạnh AB,BC . Gọi M là giao điểm của CE và DF .A. c/m góc ECB = góc CDF và CE vuông góc DF B.c/m CM.CECF =a C. Gọi K là giao điểm của CM và DA . C/m tam giác MAD cân
Cho hình vuông ABCD có cạnh bằng 6 cm. Gọi E, F lần lượt là trung điểm của các cạnh AB và AD. Gấp hình vuông trên để được tứ diện ACEF. Thể tích khối tứ diện ACEF là A. 18
cm
3
. B. 3
cm
3
. C. 27
cm
3
. D. 9
cm
3
.
Đọc tiếp
Cho hình vuông ABCD có cạnh bằng 6 cm. Gọi E, F lần lượt là trung điểm của các cạnh AB và AD. Gấp hình vuông trên để được tứ diện ACEF. Thể tích khối tứ diện ACEF là
A. 18 cm 3 .
B. 3 cm 3 .
C. 27 cm 3 .
D. 9 cm 3 .
6 tháng 12 2021 lúc 16:08
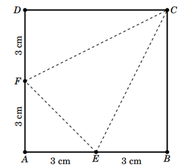
Cho hình vuông ABCD có cạnh 6cm. E,F,G,H lần lượt là trung điểm các cạnh AB,BC,CD,AD. Nối các điểm E,F,G,H thành hình vuông EFGH. Tính diện tích hình vuông EFGH.
\(Ta\) \(có\) \(S_{ABCD}=6.6=36\left(cm^2\right)\)
\(S_{EFGH}=\dfrac{1}{2}S_{ABCD}=\dfrac{1}{2}.36=18\left(cm^2\right)\)
Đúng 1
Bình luận (0)
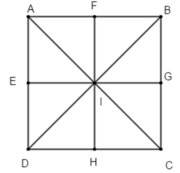
Cho hình vuông ABCD tâm I. gọi E, F, G, H lần lượt là trung điểm của các cạnh DA, AB, BC, CD. Phép đối xứng trục AC biến:
A. ∆IED thành ∆IGC
B. ∆IFB thành ∆IGB
C. ∆IBG thành ∆IDH
D. ∆IGC thành ∆IFA
Tìm ảnh của từng điểm qua phép đối xứng trục AC: điểm I biến thành I; B thành D; G thành H.
Chọn đáp án C
Đúng 0
Bình luận (0)
Cho hình vuông ABCD có cạnh bằng a. Trên cạnh AB lấy điểm E sao cho BE=2EA. Gọi F là trung điểm cạnh BC. Đường chéo AC lần lượt cắt DE,DF tại P,q. Cmr tam giác DQP và tam giác DEF đồng dạng
Cho hình chóp S.ABCD, đáy ABCD là hình bình hành , có tất cả các cạnh bằng a. Gọi E, F lần lượt là trung điểm của SA, SB Gọi M là một điểm thuộc cạnh BC sao cho BM = 2MC.
a, Chứng minh AB // (MEF)
b, Xác định thiết diện của hình chóp bị cắt bởi mặt phẳng (MEF) và tính diện tích thiết diện
Cho hình vuông ABCD có cạnh bằng a. Gọi E,F,G,H lần lượt là trung điểm của cách cạnh AB,BC,CD,DA.M là giao điểm của CE và DF.
a)CM EFGH là hình vuông
b)EC vuông góc vs DF
c)tính diện tích của tam giác MDC theo a (ko dùng đồng dạng)
Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật và AB 2a, BC a. Các cạnh bên của hình chóp bằng nhau và bằng a
2
. Gọi E và F lần lượt là trung điểm của AB và CD; K là điểm bất kỳ trên BC. Khoảng cách giữa hai đường thẳng EF và SK là: A.
a
3
3
B.
a...
Đọc tiếp
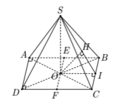
Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật và AB =2a, BC =a. Các cạnh bên của hình chóp bằng nhau và bằng a 2 . Gọi E và F lần lượt là trung điểm của AB và CD; K là điểm bất kỳ trên BC. Khoảng cách giữa hai đường thẳng EF và SK là:
A. a 3 3
B. a 6 3
C. a 15 5
D. a 21 7
Đáp án D
I là trung điểm cạnh đáy BC. Do SA = SB = SC = SD nên SO ⊥ (ABCD)
Từ đó ta chứng minh được
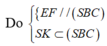
Tính được
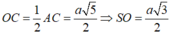
Suy ra
Đúng 0
Bình luận (0)