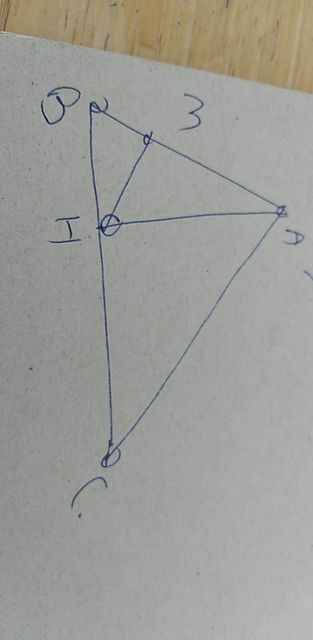
cho tam giác abc vuông tại a đường cao ah kẻ hm vuông ac, m thuộc ac. Biết ab=3 , ac=4.tính HM,MC

Những câu hỏi liên quan
Cho tam giác ABC vuông tại A (AB AC) có đường cao AH. Từ H kẻ HM ⊥ AB (M ∈ AB), kẻ HN ⊥ AC (N thuộc AC). Chứng minh tứ giác AMHN là hình chữ nhậtCho tam giác ABC vuông tại A (ABAC) có đường cao AH. Từ H kẻ HM⊥AB(M∈ AB), kẻ HN ⊥ AC(N thuộc AC)a/ AMHN là hình chữ nhậtb/ gọi I là trung điểm HC, K là điểm đối xứng với A qua I. Chứng minh AC // HKc/ chứng minh tứ giác NCKM là hình thang când/ MN cắt AH tại O, CO cắt AK tại D. Chứng minh AK3AD
Đọc tiếp
Cho tam giác ABC vuông tại A (AB < AC) có đường cao AH. Từ H kẻ HM ⊥ AB (M ∈ AB), kẻ HN ⊥ AC (N thuộc AC). Chứng minh tứ giác AMHN là hình chữ nhậtCho tam giác ABC vuông tại A (AB<AC) có đường cao AH. Từ H kẻ HM⊥AB(M∈ AB), kẻ HN ⊥ AC(N thuộc AC)
a/ AMHN là hình chữ nhật
b/ gọi I là trung điểm HC, K là điểm đối xứng với A qua I. Chứng minh AC // HK
c/ chứng minh tứ giác NCKM là hình thang cân
d/ MN cắt AH tại O, CO cắt AK tại D. Chứng minh AK=3AD
a/ AMHN là hình chữ nhật
b/ gọi I là trung điểm HC, K là điểm đối xứng với A qua I. Chứng minh AC // HK
c/ chứng minh tứ giác NCKM là hình thang cân
d/ MN cắt AH tại O, CO cắt AK tại D. Chứng minh AK=3AD
a: Xét tứ giác AMHN có
\(\widehat{AMH}=\widehat{ANH}=\widehat{MAN}=90^0\)
=>AMHN là hình chữ nhật
b: Xét tứ giác AHKC có
I là trung điểm chung của AK và HC
=>AHKC là hình bình hành
=>AC//KH
c: Ta có: AC//HK
AC//HM
HK,HM có điểm chung là H
Do đó: K,H,M thẳng hàng
Ta có: AMHN là hình chữ nhật
=>\(\widehat{NAH}=\widehat{NMH}\)
mà \(\widehat{NAH}=\widehat{CKH}\)(AHKC là hình bình hành)
nên \(\widehat{NMH}=\widehat{CKH}\)
Xét tứ giác MNCK có CN//MK
nên MNCK là hình thang
Hình thang MNCK có \(\widehat{CKM}=\widehat{NMK}\)
nên MNCK là hình thang cân
d: Ta có: AMHN là hình chữ nhật
=>AH cắt MN tại trung điểm của mỗi đường
=>O là trung điểm chung của AH và MN
Xét ΔCAH có
CO,AI là các đường trung tuyến
CO cắt AI tại D
Do đó: D là trọng tâm của ΔCAH
=>\(AD=\dfrac{2}{3}AI=\dfrac{2}{3}\cdot\dfrac{1}{2}\cdot AK=\dfrac{1}{3}AK\)
=>AK=3AD
Đúng 0
Bình luận (0)
cho tam giác ABC vuông tại A có AB=9cm,AC=12cm,đường cao AH a/ chứng minh tam giác ABC đồng dạng với tam giác HBA . Tính BC,AH. b/ kẻ HM vuông góc với AB tại M. chứng minh: HM^2=MA*MB c/ MC cắt AH tại I , đường thẳng qua I và song song với AC cắt AB,BC lần lượt tại E,F . CM: IF=IE
MỌI NGƯỜI GIÚP MÌNH VỚI Ạ!!!
a: Xét ΔABC vuông tại A và ΔHBA vuông tại H có
góc B chung
=>ΔABC đồng dạng với ΔHBA
\(BC=\sqrt{9^2+12^2}=15\left(cm\right)\)
AH=9*12/15=7,2cm
b: ΔHAB vuông tại H có HM vuông góc AB
nên MH^2=MA*MB
Đúng 0
Bình luận (0)
cho tam giác ABC vuông tại A, đường cao AH. a) Chứng minh tam giác HBA đồng dạng với tam giác ABC. b) Cho AB=15cm, AC=20cm. Tính BC, AH. c) Từ H kẻ HM vuông góc với AB, HN vuông góc với AC (M thuộc AB, N thuộc AC). Chứng minh: AB.AM=AC.AN
a: Xet ΔHBA vuông tại H và ΔABC vuông tại A có
góc B chung
=>ΔHBA đồng dạng với ΔABC
b: \(BC=\sqrt{15^2+20^2}=25\left(cm\right)\)
AH=15*20/25=12(cm)
c: ΔAHB vuông tại H có HM vuông góc AB
nên AM*AB=AH^2
ΔAHC vuông tại H có HN vuông góc AC
nên AN*AC=AH^2=AM*AB
Đúng 0
Bình luận (0)
cho tam giác ABC vuông tại A, đường cao AH. a) Chứng minh tam giác HBA đồng dạng với tam giác ABC. b) Cho AB=15cm, AC=20cm. Tính BC, AH. c) Từ H kẻ HM vuông góc với AB, HN vuông góc với AC (M thuộc AB, N thuộc AC). Chứng minh: AB.AM=AC.AN
Cho tam giác ABC vuông tại A, đường cao AH (H thuộc BC).
a, Biết AB=12cm, BC=20cm. Tính AC, AM, góc ABC.
b, Kẻ HM vuông góc AB tại M, HN vuông góc AC tại N. CM AN.AC=AC^2 - HC^2.
c, CM AH=MN, AM.MB+AN.NC=AH^2.
d, CM tan^3C=BM/CN.
b: \(AN\cdot AC=AH^2\)
\(AC^2-HC^2=AH^2\)
Do đó: \(AN\cdot AC=AC^2-HC^2\)
Đúng 0
Bình luận (3)
Cho tam giác ABC vuông tại A có AB < AC, đường cao AH. Từ H kẻ HM vuông góc với AB ( M thuộc AB ). Kẻ HN vuông góc AC ( N thuộc AC ). Gọi E là trung điểm AC, Kẻ AI vuông góc với BE tại I. Cm góc EIC= góc BIH
Cho tam giác ABC vuông A đường cao AH Kẻ HM vuông Ab(M thuộc AB) và HN vuông AC(N thuộc AC) chứng minh Tam giác AMN và ACB đồng dạng
ΔABH vuông tại H có HM vuông góc AB
nên AM*AB=AH^2
ΔACH vuông tại H có HN vuông góc AC
nên AN*AC=AH^2
=>AM*AB=AN*AC
=>AM/AC=AN/AB
=>ΔAMN đồng dạng với ΔACB
Đúng 0
Bình luận (0)
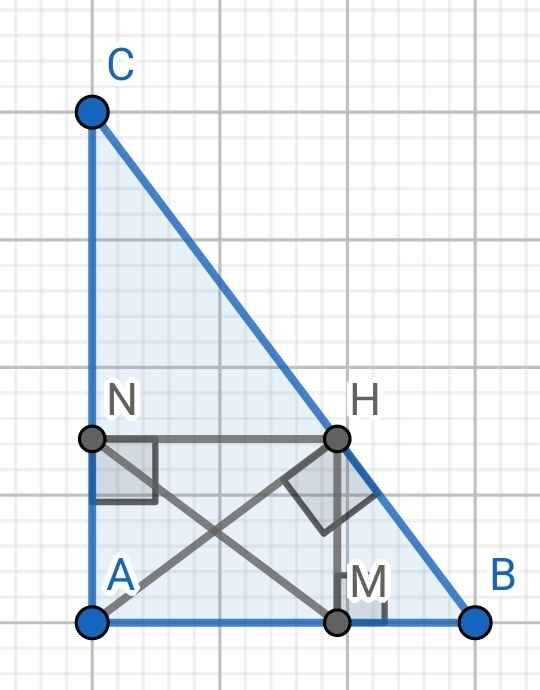
Xét hai tam giác vuông: ∆AHB và ∆AMH có:
∠A chung
⇒ ∆AHB ∽ ∆AMH (g-g)
⇒ AH/AM = AB/AH
⇒ AH² = AB.AM (1)
Xét hai tam giác vuông: ∆AHC và ∆ANH có:
∠A chung
⇒ ∆AHC ∽ ∆ANH (g-g)
⇒ AH/AN = AC/AH
⇒ AH² = AC.AN (2)
Từ (1) và (2) ⇒ AB.AM = AN.AC
⇒ AM/AC = AN/AB
Xét ∆AMN và ∆ACB có:
∠MAN = ∠ACB = 90⁰
AM/AC = AN/AB (cmt)
⇒ ∆AMN ∽ ∠∆ACB (c-g-c)
Đúng 0
Bình luận (0)
cho tam giác abc có 3 góc nhọn ( ab<ac), đường cao AH. Từ H kẻ HM vuông góc với AB tại M ( M thuộc AB)
Cho tam giác ABC vuông tại A, đường cao AH (H thuộc BC).
a, Biết AB=12cm, BC=20cm. Tính AC, AM, góc ABC.
b, Kẻ HM vuông góc AB tại M, HN vuông góc AC tại N. CM AN.AC=AC^2 - HC^2.
c, CM AH=MN, AM.MB+AN.NC=AH^2.
d, CM tan^3C=BM/CN.
mk cần phần d ak, cảm ơn trước!