câu a) mình nghĩ chứng minh ABD cân chứ ạ, sao lại ABC

Gọi H là trung điểm của AC. \(\Delta\)DAC cân tại D.

Do đó DH\(\perp\)AC và AH = \(\frac{1}{2}\)AC (1)

Vẽ AK \(\perp\)BC. Vì \(\Delta\)AKC vuông tại K và ^BCA = 30⁰

nên AK = \(\frac{1}{2}\)AC (2)

Từ (1) và (2) suy ra AK = AH

Xét \(\Delta\)AKB và \(\Delta\)AHD có:

    ^AKB = ^AHD (=90⁰)

    AK = AH(gt)

    ^BAK = ^DAH (=50⁰)

Do đó  \(\Delta\)AKB = \(\Delta\)AHD (g.c.g)

=> AB = AD

Vậy \(\Delta\)ABD cân tại A(đpcm)

Cho hình trên

Ta có

CAz là góc ngoài của A nên

CAz=B+C=50*+50*=100* (theo định lý góc ngoài của một tam giác)

Am là phân giác của CAz nên

A1=A2=\(x = {-b \pm \sqrt{b^2-4ac} \over 2a}\) 1/2 100*= 50*

=>A2=C (=50*)

Mà A2 và C là cặp góc so le trong nên

=> BC//Am (đpcm)

CHÚC BẠN HỌC TỐT

\(\widehat{B}+\widehat{C}=140^0\)

\(\Leftrightarrow4\cdot\widehat{C}=140^0\)

\(\Leftrightarrow\widehat{C}=35^0\)

hay \(\widehat{B}=105^0\)

Vậy:  ΔABC tù

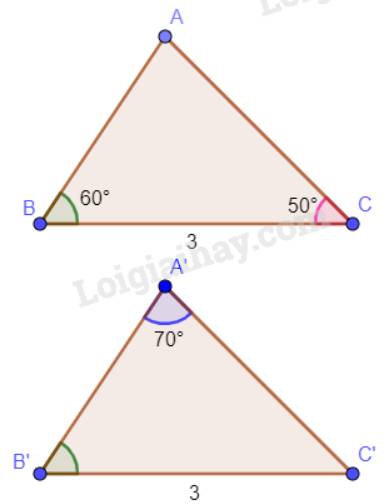
Tổng ba góc trong một tam giác bằng 180°. Vậy trong tam giác A’B’C’ có \(\widehat {C'} = 180^\circ  - 70^\circ  - 60^\circ  = 50^\circ \).

Xét hai tam giác ABC và A’B’C’ có:

     \(\widehat B = \widehat {B'} = 60^\circ ;\)

     BC = B’C’ ( = 3 cm)

     \(\widehat C = \widehat {C'} = 50^\circ \)

Vậy \(\Delta ABC = \Delta A'B'C'\)(g.c.g) 

a)

 

=> Ta có : \(\widehat{A}+\widehat{B}+\widehat{C}\) = 180^o

100^o + \(\widehat{B}+\widehat{C}\) = 180^o

\(\widehat{B}+\widehat{C}\) = 180^o - 100^o

\(\widehat{B}+\widehat{C}\) = 80^o

Góc B = (80^o+50^o):2 = 65^o

=> \(\widehat{C}\) = 65^o - 50^o = 15^o

Vậy \(\widehat{B}\) = 65^o ; \(\widehat{C}\) = 15^o

b)

 

Ta có : \(\widehat{3A}+\widehat{B}+\widehat{2C}\) = 180^o

\(\widehat{3A}+\widehat{2C}\) = 180^o - 80^o

\(\widehat{3A}+\widehat{2C}\) = 100^o

=> \(\widehat{A}\) = 100^o:(3+2).3 = 60^o

\(\widehat{C}\) = 100^o - 60^o = 40^o

Vậy \(\widehat{A}\) = 60^o ; \(\widehat{C}\) = 40^o

a) Do \(\widehat{A}=100^0>90^0\) nên là góc tù, do đó, \(\widehat{A}\) là góc lớn nhất trong tam giác ABC.

\( \Rightarrow \) BC là cạnh lớn nhất của tam giác ABC (do BC đối diện với góc A trong tam giác ABC)

b) 

Theo định lí tổng 3 góc trong tam giác ABC, ta có:

\( \Rightarrow \widehat A + \widehat B + \widehat C = {180^o}\)

\( \Rightarrow \widehat C = {180^o} - {100^o} - {40^o} = {40^o}\)

 \( \Rightarrow\widehat C = \widehat B = {40^o}\)

\( \Rightarrow \) ABC là tam giác cân tại A.

a) Theo đề bài ta có AB = 4cm, BC = 7cm, AC = 6cm

Có góc đối diện với cạnh AB là góc C, góc A đối diện với cạnh BC, góc B đối diện với cạnh AC

Theo định lí về góc đối diện với cạnh lớn hơn thì lớn hơn ta có :

\( \Rightarrow \widehat A > \widehat B > \widehat C\)

b)

Vì \(\widehat{A}=\widehat{C}\) nên tam giác ABC cân tại B

\( \Rightarrow BA = BC\)

Áp dụng định lí tổng 3 góc trong tam giác ABC, có:

\( \Rightarrow \widehat B = {180^o} - {100^0} = {80^o}\)

\( \Rightarrow \widehat B > \widehat A=\widehat C\)

\( \Rightarrow AC\) là cạnh lớn nhất tam giác ABC (Quan hệ giữa góc và cạnh đối diện trong tam giác)