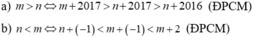(a:1+a*1):(2017*n+m)

Những câu hỏi liên quan
Cho a+b+c=2017 thỏa mãn \(\dfrac{1}{a}+\dfrac{1}{b}+\dfrac{1}{c}\) Tính M = \(a^{2017}+b^{2017}+c^{2017}\)
cho các số dương thỏa mãn (b+c)/a^2+(a+c)/b^2+(a+b)/c^2=2(1/a+1/b+1/c). tính gtbt: P= (a-b)^2017 + (b-c)^2017 + (c-a)^2017
Cho các số a,b,c thoã mãn : 1/ a+b+c = 1/a + 1/b + 1/c
Tính giá trị biểu thức S=a2017+b2017+c2017/ ( a+b+c )2017
cho 3 số a,b,c thỏa mãn ; a+b+c=2017 và 1/a+1/b+1/c=1/2017
cmr có ít nhất 1 trong 3 số = 2017
giải gấp hộ e với. Thanks
bài 1: cho 3 số a,b,c thỏa mãn:
1/a + 1/b + 1/c 1/a+b+c
CMR: 1/a2017 + 1/b2017 + 1/c2017 1/a2017+b2017+c2017
bài 2
cho a,b,c ∈ Z thỏa mãn: a3+b3 2c3
CMR: a+b+c ⋮ 3
@Akai Haruma @Mysterious Person giải theo cách lớp 8 ạ
Đọc tiếp
bài 1: cho 3 số a,b,c thỏa mãn:
1/a + 1/b + 1/c = 1/a+b+c
CMR: 1/a2017 + 1/b2017 + 1/c2017 = 1/a2017+b2017+c2017
bài 2
cho a,b,c ∈ Z thỏa mãn: a3+b3 = 2c3
CMR: a+b+c ⋮ 3
@Akai Haruma @Mysterious Person giải theo cách lớp 8 ạ
Bài 1:
Ta có:
\(\frac{1}{a}+\frac{1}{b}+\frac{1}{c}=\frac{1}{a+b+c}\)
\(\Leftrightarrow \left(\frac{1}{a}+\frac{1}{b}\right)+\frac{1}{c}-\frac{1}{a+b+c}=0\)
\(\Leftrightarrow \frac{a+b}{ab}+\frac{a+b+c-c}{c(a+b+c)}=0\)
\(\Leftrightarrow (a+b)\left(\frac{1}{ab}+\frac{1}{c(a+b+c)}\right)=0\)
\(\Leftrightarrow (a+b).\frac{c(a+b+c)+ab}{abc(a+b+c)}=0\Leftrightarrow (a+b).\frac{c(c+a)+b(a+c)}{abc(a+b+c)}=0\)
\(\Leftrightarrow \frac{(a+b)(b+c)(c+a)}{abc(a+b+c)}=0\Rightarrow (a+b)(b+c)(c+a)=0\)
\(\Rightarrow \left[\begin{matrix} a+b=0\\ b+c=0\\ c+a=0\end{matrix}\right.\)
Ta xét TH $a+b=0\Rightarrow a=-b$, các TH khác làm tương tự:
Khi đó: \(\frac{1}{a^{2017}+b^{2017}+c^{2017}}=\frac{1}{(-b)^{2017}+b^{2017}+c^{2017}}=\frac{1}{c^{2017}}\)
Và: \(\frac{1}{a^{2017}}+\frac{1}{b^{2017}}+\frac{1}{c^{2017}}=\frac{1}{(-b)^{2017}}+\frac{1}{b^{2017}}+\frac{1}{c^{2017}}=\frac{1}{c^{2017}}\)
Do đó: \(\frac{1}{a^{2017}}+\frac{1}{b^{2017}}+\frac{1}{c^{2017}}=\frac{1}{a^{2017}+b^{2017}+c^{2017}}\)
Ta có đpcm.
Đúng 0
Bình luận (0)
Bài 2:
Ta có:
Áp dụng công thức quen thuộc (suy ra trực tiếp từ hằng đẳng thức đáng nhớ): \(x^3+y^3=(x+y)^3-3xy(x+y)\) ta có:
\(a^3+b^3=2c^3\)
\(\Leftrightarrow a^3+b^3+c^3=3c^3\)
\(\Leftrightarrow (a+b)^3-3ab(a+b)+c^3=3c^3\)
\(\Leftrightarrow (a+b)^3+c^3-3ab(a+b)=3c^3\)
\(\Leftrightarrow (a+b+c)^3-3(a+b).c(a+b+c)-3ab(a+b)=3c^3\)
\(\Leftrightarrow (a+b+c)^3=3c^3+3ab(a+b)+3(a+b)c(a+b+c)\vdots 3\)
Mà $3\in\mathbb{P}$ nên \(\Rightarrow a+b+c\vdots 3\)
Ta có đpcm.
Đúng 0
Bình luận (0)
Cho m > n, chứng minh:
a) m + 2017 > n + 2016 b) n - 1 < m + 2
Cho các số nguyên a1, a2, a3 .................a2017thỏa mãn
a1 + a2 + a3 .................+a2017 = 0
a1 + a2 + a3 + a4 +....................= a2015 + a2016+ a2017 +a1=1
Tính a1, a2, a2017
Cho 3 số a,b,c thỏa mãn ab + bc + ca = 2017abc và 2017(a + b + c) = 1
Tính A = a2017 + b2017 + c2017
- Nếu một trong các số a;b;c bằng 0, giả sử là a
\(\Rightarrow bc=0\Rightarrow\left\{{}\begin{matrix}b=0\\c=\frac{1}{2017}\end{matrix}\right.\)
\(\Rightarrow A=\frac{1}{2017^{2017}}\)
- Nếu a;b;c đều khác 0
\(ab+bc+ca=2017abc\Rightarrow\frac{1}{a}+\frac{1}{b}+\frac{1}{c}=2017\)
\(\Rightarrow\left\{{}\begin{matrix}\frac{1}{a}+\frac{1}{b}+\frac{1}{c}=2017\\\frac{1}{a+b+c}=2017\end{matrix}\right.\) \(\Rightarrow\frac{1}{a}+\frac{1}{b}+\frac{1}{c}=\frac{1}{a+b+c}\)
\(\Leftrightarrow\frac{a+b}{ab}+\frac{1}{c}-\frac{1}{a+b+c}=0\Leftrightarrow\frac{a+b}{ab}+\frac{a+b}{c\left(a+b+c\right)}=0\)
\(\Leftrightarrow\left(a+b\right)\left(\frac{1}{ab}+\frac{1}{c\left(a+b+c\right)}\right)=0\)
\(\Leftrightarrow\left(a+b\right)\left(\frac{ab+bc+ca+c^2}{abc\left(a+b+c\right)}\right)=0\)
\(\Leftrightarrow\left(a+b\right)\left(b+c\right)\left(c+a\right)=0\Rightarrow\left[{}\begin{matrix}a=-b;c=\frac{1}{2017}\\b=-c;a=\frac{1}{2017}\\c=-a;b=\frac{1}{2017}\end{matrix}\right.\)
\(\Rightarrow A=\frac{1}{2017^{2017}}\)
Như vậy trong mọi trường hợp ta luôn có \(A=\frac{1}{2017^{2017}}\)
Đúng 0
Bình luận (0)
Câu a: Tìm n thuộc Z để A=(2n+1/n+3)-n-5/n+3
Nhận giá trị nguyên
Câu b: Cho a+2b/b=b+2c/c=c+2a/a với a,b,c khác 0
Tính M=(1+a/b)(1+b/c)(1+c/a)
Câu c: a,b,c thuộc Z+ thỏa mãn :a/a+2b =b/b+2c=c/c+2a
CMR :a+b+c chia hết cho 3
Câu d: Cho xt=yz
CMR : (x-y/z-t)^2017=x^2017+y^2017/z^2017+t^2017
Ai giải dùm mình với T^T