Cho x+ y = m và x.y = n.Tính giá trị các biểu thức sau theo m,n.
c) x7 + y7
Cho x + y = a và x.y = b . Tính giá trị của biểu thức theo a và b
M= x2 + y2
M=x2+y2
=(x2+2xy+y2)-2xy
=(x+y)2-2xy
=a2-2b
Cho x+y=a; x.y=b. Tính giá trị biểu thức sau theo a và b:
x4+y4
\(x^4+y^4=\left(x^2+y^2\right)^2-2x^2y^2=\left[\left(x+y\right)^2-2xy\right]^2-2\left(xy\right)^2\)
\(=\left(a^2-2b\right)^2-2b^2=a^4-2.a^2.2b+4b^2-2b^2=a^4-4a^2b+2b^2\)
x7 + y7. Tính giá trị biểu thức
Tính giá trị biểu thức : M=x^3 - y^3 Biết x-y=4 và x.y=3
Ta có: \(x-y=4\Rightarrow\left(x-y\right)^2=16\)
\(\Rightarrow x^2-2xy+y^2=16\Rightarrow x^2+y^2=16+2xy=16+2.3=22\)
\(M=x^3-y^3=\left(x-y\right)\left(x^2+xy+y^2\right)=4.\left(22+3\right)=100\)
Cho a+b+c=m Và (1/a+b)+(1/b+c)+(1/c+a)=n.Tính theo m,n giá trị biểu thức S: S=(a/b+c)+(b/c+a)+(c/a=b)
cho x+y=2, x.y=-1. Tìm P= x7 + y7
\(x^2+y^2=\left(x+y\right)^2-2xy=6\)
\(x^3+y^3=\left(x+y\right)^3-3xy.\left(x+y\right)=14\)
\(x^4+y^4=\left(x^2+y^2\right)^2-2\left(xy\right)^2=34\)
\(\Rightarrow x^7+y^7=\left(x^3+y^3\right)\left(x^4+y^4\right)-\left(xy\right)^3\left(x+y\right)=478\)
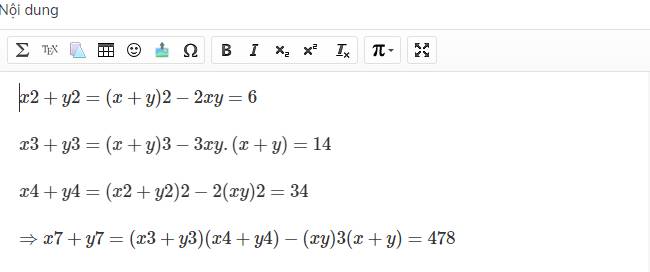 \(x2+y2=(x+y)2−2xy=6\)
\(x2+y2=(x+y)2−2xy=6\)
\(x3+y3=(x+y)3−3xy.(x+y)=14\)
\(x4+y4=(x2+y2)2−2(xy)2=34\)
\(⇒x7+y7=(x3+y3)(x4+y4)−(xy)3(x+y)=478\)
1 . Cho x+y=a và x.y=b . Tính giá trị biểu thức sau theo a và b :
a) x2 + y2
b) x3 + y3
c) x4 + y4
d) x5 + y5
2 . Cho x+y=1 .Tính giá trị biểu thức x3 + y3 + 3xy và x-y=1 .Tính giá trị biểu thức x3 - y3 - 3xy
3 . Cho a+b=1 . Tính giá trị biểu thức : M = a3 + b3 + 3ab .( 12 + b2 ) + 6.a2 .b2 . ( a+b)
cho x+y=3 x.y=5 tính giá trị các biểu thức sau a) x^2+y^2. b) x^3+y^3 c) x^4+y^4
Đề sai rồi, không thể tồn tại x; y sao cho \(\left\{{}\begin{matrix}x+y=3\\xy=5\end{matrix}\right.\) được
Vì \(\left(x+y\right)^2\ge4xy;\forall x;y\) nên \(3^2>4.5\) là vô lý
a: \(x^2+y^2=\left(x+y\right)^2-2xy=3^2-2\cdot5=-1\)
b: \(x^3+y^3=\left(x+y\right)^3-3xy\left(x+y\right)=3^3-3\cdot3\cdot5=-18\)
Trong các biểu thức dưới đây, giá trị của biểu thức nào là lớn nhất?
M = [(-3) + 4] + 2;
N = (-3) + (4 + 2);
P = [(-3) + 2] + 4.
A. M.
B. N.
C. P.
D. Không có giá trị biểu thức nào lớn nhất.