Với a, b là hai số bất kì , hãy tính [ a+(-b)3 ] theo hai cách.
Với a và b là hai số bất kì, thức hiện phép tính (a + b)(a + b).
(a + b)(a + b) = a(a + b) + b(a + b)
= a2 + ab + ba + b2
= a2 + 2ab + b2
Cho a và b là hai số tự nhiên bất kì hãy chứng tỏ 12345a+6789bchia hết cho 3
Cho a và b là hai số tự nhiên bất kì hãy chứng tỏ(12345a+6789b)chia hết cho 3
ta có
12345a chia hết cho 3 vì 12345 chia hết cho 3
6789a chia hết cho 3 vì 6789 chia hết cho 3
=> 12345a+6789b chia hết cho 3 ( đpcm)
Với a,b là hai số tự nhiên bất kì , số ab. ( a + b ) luôn là
Với a;b là 2 số tự nhiên bất kì , số ab.(a+b) luôn là hợp số hoặc số chẵn.
Cho A và B là hai tập hợp bất kì. Trong mỗi cặp tập hợp sau đây, tập hợp nào là tập con của tập hợp còn lại? Hãy giải thích bằng cách sử dụng biểu đồ Ven.
a) A và \(A \cup B\)
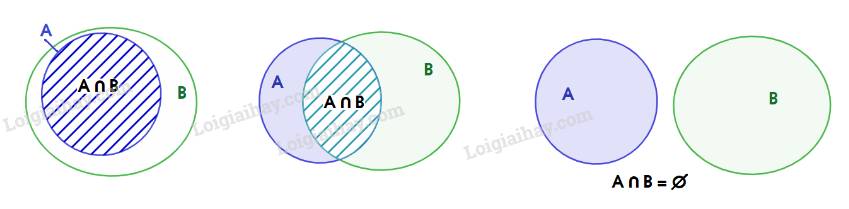
b) A và \(A \cap B\)
Tham khảo:
a) \(A \subset A \cup B\) vì
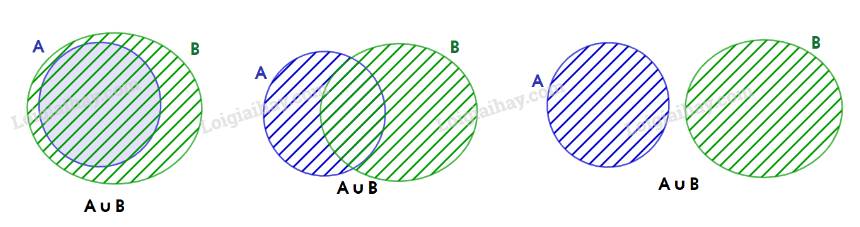
b) \(A \cap B \subset A\) vì
Cho hai đường thẳng song song a và b (h.93).
Gọi A và B là hai điểm bất kì thuộc đường thẳng a, AH và BK là các đường vuông góc kẻ từ A và B đến đường thẳng b. Gọi độ dài AH là h. Tính độ dài BK theo h.
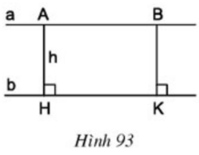
AH // BK (cùng ⊥ b) và AB // HK ⇒ tứ giác ABKH là hình bình hành
⇒ AH = BK = h
Hãy nối mỗi ô của cột A với mỗi ô của cột B để được các phát biểu đúng :
| Cột A | Cột B |
| 1. Nếu hai đại lượng tỉ lệ thuận với nhau thì tỉ số giữa hai giá trị tương ứng của chúng | a) Bằng tỉ số giữa hai giá trị tương ứng của đại lượng kia. |
| 2. Nếu hai đại lượng tỉ lệ thuận với nhau thì tỉ số giữa hai đại lượng bất kì của đại lượng này | b) Bằng nghịch đảo của tỉ số hai giá trị tương ứng của đại lượng kia |
| 3. Nếu hai đại lượng tỉ lệ nghịch với nhau thì tích hai giá trị tương ứng | c) luôn không đổi |
| 4. Nếu hai đại lượng tỉ lệ nghịch với nhau thì tỉ số hai giá trị bất kì của đại lượng này |
Chứng minh rằng a5b - ab chia hết cho 30 với a,b là hai số nguyên bất kì.
Với a,b là hai số thực dương bất kì. Số điểm cực trị của hàm số y = x 3 + a x 2 - b x + 1 là
A. 2.
B. 0.
C. 3.
D. 1.
Với a,b là hai số thực dương bất kì. Số điểm cực trị của hàm số y = x 3 + a x 2 - b x + 1 là
A. 2.
B. 0.
C. 3.
D. 1.