Gọi \(A=\sum\dfrac{x^3}{\sqrt{y^2+3}}\)

Theo Holder: \(A.A.\left(\left(y^2+3\right)+\left(z^2+3\right)+\left(x^2+3\right)\right)\ge\left(x^3+y^3+z^3\right)^3\)

\(\Rightarrow A^2\ge\dfrac{\left(x^3+y^3+z^3\right)^3}{x^2+y^2+z^2+9}\ge\dfrac{\left(x^3+y^3+z^3\right)^3}{x^2+y^2+z^2+3\left(xy+yz+zx\right)}=\dfrac{\left(x^3+y^3+z^3\right)^3}{\left(x+y+z\right)^2+xy+yz+zx}\ge\dfrac{\left(x^3+y^3+z^3\right)^3}{\left(x+y+z\right)^2+\dfrac{\left(x+y+z\right)^2}{3}}\)

Ta có đánh giá sau: \(x^3+y^3+z^3\ge\dfrac{\left(x^2+y^2+z^2\right)^2}{x+y+z}\ge\dfrac{\left(x+y+z\right)^3}{9}\)

\(\Rightarrow A^2\ge\dfrac{\dfrac{\left(x+y+z\right)^3}{9}}{\left(x+y+z\right)^2+\dfrac{\left(x+y+z\right)^2}{3}}=\dfrac{x+y+z}{12}\ge\dfrac{\sqrt{3\left(xy+yz+zx\right)}}{12}\ge\dfrac{1}{4}\)

\(\Rightarrow A\ge\dfrac{1}{2}\)

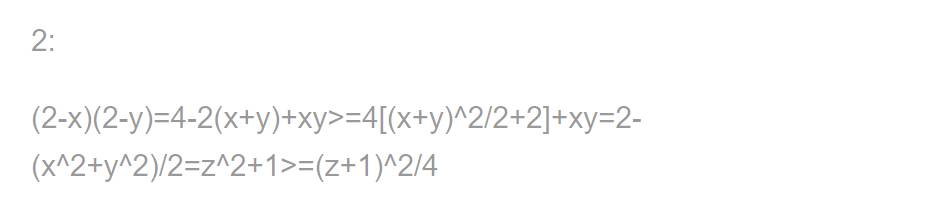
Tương tự, ta được:

\(\left(2-y\right)\left(2-z\right)>=\dfrac{\left(x+1\right)^2}{4}\)

và \(\left(2-z\right)\left(2-x\right)>=\left(\dfrac{y+1}{2}\right)^2\)

=>8(2-x)(2-y)(2-z)>=(x+1)(y+1)(z+1)

(x+yz)(y+zx)<=(x+y+yz+xz)^2/4=(x+y)^2*(z+1)^2/4<=(x^2+y^2)(z+1)^2/4

Tương tự, ta cũng co:

\(\left(y+xz\right)\left(z+y\right)< =\dfrac{\left(y^2+z^2\right)\left(x+1\right)^2}{2}\)

và \(\left(z+xy\right)\left(x+yz\right)< =\dfrac{\left(z^2+x^2\right)\left(y+1\right)^2}{2}\)

Do đó, ta được:

\(\left(x+yz\right)\left(y+zx\right)\left(z+xy\right)< =\left(x+1\right)\left(y+1\right)\left(z+1\right)\)

=>ĐPCM

Lời giải:

Từ \(xy+yz+xz=xyz\Rightarrow \frac{1}{x}+\frac{1}{y}+\frac{1}{z}=1\)

Đặt \((a,b,c)=\left(\frac{1}{x}; \frac{1}{y}; \frac{1}{z}\right)\Rightarrow a+b+c=1\)

BĐT cần chứng minh trở thành:

\(P=\frac{c^3}{(a+1)(b+1)}+\frac{a^3}{(b+1)(c+1)}+\frac{b^3}{(c+1)(a+1)}\geq \frac{1}{16}(*)\)

Thật vậy, áp dụng BĐT Cauchy ta có:

\(\frac{c^3}{(a+1)(b+1)}+\frac{a+1}{64}+\frac{b+1}{64}\geq 3\sqrt[3]{\frac{c^3}{64^2}}=\frac{3c}{16}\)

\(\frac{a^3}{(b+1)(c+1)}+\frac{b+1}{64}+\frac{c+1}{64}\geq 3\sqrt[3]{\frac{a^3}{64^2}}=\frac{3a}{16}\)

\(\frac{b^3}{(c+1)(a+1)}+\frac{c+1}{64}+\frac{a+1}{64}\geq 3\sqrt[3]{\frac{b^3}{64^2}}=\frac{3b}{16}\)

Cộng theo vế các BĐT trên và rút gọn :

\(\Rightarrow P+\frac{a+b+c+3}{32}\geq \frac{3(a+b+c)}{16}\)

\(\Leftrightarrow P+\frac{4}{32}\geq \frac{3}{16}\Leftrightarrow P\geq \frac{1}{16}\)

Vậy \((*)\) được chứng minh. Bài toán hoàn tất.

Dấu bằng xảy ra khi \(a=b=c=\frac{1}{3}\Leftrightarrow x=y=z=3\)

Từ \(xyzt=1\) ta có: \(\dfrac{1}{x^3\left(yz+zt+ty\right)}=\dfrac{xyzt}{x^3\left(yz+zt+ty\right)}=\dfrac{yzt}{x^2\left(yz+zt+ty\right)}\)

Đánh giá tương tự ta có:

\(pt\Leftrightarrow\dfrac{yzt}{x^2\left(yz+zt+ty\right)}+\dfrac{xzt}{y^2\left(xz+zt+tx\right)}+\dfrac{xyt}{z^2\left(xy+yt+tx\right)}+\dfrac{xyz}{t^2\left(xy+yz+zx\right)}\ge3\left(yzt+xzt+xyt+xyz\right)=3yzt+3xzt+3xyt+3xyz\)

Ta sẽ chứng minh:

\(\dfrac{yzt}{x^2\left(yz+zt+ty\right)}\ge3yzt\). Cộng theo vế rồi suy ra đpcm

T gần đi học r,có gì tối về giải full cho

Áp dụng cauchy-schwarz:

\(VT=\sum\dfrac{\dfrac{1}{x^2}}{\dfrac{1}{y}+\dfrac{1}{z}+\dfrac{1}{t}}\ge\dfrac{\left(\dfrac{1}{x}+\dfrac{1}{y}+\dfrac{1}{z}+\dfrac{1}{t}\right)^2}{3\left(\dfrac{1}{x}+\dfrac{1}{y}+\dfrac{1}{z}+\dfrac{1}{t}\right)}=VF\)

@Neet

\(VT=\dfrac{1}{x^3\left(yz+zt+ty\right)}+\dfrac{1}{y^3\left(xz+zt+tx\right)}+\dfrac{1}{z^3\left(xy+yt+tx\right)}+\dfrac{1}{t^3\left(xy+yz+xz\right)}\)

\(=\dfrac{\dfrac{1}{x^2}}{xyz+xzt+xyt}+\dfrac{\dfrac{1}{y^2}}{xyz+yzt+txy}+\dfrac{\dfrac{1}{z^2}}{xyz+yzt+ztx}+\dfrac{\dfrac{1}{t^2}}{xyt+yzt+txz}\)

\(=\dfrac{\dfrac{1}{x^2}}{\dfrac{xyz}{xyzt}+\dfrac{xzt}{xyzt}+\dfrac{xyt}{xyzt}}+\dfrac{\dfrac{1}{y^2}}{\dfrac{xyz}{xyzt}+\dfrac{yzt}{xyzt}+\dfrac{txy}{xyzt}}+\dfrac{\dfrac{1}{z^2}}{\dfrac{xyz}{xyzt}+\dfrac{yzt}{xyzt}+\dfrac{ztx}{xyzt}}+\dfrac{\dfrac{1}{t^2}}{\dfrac{xyt}{xyzt}+\dfrac{yzt}{xyzt}+\dfrac{txz}{xyzt}}\)

\(=\dfrac{\dfrac{1}{x^2}}{\dfrac{1}{t}+\dfrac{1}{y}+\dfrac{1}{z}}+\dfrac{\dfrac{1}{y^2}}{\dfrac{1}{t}+\dfrac{1}{x}+\dfrac{1}{z}}+\dfrac{\dfrac{1}{z^2}}{\dfrac{1}{t}+\dfrac{1}{x}+\dfrac{1}{y}}+\dfrac{\dfrac{1}{t^2}}{\dfrac{1}{z}+\dfrac{1}{x}+\dfrac{1}{y}}\)

\(\ge\dfrac{\left(\dfrac{1}{x}+\dfrac{1}{y}+\dfrac{1}{z}+\dfrac{1}{t}\right)^2}{3\left(\dfrac{1}{x}+\dfrac{1}{y}+\dfrac{1}{z}+\dfrac{1}{t}\right)}=\dfrac{1}{3}\left(\dfrac{1}{x}+\dfrac{1}{y}+\dfrac{1}{z}+\dfrac{1}{t}\right)=VP\)

Lời giải:

Ta có: \(xy+yz+xz=3xyz\Rightarrow \frac{1}{x}+\frac{1}{y}+\frac{1}{z}=3\)

Mà theo BĐT Cauchy-Schwarz: \(\frac{1}{x}+\frac{1}{y}+\frac{1}{z}\geq \frac{9}{x+y+z}\)

Do đó: \(3\geq \frac{9}{x+y+z}\Rightarrow x+y+z\geq 3\)

-------

Ta có: \(\text{VT}=x-\frac{xz}{x^2+z}+y-\frac{xy}{y^2+x}+z-\frac{yz}{z^2+y}\)

\(=(x+y+z)-\left(\frac{xy}{y^2+x}+\frac{yz}{z^2+y}+\frac{xz}{x^2+z}\right)\)

\(\geq x+y+z-\frac{1}{2}\left(\frac{xy}{\sqrt{xy^2}}+\frac{yz}{\sqrt{z^2y}}+\frac{xz}{\sqrt{x^2z}}\right)\) (AM-GM)

\(=x+y+z-\frac{1}{2}(\sqrt{x}+\sqrt{y}+\sqrt{z})\)

Tiếp tục AM-GM: \(\sqrt{x}+\sqrt{y}+\sqrt{z}\leq \frac{x+1}{2}+\frac{y+1}{2}+\frac{z+1}{2}=\frac{x+y+z+3}{2}\)

Suy ra:

\(\text{VT}\geq x+y+z-\frac{1}{2}.\frac{x+y+z+3}{2}=\frac{3}{4}(x+y+z)-\frac{3}{4}\)

\(\geq \frac{9}{4}-\frac{3}{4}=\frac{3}{2}=\frac{1}{2}\left(\frac{1}{x}+\frac{1}{y}+\frac{1}{z}\right)\)

Ta có đpcm

Dấu bằng xảy ra khi $x=y=z=1$

Sửa lại đề: cho x, y, z dương thỏa mãn \(\dfrac{1}{xy}+\dfrac{1}{xz}+\dfrac{1}{yz}=1\)

Chứng minh \(A=\dfrac{x}{\sqrt{yz\left(1+x^2\right)}}+\dfrac{y}{\sqrt{xz\left(1+y^2\right)}}+\dfrac{z}{\sqrt{xy\left(1+z^2\right)}}\le\dfrac{3}{2}\)

Giải:

Đặt \(a=\dfrac{1}{x};b=\dfrac{1}{y};c=\dfrac{1}{z}\Rightarrow ab+bc+ac=1\)

\(\Rightarrow A=\dfrac{\dfrac{1}{a}}{\sqrt{\dfrac{1}{bc}\left(1+\dfrac{1}{a^2}\right)}}+\dfrac{\dfrac{1}{b}}{\sqrt{\dfrac{1}{ac}\left(1+\dfrac{1}{b^2}\right)}}+\dfrac{\dfrac{1}{a}}{\sqrt{\dfrac{1}{ab}\left(1+\dfrac{1}{c^2}\right)}}\)

\(\Rightarrow A=\sqrt{\dfrac{bc}{a^2+1}}+\sqrt{\dfrac{ac}{b^2+1}}+\sqrt{\dfrac{ab}{c^2+1}}\)

\(\Rightarrow A=\sqrt{\dfrac{bc}{a^2+ab+bc+ac}}+\sqrt{\dfrac{ac}{b^2+ab+bc+ac}}+\sqrt{\dfrac{ab}{c^2+ab+bc+ac}}\)

\(\Rightarrow A=\sqrt{\dfrac{bc}{\left(a+b\right)\left(a+c\right)}}+\sqrt{\dfrac{ac}{\left(a+b\right)\left(b+c\right)}}+\sqrt{\dfrac{ab}{\left(a+c\right)\left(b+c\right)}}\)

\(\Rightarrow A\le\dfrac{1}{2}\left(\dfrac{b}{a+b}+\dfrac{c}{a+c}+\dfrac{a}{a+b}+\dfrac{c}{b+c}+\dfrac{a}{a+c}+\dfrac{b}{b+c}\right)\)

\(\Rightarrow A\le\dfrac{1}{2}\left(\dfrac{a+b}{a+b}+\dfrac{b+c}{b+c}+\dfrac{a+c}{a+c}\right)=\dfrac{3}{2}\) (đpcm)

Dấu "=" xảy ra khi \(a=b=c=\dfrac{\sqrt{3}}{3}\) hay \(x=y=z=\sqrt{3}\)

Đề bài này có rất nhiều vấn đề, đầu tiên không có điều kiện x, y, z gì cả? Dương? Â? Bằng 0? Khác 0?

Sau nữa là chiều của BĐT cũng có vấn đề nốt, mình thử với \(x=y=2;z=\dfrac{4}{3}\) thì vế trái ra \(\dfrac{2+\sqrt{30}}{5}\) mà theo casio cho biết thì số này nhỏ hơn \(\dfrac{3}{2}\) , vậy BĐT cũng sai luôn

nhầm nha: x, y, z > 0

Bạn tham khảo lời giải tại đây:

cho các số thực dưong x,y,z thỏa mãn : x2 y2 z2=3chứng minh rằng : \(\dfrac{x}{\sqrt[3]{yz}} \dfrac{y}{\sqrt[3]{zx}} \df... - Hoc24

Cách khác:

Áp dụng BĐT AM-GM và BĐT Cauchy-Schwarz:

\(\sum \frac{x}{\sqrt[3]{yz}}\geq \sum \frac{x}{\frac{y+z+1}{3}}=3\sum \frac{x}{y+z+1}=3\sum \frac{x^2}{xy+xz+x}\)

\(\geq 3. \frac{(x+y+z)^2}{2(xy+yz+xz)+(x+y+z)}\)

Ta sẽ chứng minh: \(\frac{3(x+y+z)^2}{2(xy+yz+xz)+(x+y+z)}\geq xy+yz+xz(*)\)

Đặt $x+y+z=a$ thì $xy+yz+xz=\frac{a^2-3}{2}$

Bằng BĐT AM-GM dễ thấy $\sqrt{3}< a\leq 3$

BĐT $(*)$ trở thành:

$\frac{3a^2}{a^2+a-3}\geq \frac{a^2-3}{2}$

$\Leftrightarrow a^4+a^3-12a^2-3a+9\leq 0$

$\Leftrightarrow (a-3)(a+1)(a^2+3a-3)\leq 0$

Điều này đúng với mọi $\sqrt{3}< a\leq 3$

Do đó BĐT $(*)$ đúng nên ta có đpcm.

Dấu "=" xảy ra khi $x=y=z=1$