vẽ đồ thị hàm số y=2x2+x+1
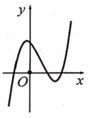
Hàm số y = ( x - 2 ) ( x 2 - 1 ) có đồ thị như hình vẽ bên.
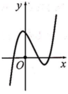
Hình nào dưới đây là đồ thị của hàm số y = x - 2 x 2 - 1
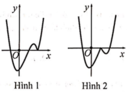
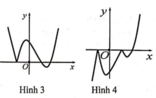
A. Hình 1
B. Hình 2
C. Hình 3
D. Hình 4
Hàm số y = ( x - 2 ) ( x 2 - 1 ) có đồ thị như hình vẽ bên. Hình nào dưới đây là đồ thị của hàm số y = x - 2 x 2 - 1 ?
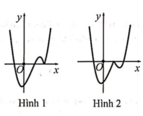
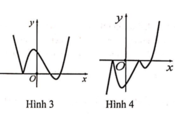
A. Hình 1
B. Hình 2
C. Hình 3
D. Hình 4
Hàm số y = ( x - 2 ) ( x 2 - 1 ) có đồ thị như hình vẽ bên.
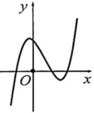
Hình nào dưới đây là đồ thị của hàm số y = x - 2 x 2 - 1

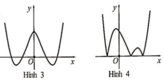
A. Hình 1
B. Hình 2
C. Hình 3
D. Hình 4
Hàm số y = x - 2 x 2 - 1 có đồ thị như hình vẽ bên.
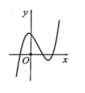
Hình nào dưới đây là đồ thị của hàm số y = x - 1 x 2 - x - 2
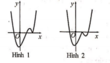
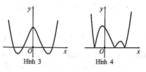
A. Hình 1
B. Hình 2
C. Hình 3
D. Hình 4
Hàm số y = x - 2 x 2 - 1 có đồ thị như hình vẽ bên. Hình nào dưới đây là đồ thị của hàm số y = x + 1 x 2 - 3 x + 2 ?
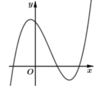
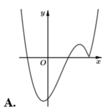
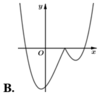
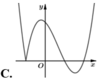
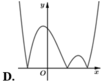
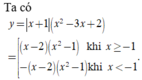
Suy ra đồ thị của hàm số
y
=
x
-
2
x
2
-
1
giống y chang phần đồ thị của hàm số ![]()
(bên phải đường thẳng x = -1). Đối chiếu các đáp án ta chọn C.
Hàm số y = x - 2 x 2 - 1 có đồ thị như hình vẽ bên. Hình nào dưới đây là đồ thị của hàm số y = x + 1 x 2 - 3 x + 2 ?
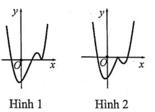
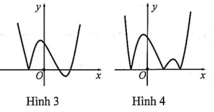
A. Hình 1.
B. Hình 2.
C. Hình 3.
D. Hình 4
Lập bảng biến thiên và vẽ đồ thị của các hàm số: y = 2x2 + x + 1
y = 2x2 + x + 1
+ Tập xác định: R
+ Đỉnh A(–1/4 ; 7/8).
+ Trục đối xứng x = –1/4.
+ Đồ thị không giao với trục hoành.
+ Giao điểm với trục tung B(0; 1).
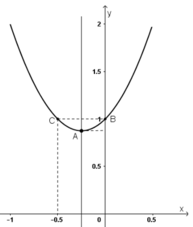
Điểm đối xứng với B(0 ; 1) qua đường thẳng x = –1/4 là C(–1/2 ; 1)
+ Bảng biến thiên:
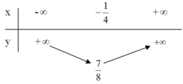
+ Đồ thị hàm số:
Hãy vẽ đồ thị của các hàm số y = 2x2, y = -2x2. Dựa vào đồ thị để trả lời các câu hỏi sau:
Đồ thị của hàm số y = ax2 có những đặc điểm gì (trường hợp a > 0 , trường hợp a < 0)
Đồ thị hàm số y = ax2 là đường cong (đặt tên là parabol) đi qua gốc tọa độ nhận trục tung Oy làm trục đối xứng.
Nếu a > 0 thì đồ thị nằm trên trục hoành, điểm O là điểm thấp nhất đồ thị (gọi là đỉnh parabol).
Nếu a < 0 thì đồ thị nằm bên dưới trục hoành, điểm O là điểm cao nhất của đồ thị.
Cho hàm số y = 2 x 2 + 2 m x + m - 1 có đồ thị là C m , m là tham số.
Khảo sát sự biến thiên và vẽ đồ thị hàm số khi m = -1
Với m = 1 ta được hàm số: y = 2 x 2 + 2 x
- TXĐ: D = R,
- Sự biến thiên:
+ Chiều biến thiên: y' = 4x + 2
y' = 0 ⇔ x = -1/2
+ Bảng biến thiên:
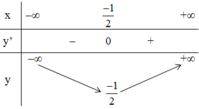
Kết luận: Hàm số nghịch biến trên (-∞; -1/2), đồng biến trên (-1/2; +∞).
Đồ thị hàm số có điểm cực tiểu là (-1/2; -1/2)
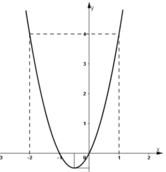
- Đồ thị:
Ta có: 2x2 + 2x = 0 ⇔ 2x(x + 1) = 0
QUẢNG CÁO⇒ x = 0; x = -1
+ Giao với Ox: (0; 0); (-1; 0)
+ Giao với Oy: (0; 0)
Số giao điểm của đồ thị hàm số y = x 3 − 2 x 2 + x + 1 với đường tiệm cận ngang của đồ thị hàm số y = x − 1 x + 1 là
A. 2
B. 3
C. 1
D. 0